3. Законы сохранения в современной физике

В конце 1900 г. М. Планк предложил свою знаменитую формулу для энергии спектра излучения абсолютно черного тела. До этого было известно две экспериментальные зависимости: в области малых частот было справедливо распределение Релея - Джинса, в области больших частот - распределение Вина. Планку удалось получить интерполяционное выражение для всей области спектра, содержащее в себе в соответствующих областях две крайние зависимости. При этом оказалось, что энергетическая зависимость не может быть непрерывной, а величина скачков энергии растет пропорционально соответствующей частоте. Роль коэффициента пропорциональности выполняла универсальная постоянная h, которая и была здесь впервые введена Планком. Так как размерность ее была энергия × время, то Планк назвал ее квантом действия (действие имеет как раз такую размерность).

Планк так говорил о своем результате: энергию системы осцилляторов, представляющих материальное тело, в равновесии с которым находится черное излучение, необходимо представлять не как непрерывную, неограниченно делимую величину, а как величину дискретную, состоящую из ряда конечных, равных между собой чисел.

Однако Планк не сразу пришел к пониманию смысла полученного им результата. Лишь после объяснения Эйнштейном законов фотоэффекта (1905) стал ясен подлинный смысл этого поистине великого открытия, явившегося первым толчком к развитию квантовой механики.

Эйнштейн постулирует, что всякая монохроматическая волна определенной частоты v несет с собой квант энергии, равный hv, и импульс ^hv/_c. Используя лишь это утверждение и применяя к фотоэффекту закон сохранения энергии он объясняет все характерные особенности этого явления. С этого времени возникает представление о дискретной структуре света, выражающееся в том, что каждой длине волны отвечают вполне определенные порции и энергии. Такая корпускулярная структура излучения отражается в понятии фотона или кванта - "элементарной" частицы света, соответствующей излучению данной длины волны. Столь же непринужденное объяснение с помощью теории световых квантов получили явления фосфоресценции и флюоресценции, фотохимических реакций, протекающих с поглощением света, а также ход теплоемкости твердых тел (теория Эйнштейна - Дебая) и поведение двухатомных газов вблизи абсолютного нуля.

Следующим этапом в развитии гипотезы световых квантов явилось объяснение Нильсом Бором в 1913 г. эмпирических законов линейных спектров. Он постулирует наличие стационарных электронных орбит в атоме: каждому состоянию электронов отвечает определенная энергия Е¹, E₂ и т. д. Находясь в движении на определенной орбите, электрон, как это было установлено, не может излучать (как этого требует классическая электродинамика). Зато при переходе с одной орбиты (уровня) на другую он испускает (или поглощает) световой квант, частота которого определяется уравнением hv = E₂ - E₁. Отбор стационарных орбит осуществляется на основании следующего квантового условия: момент количества движения электрона при его движении по орбите должен быть целым, кратным величине ^h/_2π = K. Несмотря на многие успехи этой концепции, уже в самом начале ее развития появились непримиримые противоречия, ставившие под вопрос ее справедливость. К 1924 г. ситуация настолько усложнилась и запуталась, что Бором, Крамерсом и Слеттером была предпринята попытка примирить боровскую теорию с классической путем отказа от представления о том, что волновое поле несет энергию. Предполагалось трактовать закон сохранения энергии статистически, т. е. принять, что в индивидуальных микроскопических актах поглощения или испускания света энергия не сохраняется, общий же баланс энергии выполняется в среднем как результат наложения случайных компенсаций. По существу, это был отказ от закона сохранения энергии как абсолютного закона природы вообще, а это означало полную утрату его положительной стороны - утверждения о превращении энергии из одной формы в другую.

В истории были и до этого факты непризнания справедливости закона сохранения энергии. Еще на первой стадии его развития, когда он завоевывал умы физиков, против него выступали яростные принципиальные противники (Пфафер, Зутер). Затем, после открытия радиоактивности, встал вопрос, откуда берется неисчерпаемая, казалось, способность радиоактивных веществ к испусканию излучения. Однако очень скоро (в 1902 г.) экспериментами Резерфорда и Содди было подтверждено сохранение энергии при радиоактивных превращениях. И вот теперь, после стольких успехов применения этого закона к самым различным элементарным процессам, снова ставилась под сомнение его справедливость. Даже открытие в 1923 г. эффекта Комптона и, как мы это уже показали, блестящее его объяснение Комптоном и Дебаем путем совместного применения релятивистских законов сохранения энергии и импульса с использованием гипотезы квантов не воздействовало на авторов статистической трактовки закона сохранения энергии.

Лишь экспериментальное подтверждение законов сохранения в отдельном акте комптоновского рассеяния, данное Бете и Гейгером (1925), а также Алихановым, положило конец этим сомнениям. Однако вопрос о сохранении энергии снова был поставлен под сомнение в результате работ Эллиса и Вустера (1927). Они установили, что спектр α- и γ-излучений ядер имеет дискретный характер, что указывало на дискретный характер уровней энергии ядер, но зато β-спектр является непрерывным, причем эта непрерывность первична. Если бы наряду с β-частицей испускалась вторая частица, все было бы ясно, так как выделяемая энергия распределялась бы произвольным образом между двумя частицами. Но никаких следов такой частицы не существовало. Тем не менее Паули в 1933 г . в докладе на седьмом Сольвеевском физическом съезде, основываясь на нерушимости закона сохранения и превращения энергии, делает смелое предположение о существовании новой частицы, которая, вылетая из ядра при β-распаде, уносит с собой определенную долю энергии, но ускользает от нашего наблюдения. Эта гипотеза, однако, многим физикам казались искусственной натяжкой, призванной спасти закон сохранения энергии, и рассматривалась как проявление консерватизма. Тогда с отказом от закона сохранения и превращения энергии выступает Н. Бор. Однако дальнейшие эксперименты Сержента показали, что энергия β-электрона имеет определенную верхнюю границу для каждого элемента, а также что эта максимальная энергия β-электрона равна разности уровней энергии атомных ядер до и после распада. Наконец, в 1934 г. Ферми предложил свою теорию р-распада, согласно которой вместе с электроном вылетает нейтральная частица с нулевой массой покоя, спин которой равен ¹/₂; это предположение диктовалось необходимостью соблюдения законов сохранения и превращения энергии и момента количества движения; было предложено называть новую частицу "нейтрино". Предположение о нулевой (или близкой к нулю) массе нейтрино непосредственно следовало из результатов опытов Эллиса и Мотта. С этого времени начинается серия экспериментов по доказательству существования нейтрино. Советский физик А. И. Лейпунский поставил в 1936 г. в Кембридже (Англия) первую экспериментальную работу по излучению импульса нейтрино в момент β-распада. Результаты его исследований имели качественный характер. Более доступным эксперименту было наблюдение отдачи в обратном β-процессе, когда ближайший к ядру электрон атома поглощается ядром; при этом испускается нейтрино и по закону сохранения импульса ядро испытывает отдачу (К-захват). Такие опыты на легких элементах были поставлены Алленом и затем Алихановым. Они дали новое подтверждение гипотезе нейтрино. Однако получить окончательное доказательство реального существования такой частицы оказалось возможным лишь после того, как были созданы достаточно мощные реакторы, дающие заметные потоки нейтрино (точнее, антинейтрино) благодаря радиоактивному распаду осколков деления. Если нейтрино существует, то должен наблюдаться процесс поглощения его протоном с образованием нейтрона и позитрона, причем последний, объединяясь с электроном, превращается в два фотона с энергией ~511 КэВ. Если нейтрино нет, такой процесс не должен наблюдаться. Проведенные Рейнесом и Коуэном в 1953 г., а затем в 1956 г. еще более тщательные эксперименты подтвердили реальность этого процесса. Тем самым было дано прямое доказательство существования нейтрино - наиболее "неуловимой" из всех элементарных частиц.

Можно привести и другие примеры, свидетельствующие об успешном применении законов сохранения к микропроцессам. Например, совместное применение закона сохранения энергии и импульса к распаду частицы на две новые приводит к утверждению, что во всех случаях каждый из продуктов распада должен обладать одной и той же энергией. Когда оказалось, что в разных актах распада мю-мезона на электрон и нейтральную частицу энергия электрона разная, пришлось принять, что наряду с электроном образуется два нейтрино. Это следовало также и из закона сохранения момента: все три частицы имеют спин ¹/₂. При распаде на электрон и одно нейтрино момент системы превращался бы из полуцелого в целый, что невозможно. Так была установлена схема распада.

Попытки объяснить явления микромира при помощи классической механики и электродинамики приводили к противоречию с действительностью. Необходимо было создать новую теорию, которая бы более точно и полно охватывала известные опытные факты, предсказывала новые эффекты и тем самым толкала бы физиков на дальнейшие поиски. Такая теория - теория квант - была создана, и она помогла ученым отрешиться от многих привычных представлений классической физики. Свойственное метафизическому образу мышления решение вопроса: "да - да", "нет - нет" находило в классической физике свое отражение в противопоставлении прерывного и непрерывного, волн и корпускул и т. д.

Новые факты, полученные в результате изучения микромира, требовали применения диалектического метода для своего теоретического обобщения. В микромире нельзя было уже пользоваться грубомодельными представлениями классической физики - здесь наиболее ярко проявляются противоречивый характер явлений, взаимосвязь и взаимовлияние, обнаруживаются новые свойства, для осмысления которых надо вводить понятия, не имеющие аналогов в классической физике.

Создание теорий микропроцессов проходило на базе новых экспериментальных данных и основных законов, прежде всего законов сохранения классической физики, содержание которых в квантовой механике было обогащено, а форма претерпела изменения. Следует подчеркнуть, что это произошло потому, что микромир отличается от макромира не только количественными, но и качественными характеристиками. Ему присущи такие свойства и качества, которые в макромире не существуют.

А. Законы сохранения энергии, импульса, момента импульса

Рассмотрим вопрос о том, как формулируется закон сохранения энергии в квантовой механике. Система в состоянии

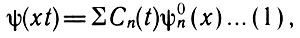
где

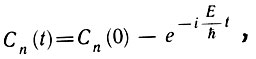
в каждый данный момент может обладать любым из возможных значений энергии Еп- Допустим, система изолирована или находится в постоянных внешних условиях, т. е. Н (оператор Гамильтона) не зависит от времени явно. Тогда

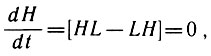
следовательно, Е = const. Это видно и непосредственно из (1), написанного как раз для замкнутой системы.

Итак, закон сохранения энергии в квантовой механике формулируется следующим образом: вероятность найти определенное значение энергии Еп замкнутой системы не зависит от времени.

Хотя в каждый данный момент энергия системы принимает любое из возможных значений (каждое со своей вероятностью), средняя по квантовым состояниям энергия остается постоянной.

Но система может находиться и в стационарном состоянии ψ(xt), тогда во все моменты времени она будет обладать определенной энергией Е_n. В этом случае даже некоммутирующие с Н величины будут иметь постоянные во времени средние значения (если только соответствующий оператор не зависит явно от времени). Энергетический спектр может быть как непрерывным (свободное состояние), так и дискретным (связанное состояние). Далее, как и в классической механике, для изолированной системы должны выполняться законы сохранения импульса и момента. Если при этом исходят из теоремы Нетер, то автоматически получаются выражения для операторов того и другого (69, 59-104).

Собственными функциями оператора импульса являются

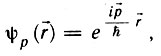
спектр его собственных значений непрерывный. Состояния с определенным импульсом являются свободными состояниями.

Момент количества движения L в единицах 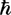может принимать лишь целочисленные значения; собственное значение оператора квадрата момента равно

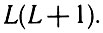
В силу неперестановочности операторов проекций момента на Декартовы оси координат имеет смысл говорить как об определенных величинах лишь о квадрате момента и одной из его проекций (или двух проекциях). Проекция момента на любую выделенную ось принимает

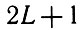
число значений. В отсутствии выделенного направления (т. е. когда нет, например, магнитного поля) все эти

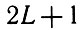
состояния системы обладают одной и той же энергией, т. е. являются вырожденными. Наложение поля снимает это вырождение-состояния различных проекций момента становятся отличными и по энергии.

Кроме этого так называемого орбитального момента, вводится понятие, не имеющее себе аналога в классической механике,- спин, или собственный момент количества движения частицы.

В силу принципа тождественности частиц волновая функция системы одинаковых частиц должна быть либо симметричной, либо антисимметричной относительно перестановки любой пары частиц. Первая возможность осуществляется для бозонов, вторая - для фермионов.

Закон сохранения момента должен формулироваться с учетом также и спинов частиц, входящих в систему. При этом в случае фермионов появляется следующий запрет: при всех превращениях в системе полное число фермионов не может измениться от нечетного к четному, и наоборот, или короче: полное число фермионов, oучаствующих в реакции, должно быть четным. (Примером этому - распад (μ→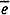 + v + )

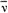Наличие сохраняющихся величин в квантовой механике имеет для нее огромное принципиальное значение. Именно благодаря этим величинам оказывается возможным полное описание квантово-механических систем. Определенные их комбинации могут представлять собой так называемые полные наборы величин, с помощью которых производится классификация состояний. В этой связи сохраняющиеся величины в квантовой механике называют "хорошими" квантовыми числами.

Но квантовая механика внесла новое не только в понимание уже известных законов сохранения. Она привела к открытию новых сохраняющихся величин, причем во всех случаях факт сохранения определенной величины связан с существованием определенной симметрии системы.

Сами факты сохранения (исключение составляет пока принцип четности) в квантовой механике носят характерную форму запретов, накладываемых на состояния и процессы. Все эти особенности квантовых законов сохранения лучше всего разобрать последовательно на каждом из них.

Б. Закон сохранения четности

Однородность и изотропность пространства может быть установлена преобразованием инверсии. Если при изменении знаков всех координат физическое состояние системы не меняется (т. е. она описывается прежним гамильтонианом), то ее пространство однородно и изотропно. В классической механике этому преобразованию не соответствовал никакой интеграл движения, так как оно не является непрерывным и потому не может быть сделано бесконечно малым.

Зато в квантовой механике ему отвечает понятие четности и сохранения ее для замкнутой системы или системы, находящейся в центрально-симметричном поле. Действие оператора четности P на волновую функцию ψ состоит в замене 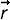→-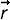. Так как двукратное применение оператора четности Р2 есть тождественное преобразование, то собственными значениями будут являться +1 и -1, т. е. его собственными функциями в первом случае будут любые четные ψ, .во втором - любые нечетные ψ.

Поскольку оператор четности и операторы момента и его проекций коммутируют между собой, то соответствующие величины имеют одновременно определенные значения. Более того, существует связь между четностью и моментом состояния орбитального движения отдельной частицы

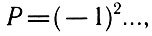
причем состояние с различными проекциями момента L имеет одну и ту же четность.

Итак, закон сохранения четности имеет место, если

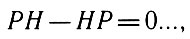
и состоит в следующем: если состояние замкнутой системы обладает определенной четностью, то эта четность сохраняется.

В случае двух одинаковых частиц операция инверсии тождественна с их перестановками: если это бозоны с нулевым спином, их волновая функция должна быть симметричной, а согласно (2) должны быть четными и моменты. Таким образом, на состояние системы двух бозонов налагаются запреты: разрешенными являются лишь четные состояния с четными моментами.

В частности, исходя из существования ядерной реакции

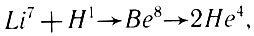
происходящей через промежуточное ядро бериллия с испусканием двух α-частиц (спин - нуль), можно сделать заключение о том, что энергетические уровни промежуточного ядра характеризуются квантовыми числами момента и четности: 0⁺, 2⁺ , 4⁺ и т. д.

Так, совместное применение законов сохранения четности и момента помогает при экспериментальном определении спинов и четности в основном и в возбужденном состояниях.

Дальнейшее развитие принципа четности в применении к процессам, происходящим с нуклонами, π-мезонами и другими элементарными частицами, привело к необходимости введения понятия внутренней четности частицы. Это свойство определяется поведением волновой функции частицы при инверсии относительно начала системы координат, связанной с частицей (т. е. в системе ее покоя). Понятие внутренней четности не имеет смысла для частиц с массой покоя, равной нулю (фотон, нейтрино). Кроме того, в действительности можно определить внутреннюю четность данной частицы лишь в отношении к внутренней четности другой частицы. Так, Пановским установлено, что четность π-мезона противоположна четности протона. Если считать, что четность протона положительна, то это означает, что π-мезон является псевдоскалярной частицей (имеет отрицательную четность).

Все эксперименты в области ядерных и электромагнитных взаимодействий свидетельствовали о строгом выполнении закона сохранения четности.

Среди слабых взаимодействий лучше всего исследован ^-распад, и накопившиеся к 1956 г. экспериментальные данные также не давали повода сомневаться в строгом соблюдении принципа четности. Однако позже были получены сведения, упорно заставлявшие задуматься над тем, действительно ли четность сохраняется. В самом деле, оказалось, что все K-мезоны, считавшиеся ранее различными в силу различия в способах распада, имеют одинаковые, в пределах ошибок эксперимента, массы. В частности, это относилось к θ- и τ-мезонам, которые распадаются по схемам:

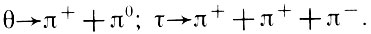
Так как π-мезон имеет отрицательную внутреннюю четность, первому случаю отвечают возможные состояния 0⁺ , 1^-, 2⁺ , а второму О^-, 1⁺, 1^-, 2⁺ , 2^-; причем наиболее вероятными значениями спина и четности τ-частицы являются 0^- и 2^-.

Таким образом, возникает дилемма: либо четность не нарушается и это разные частицы, что противоречит экспериментальному факту равенства их масс, либо это одинаковые частицы и тогда четность не сохраняется, что противоречит привычным представлениям, выработанным на протяжении всего хода развития теоретической физики. Поэтому высказывались сомнения относительно точности обсуждаемых экспериментов. Тем временем теоретиками Ли Цзундао и Янг Чженьнин, работавшими в США, была предложена смелая гипотеза, согласно которой в слабых взаимодействиях закон сохранения четности не выполняется. Исходя из этого общего положения они указывали конкретные эффекты из области β-распада, распада мезонов и гиперонов, которые могли бы дать прямое подтверждение или опровержение этой гипотезы.

Поставленный группой By эксперимент с β-распадом ориентированных ядер кобальта подтвердил несохранение четности. Асимметрия π→μ→е-распада, наблюдаемая группой Ледермана, указывала на несохранение четности в этом случае. Последующие многочисленные эксперименты также подтвердили гипотезу Ли и Янга.

Однако простой отказ от принципа четности противоречил фундаментальным представлениям о свойствах пространства, его изотропности, проявляющейся в строгом выполнении закона сохранения момента. Закон зеркальной симметрии говорит о том, что для мира, отраженного в зеркале, действительны те же законы. Однако это очевидное положение оказалось верным только приближенно. Выход из создавшейся ситуации был впервые предложен академиком Л. Д. Ландау (52, 406). Независимо от него к аналогичным результатам пришли Ли и Янг.

Л. Д. Ландау пришел к выводу, что слабые взаимодействия нарушают не только сохранение четности, но и симметрию частиц и античастиц, которая приводит к строгому закону сохранения в случае сильных взаимодействий; зато им постулировалась инвариантность законов природы относительно комбинации обоих преобразований, которая была названа комбинированной инверсией. Ниже мы рассмотрим этот вопрос более подробно.

В связи с экспериментальным подтверждением несохранения четности возникает интересный вопрос - о научной смелости при истолковании получаемых результатов и о сковывающем влиянии существующих теорий. Подчеркивая огромное эвристическое значение законов сохранения, следует тем не менее обратить внимание и на наличие отрицательной стороны в безоговорочном признании абсолютности и основополагающего значения всех законов сохранения в их конкретной, исторически ограниченной форме.

При использовании законов сохранения для новых выводов всегда следует тщательно разобраться в конкретной обстановке эксперимента и к новым результатам подходить как к возможным сигналам о том, что уже нарушена граница применимости данного закона. Известный английский физик-экспериментатор Блэкетт говорил по этому поводу, что несохранение четности могло быть обнаружено за тридцать лет до 1956-1957 гг. Еще в опытах Кокса и Чейса в 1928-1930 гг. было достаточно убедительно показано, что β-частицы продольно поляризованы. Блэкетт также замечает, что слабая асимметрия распределения электронов в π→μ→e^- распаде была замечена уже давно. Из рассмотрения этих исторических фактов автор приходит к выводу, что экспериментаторы слишком часто воздерживались от простых и важных опытов только потому, что эти опыты не имели смысла с точки зрения теории, существовавшей в то время. Если бы у них хватило смелости на такие опыты, они поняли бы, что в данном случае общепринятые принципы теории не имеют глубокого обоснования. Рассматривая успехи в развитии теории β-распада, следует подчеркнуть, что выдающийся успех в этой области объясняется не только прогрессом в развитии экспериментальной техники, но и тем влиянием, которое оказал на умы и руки исследователей факт нарушения одного из основных законов сохранения. Во всяком случае, глубокий, творческий, критический подход к существующей теории и к получаемым новым экспериментальным данным, диалектическое сочетание теории и практики - единственно верный путь дальнейшего познания природы.

В. Зарядовое сопряжение. Закон сохранения зарядовой четности

Рассмотренные законы сохранения энергии, импульса, момента и четности непосредственно связаны со свойствами симметрии пространства и времени, выражающимися в их однородности и изотропности.

Пространственные и временные свойства материальных объектов являются наиболее общими, и потому так велико значение упомянутых законов в познании материальных процессов и структуры фрагмента материи, изучаемого физикой. Однако в природе существуют и внутренние симметрии взаимодействия. Соответствующие им законы сохранения отражают внутренние свойства этих объектов, их природу. Таковы зарядовая симметрия и изотопическая инвариантность.

Впервые представление о зарядовом сопряжении (зарядовой симметрии) возникло при рассмотрении уравнения Дирака. Из него следовала необходимость существования состояний электронов с отрицательной энергией.

Первоначально Дирак предложил следующее объяснение: если электрон с отрицательной энергией получит достаточную энергию, он переходит в состояние с положительной энергией. Оставшаяся "дырка" в дираковском фоне ведет себя как частица с массой, равной массе электрона, но с противоположным зарядом. Таким образом, возникают две частицы, различающиеся по знаку заряда и способные снова исчезать при взаимной "аннигиляции"¹ (электрон заполняет "дырку"), выделяя соответствующие количества энергии. Так в своеобразной теоретической форме было предсказано существование наряду с частицами их античастиц, способных совместно рождаться и уничтожаться, хотя сам Дирак имел в виду не положительный электрон, а протон. Поскольку в период создания им релятивистской теории электрона единственной известной и наблюдаемой элементарной частицей (с положительным зарядом) был протон, Дирак и отождествлял свой положительный электрон с протоном, хотя он почти в 2000 раз тяжелее электрона. Выход из создавшегося противоречия искали в конструировании различных связей и процессов, которые должны были разъяснить эту разницу в массах.

¹ (Когда частица и античастица взаимодействуют друг с другом, кинетическая энергия и масса покоя двух частиц преобразуются в кванты соответствующих полей. Этот процесс физики назвали аннигиляцией, но, строго говоря, данный термин в философском плане неудачен, ибо первоначальный его смысл - это уничтожение, исчезновение (annihilation). В идеалистической философии он используется для обозначения исчезновения.)

Теория Дирака содержала в себе такие возможности, которые на первом этапе не смог понять даже сам ее создатель. Но ее появление открывало перед экспериментаторами новые пути и их поиск увенчался успехом.

В скором времени Андерсоном (1932) в космических лучах действительно была открыта новая частица - позитрон, или электрон с положительным знаком заряда. Это открытие явилось триумфом научного теоретического предвидения. Оно означало, что уравнение Дирака не только правильно описывает поведение электронов, но также и отражает существенное свойство симметрии природы: каждой частице должна соответствовать ее античастица; так, протону должен отвечать антипротон, нейтрону - антинейтрон и т. д.

Обнаружение в 1955 г. (Сегре и другие) антипротона, а затем и антинейтрона означало новый успех теории; теперь уже никто не сомневался, что на новых мощных ускорителях будут обнаружены и антигипероны. Вскоре они были открыты.

Дальнейшее теоретическое осмысление свойств симметрии в природе, существование симметрии частиц - античастиц привело к необходимости ввести новое понятие зарядовой сопряженности- "мыслимое" преобразование, при котором все частицы заменяются на античастицы, а античастицы заменяются на частицы, так что все электрические заряды и магнитные моменты, а также электромагнитные поля меняют знак. При этом уравнения, описывающие движение системы, должны быть инвариантны относительного зарядового сопряжения. В частности, должны быть равны по величине заряды и массы частицы и античастицы, атомные спины и магнитные моменты.

Экспериментально это подтверждено с достаточной степенью точности (например, для пар е⁺-е^-, μ⁺-μ^-, π⁺-π^-).

На примере бозонов π⁺ и π^- ясно видно, что представление о дираковском фоне должно быть оставлено, так как для них принцип Паули не применим.

Поведение системы из частиц и античастиц отображается теорией вторичного квантования с ее операторами рождения и поглощения частицы или античастицы. Античастица вводится как частица, зарядово сопряженная собственно частице. Основное свойство античастицы - способность к "аннигиляции" с частицей. Отсюда вытекает техническое правило при написании реакций с частицами - каждую из них можно переносить в другую сторону равенства, заменяя на античастицу.

Незаряженные частицы, переходящие при зарядовом сопряжении сами в себя, называются истинно нейтральными (γ, π°).

Существуют нейтральные частицы, которые ведут себя подобно заряженным: они имеют античастицы, отличные от них самих. Например, нейтрино и антинейтрино, нейтрон и антинейтрон отличаются направлением магнитного момента относительно спина; к этой же группе относятся нейтральные гипероны.

Дважды произведенная операция зарядового сопряжения возвращает систему в прежнее состояние, т. е. С²=+1, откуда следует собственное значение оператора С:+1 и - 1. Поэтому для нейтральных частиц можно ввести понятие зарядовой четности (к заряженным частицам оно не применимо, так как при операции С они превращаются в античастицы).

Зарядовая симметрия означает инвариантность гамильтониана относительно С, откуда следует, что H и С коммутируют, значит, собственные значения оператора являются интегралами движения, т. е. зарядовая четность нейтральной системы сохраняется (186, 138).

Так как электромагнитное поле меняет знак при операции зарядового сопряжения, то уквант есть зарядово-нечетная частица; π°-мезон, распадающийся на два фотона, зарядово-четен. Произвольная нейтральная система, имеющая определенную зарядовую четность, может распадаться только на четное число фотонов (аннигиляция орто- и парапозитрония). По нашему мнению, название "зарядовая четность" неудачно, так как может ввести в заблуждение, создать впечатление, что оно относится к заряженным частицам, в то время как это понятие имеет смысл лишь для нейтральных частиц. Исторически сложившийся термин "зарядовое сопряжение" также неудачен; может, например, показаться с первого взгляда, что ∑⁺ и ∑^--гипероны являются частицей и античастицей одновременно; однако это не так. Действительно, распад ∑^-, например, происходит согласно схеме

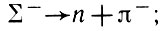
процесс, зарядово сопряженный этому распаду, будет

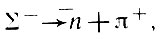
в то время как ∑⁺ распадается двумя способами, отличными от последнего:

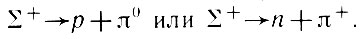
Поэтому для каждого из ∑-гиперонов имеется свой антигиперон (конечно, имеющий противоположный знак заряда).

Здесь мы впервые встречаемся с непривычным случаем, когда две частицы с практически (но не точно!) равнымми массами и с противоположными электрическими зарядами не находятся в отношении частицы/античастицы друг к другу. По аналогии с протоном и нейтроном Маршак и Зэдерман высказали предположение о том, что различие в массах ∑-гиперонов - следствие различия их аномальных магнитных моментов.

Итак, инвариантность относительно зарядового сопряжения имеет место как в электромагнитных, так и в сильных взаимодействиях. Ландау (52, 406) предположил, что для слабых взаимодействий она несправедлива, как и сохранение четности, зато имеется инвариантность по отношению к одновременной операции инверсии и замены частицы на античастицу (и наоборот) - так называемой комбинированной инверсии. При этом пространство остается полностью симметричным, асимметричными же являются электрические заряды. "Эта асимметрия в такой же мере не затрагивает симметрии пространства, как ее не затрагивает существование химической стереоизометрии.

С другой стороны, у заряженных частиц не возникает никакого закона сохранения четности, так как оператор комбинированной инверсии не переводит заряженные частицы сами в себя" (52, 406).

При комбинированной инверсии сами в себя переходят истинно нейтральные частицы, так как для них комбинированная инверсия имеет характер обычной инверсии, поэтому сохранение четности для этих частиц имеет место при всех взаимодействиях (52, 406). Эта четность есть произведение обычной четности на зарядовую их четность, т. е. фотон в этом смысле нечетен, π°-мезон четен и т. д.

В итоге гипотеза комбинированной инверсии устраняет трудность с асимметричным пространством и переносит ответственность за эту асимметрию на заряды как на материальные ее носители. Эта привлекательная концепция получила многочисленные экспериментальные подтверждения.

Следует заметить, что предложение Ландау о комбинированной инверсии сохраняет наши первичные представления о пространственно-временном континууме, но оно не является единственно возможным объяснением полученных экспериментальных данных.

Закон сохранения четности и комбинированная инверсия имеют большое философское значение, как еще одно свидетельство противоречивой сущности материи и таких основных форм ее бытия, какими являются пространство и время.

Г. Закон сохранения барионного (ядерного) заряда. Лептонный заряд

Независимое от наблюдений и наблюдателей существование окружающего нас мира свидетельствует об относительной стабильности тяжелых частиц, хотя и известны факты спонтанного деления тяжелых ядер. Поскольку протон практически существует бесконечно долго (стабильность протона проверена с высокой степенью точности: для нижнего предела времени жизни протона получено значение ~ 10³² лет, что несравненно больше времени существования астрономической Вселенной).

Теперь, когда уже существует теория Великого объединения, вновь обсуждается вопрос о стабильности протона, так как она предсказывает его нестабильность, а значит, и несохранение барионного заряда. Расчеты показывают, что за время существования Вселенной могла распадаться только 10^-20 часть от общего числа протонов, и этот распад не изменяет наших представлений об их относительной неизменности.

Такая стабильность ядерной материи может быть истолкована как закон сохранения числа нуклонов. С учетом гиперонов и античастиц его можно сформулировать так: разность числа тяжелых частиц и числа соответствующих античастиц является константой движения. Впервые в применении к нуклонам и λ°-частице это положение было высказано Шиффом.

Независимо аналогичные соображения были развиты в общетеоретической форме японским физиком Онедой. Наконец, Зельдович предложил ввести понятие ядерного заряда аналогично электрическому. Протону и нейтрону приписывается ядерный заряд +1, антинуклонам -1, частицам с массой, меньше массы нуклона, - 0. Согласно известным схемам распада, получено, что гипероны и антигипероны имеют ядерные заряды соответственно +1 и -1. Так как общим названием двух групп элементарных частиц - нуклонов и гиперонов-является барион, то и закон сохранения называется законом сохранения барионного заряда.

Таким образом, сохранение числа частиц принимает совершенно простую наглядную форму: при всех взаимодействиях должен сохраняться полный барионный заряд замкнутой системы. Закон сохранения барионного заряда - результат процесса сильных взаимодействий.

В физике элементарных частиц "работает" и понятие лептон-ного заряда (+1 для е^-, μ^- и v и -1 для е⁺, μ⁺ и v_), характеризующее процессы слабых взаимодействий. Такая возможность обусловлена тем экспериментальным фактом, что нейтрино не является истинно нейтральной частицей, т. е. v и v_ - разные частицы (последние результаты по двойному β-распаду). В этом случае оказывается, что ц-распад происходит согласно схеме

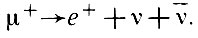
Наряду с понятиями электрического и барионного заряда вводится понятие лептонного заряда (L_e, L_μ, L_τ), сохраняющегося при всех превращениях¹. Выбирая естественным образом лептонный заряд электрона и мю-мезона, можно строго запретить ненаблюдаемые процессы типа

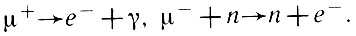
¹ (Закон сохранения лептонного заряда был впервые сформулирован Я. Б. Зельдовичем, Д. Марксом, Э. Кнопинским и Е. Махмудом.)

При операции зарядового сопряжения должны меняться знаки всех трех зарядов. Для барионного заряда это следует хотя бы из того факта, что не существует отрицательно заряженного нуклона с положительным барионным зарядом. Симметрия законов природы относительно зарядового сопряжения означает, следовательно, их симметрию относительно операции одновременного изменения знаков всех зарядов, т. е. в паре частица - античастица должны иметь противоположный знак не только электрические заряды, но и барионные и лептонные. К этому и сводится основное физическое различие частицы и античастицы, состоящее в их способности аннигилировать друг с другом. Тем самым сохранение барионного заряда непосредственно связано с возможностью полного освобождения энергии, соответствующей массе покоя.

В теории все три закона сохранения (электрического заряда, тяжелых частиц и легких частиц) являются следствием инвариантности лагранжиана поля относительно калибровочного преобразования. Они связаны с неизменностью уравнений при замене электромагнитных потенциалов на величины, отличающиеся либо постоянной, либо добавкой в виде градиента некоторой функции, так как в современной теории волновые функции поля входят билинейно в лагранжиан (в виде UU^*), преобразование волновой функции

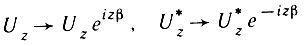
с произвольным р не должно приводить к новым физическим следствиям. Отсюда и вытекают строгие законы сохранения зарядов.

Следовательно, необходимо четко различать сохранение заряда как экспериментальный факт, более или менее надежно проверенный, и как теоретическое выражение , этого факта, форма которого может и должна изменяться в соответствии с изменением и совершенствованием математического аппарата, описывающего физические явления. В настоящее время закон сохранения электрического заряда представляется безоговорочно точным. Сохранение барионного заряда будет практически абсолютно точным, пока не будет обнаружено возможных в принципе процессов спонтанного распада тяжелых частиц на легкие.

Закон сохранения лептонного заряда был подвергнут экспериментальной проверке, которая с большой степенью точности подтвердила его истинность.

Математически все три закона вытекают из требования градиентной инвариантности любой теории и проявляют себя как правила отбора в возможных типах элементарных взаимодействий.

Три дискретных преобразования - преобразование зеркального отражения, преобразование зарядового сопряжения и преобразование отражения времени - связаны между собой важной теоремой, называемой СРТ теоремой.

Известно, что в квантовой теории поля вводятся различные операторы симметрии в Гильбертовом пространстве физических состояний. Рассмотрим три дискретных преобразования симметрии: пространственное отражение Р, отражение времени Т и зарядовое сопряжение С (точнее, замена частиц античастицами). Физический смысл этих преобразований состоит в следующем. Пространственное отражение Р: состояние частиц с пространственными координатами r_i, импульсами P_i и проекциями спинов σ_i (для спинов, отличных от нуля) преобразуется в состояние тех же частиц с координатами r_i, импульсами Р_i и прежними проекциями спинов σ_i. Отражение времени Т: состояние частиц с координатами r_i, импульсами - Р_i и проекциями спинов σ_i преобразуется в состояние тех же частиц с прежними координатами r_i, но с импульсами P_i и обратными по знаку проекциями спинов - σ_i. Кроме того, направление времени изменяется на обратное, т. е. падающие частицы заменяются уходящими частицами, и наоборот. Зарядовое сопряжение С: частицы преобразуются в соответствующие античастицы без изменения пространственных координат r_i, импульсов Р_i,- и спинов σ_i. Теорема СРТ гласит: локальная теория квантового поля, инвариантная относительно Лоренцовых вращений и включающая в себя обычную причинную коммутативность или антикоммутативность операторов поля, всегда инвариантна относительно произведения преобразований СРТ. Физически теорема СРТ, например, означает, что равны между собой вероятности перехода для следующих двух процессов: 1) в результате взаимодействия частиц в точках с координатами r_i, импульсами Р_i и спинами σ_i образуются частицы в точках с координатами r_i, импульсами Р_i и спинами σ_i 2) в результате взаимодействия соответствующих античастиц в точках с координатами r_i, импульсами Р_i и спинами σ_i образуются античастицы в точках с координатами r_i, импульсами Р_i и спинами σ_i.

Опыт показывает, что некоторые частицы встречаются в природе только в одной форме, тогда как для других известны два типа. Так, все нейтральные π°-мезоны идентичны, а заряженные π-мезоны могут иметь оба знака заряда. В последнем случае говорят о частицах и античастицах, хотя логически нельзя приписать частице свойство быть либо частицей, либо античастицей; можно лишь утверждать, что по отношению друг к другу эти две формы частиц являются античастицами.

Оправдание существования таких частиц связано не только с теоремой СРТ, но и с понятием обобщенного заряда. Под обобщенным зарядом понимают строго сохраняющееся аддитивное квантовое число, переносимое индивидуальными частицами. В природе, по-видимому, существуют такие обобщенные заряды:

1. Электрический заряд.
2. Лептонный заряд.
3. Барионный заряд.
4. Гиперзаряд: Y = S + B, где S - странность, а В - барионный заряд.

Электрический заряд играет особую роль, поскольку он не только является аддитивным квантовым числом, но также измеряет силу взаимодействия частиц с электромагнитным полем.

Исходя из принципа симметрии (теоремы СРТ и обобщенного заряда) Г. Людерс высказывает предположение: "По-видимому, для всех барионов существуют антибарионы; они должны характеризоваться (по меньшей мере) своим барионным зарядом. В пределах применимости сильных и электромагнитных взаимодействий существуют также пары частица - античастица, характеризуемые только нулевой странностью, а именно пара К₀, К₀_ (201, 313).

К началу 1957 г. единственной экспериментальной задачей, связанной с преобразованиями симметрии, было определение внутренних четностей, а для строго нейтральных частиц - также зарядовых четностей. Работы Ли и Янга открыли новую область экспериментальных проблем, связанных с эмпирическим определением инвариантности или неинвариантности относительно отдельных преобразований симметрии. Теорема СРТ входит в класс этих проблем. Если одно из трех свойств симметрии Т, С или Р нарушается (как это очевидно для Р в слабых взаимодействиях), то, по крайней мере, нарушается еще одно. Эмпирически представляется очевидным, что нарушается также С; имеются данные, которые могут свидетельствовать и o нарушении Т.

Д. Изотопическая инвариантность. Сохранение изотопического спина

Одним из важных законов сохранения, отражающим свойства симметрии материального объекта, является закон сохранения изотопического спина.

Нейтрон и протон являются частицами, очень похожими друг на друга: малая разница в массах, равенство спинов наталкивают на мысль о возможности рассмотрения их как различных состояний одной частицы. Почти сразу после открытия нейтрона и предложения Д. И. Иваненко протон-нейтронной модели ядра Гейзенберг ввел новую степень свободы для описания нейтрона и протона - зарядовую переменную, принимающую два значения соответственно двум состояниям нуклона: незаряженному (нейтрон) и заряженному (протон). Это была довольно привлекательная идея, однако она еще не имела под собой достаточных физических оснований. Далее было замечено большое сходство в свойствах так называемых зеркальных ядер, каждое из которых переходит в другое при замене нейтронов на протоны и протонов на нейтроны. Наконец, в опытах по рассеянию нуклонов было обнаружено, что ядерные силы между нуклонами (р-n, р-р, n-n) при малых энергиях приблизительно одинаковы для состояний с равными моментами и четностями. Это указывало на существование определенных свойств симметрии ядерных сил.

В 1936 г. Брейт и Финберг выдвинули гипотезу зарядовой независимости, согласно которой взаимодействие системы двух нуклонов зависит не от заряда, а только от момента и четности состояния. Другими словами, при изучении ядерных взаимодействий можно отвлечься от кулоновских сил. Отсюда следовало, что должны существовать два заряженных и один нейтральный кванты ядерного поля: π⁺ , π^-, π⁰.

Ферми предложил распространить гипотезу зарядовой независимости и на π-мезоны.

Поскольку зарядовая переменная Гейзенберга аналогично спиновой переменной принимает конечное число дискретных значений (два для нуклонов, три для π-мезонов), то можно ввести понятие изотопического спина, аналогично оператору обычного спина. Новый оператор действует на зарядовую переменную и обладает свойствами обычного момента количества движения. В частности, так как число проекций момента I равно 2I+ 1 и каждому зарядовому состоянию соответствует определенная проекция изотопического момента I, для нуклона должно быть I=¹/₂, для π-мезона I=1. Проекция этих моментов на произвольную ось Z изотопического пространства (пространство зарядовой переменной) будет -¹/₂ и +¹/₂, -1,0 и +1, каждый из которых соответствует n, р, π^-, л-π°, π⁺ .

Закон сохранения электрического заряда выражается теперь в факте строгого сохранения L (например, р→n+π⁺. Математическим выражением факта зарядовой независимости ядерных взаимодействий является сохранение полного изотопического спина, или изотопическая инвариантность. Это означает, что лагранжиан взаимодействия должен быть инвариантен относительно вращения в трехмерном изотопическом пространстве.

Однако сохранение I строго соблюдается лишь в процессах сильных взаимодействий. При электромагнитном взаимодействии полный изотопический спин уже не является хорошим квантовым числом, так как электромагнитное поле по-разному взаимодействует с зарядами разных знаков. Зато, как и в сильных взаимодействиях, при электромагнитных процессах сохраняется I_z.

Электромагнитное взаимодействие приводит к установлению различия в массах среди частиц с общим I. Так, с точки зрения существования одних сильных взаимодействий массы пир равны, также равны и массы π^-, π°, π⁺ (вырождение по I_z). "Включение" кулоновских взаимодействий снимает это вырождение; причем возникающее относительное различие масс по порядку величины равно отношению констант сильного и электромагнитного взаимодействий, т. е. ∞ ¹/₁₃₇. Распространение концепции изотопической инвариантности на гипероны и K-мезоны (Гелл-Манн, Нишиджима и др.) привело к первой удачной попытке классификации элементарных частиц (120). Что касается легких частиц (μ, e, γ, v), то к ним понятие изотопического спина еще широко не применяется.

Для нуклона и π-мезонов связь между электрическим зарядом Q (в единицах е) и I_z определяется соотношением

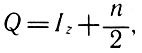
где n - ядерный заряд (в применении к системе частиц п есть разность между числом частиц и античастиц).

Следует обратить внимание на то, что основные положения теории изотопического пространства еще не ясны. У теоретиков даже нет единого мнения по поводу того, трехмерно или многомерно это пространство и в какой связи оно находится с обычным трехмерным пространством. Несмотря на такие пробелы в теории, она уже работает, так как, очевидно, относительно адекватно отражает объективную реальность, в абстрактной форме отображает новые черты, характеризующие элементарные частицы и их взаимодействия.

Е. Закон сохранения странности

На первой стадии изучения гиперонов и /(-мезонов физики столкнулись с поразительным фактом: в то время как эти частицы рождались в процессах сильных взаимодействий, т. е. за время порядка 10^-23 с, время их жизни составляло от 10^-10 до 10^-8 с. Это противоречило фундаментальному принципу обратимости: частица, образующаяся при сильных взаимодействиях, должна и уничтожаться в таких же процессах, т. е. за время порядка 10^-23 с. Именно поэтому K-мезоны и гипероны получили название странных частиц.

Строгий анализ ситуации позволил Пайсу и другим высказать предположение о том, что рождение странных частиц происходит парами или в большем числе. Сильные процессы такого рода не могут быть обратимыми, поскольку обратный процесс нарушил бы закон сохранения энергии. Например, из существования реакции парного рождения

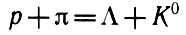
вытекает возможность,распада Л благодаря сильному взаимодействию в обратном процессе

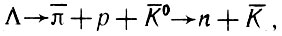
так как сумма масс продуктов такого распада больше массы распадающихся частиц. И действительно, исследования подтвердили факт совместного рождения. При этом обнаружилось, что возможны не всякие способы совместного рождения. Так, не было обнаружено процессов типа

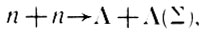
которые вполне совместимы с известными законами сохранения.

Гипероны рождались всегда в паре с K-мезонами. Кроме того, К⁺- и К^--мезоны вели себя по-разному при взаимодействии с нуклонами и при рождении.

Надо было объяснить не только факт парного рождения, но и все конкретные особенности этого процесса. Как говорят Гелл-Манн и Розенбаум, "когда природа исключает какое-либо явление, ее предписание часто принимает форму какого-нибудь закона сохранения" (147. 1958. 64(3), 391).

Самым замечательным явилось то, что для формулирования нового закона сохранения, объяснявшего все особенности поведения тяжелых частиц и К-мезонов, а также дававшего возможность определенных предсказаний, оказалось достаточным воспользоваться уже известными понятиями, и в первую очередь понятием изотопического спина. Каждой частице приписывается определенное значение нового квантового числа-странности S, которое является линейной комбинацией электрического заряда частицы ее нуклон-ного заряда и проекции изотопического спина:

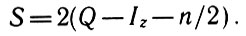
Для нуклонов и π^--мезонов оно равно нулю. Остальные частицы относятся к "смещенным зарядовым мультиплетам". Так, λ⁰ представляет изотопический синглет со странностью

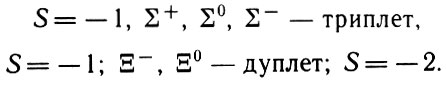
K-мезоны группируются в два разных дублета:

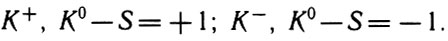
Вследствие сохранения Q, I_z, и n, S также должны сохраняться в сильных взаимодействиях.

Из определения S видно, что при переходе от частицы к античастице S меняет знак. В применении к K-мезонам это означало, что К⁰ и К⁰_, как К⁺, К^-, принципиально различны. Для таких нейтральных частиц требование сохранения странности и зарядовой четности приводило к весьма своеобразным квантовым эффектам, в частности предсказывалось существование наряду с известным тогда K°-мезоном другого K⁰_z_-мезона, который и был потом обнаружен экспериментально (K⁰₁ и K⁰₂).

Впоследствии на основании законов сохранения энергии и комбинированной четности было показано, что распад К⁰₁- и K⁰₂-мезонов должен идти по вполне определенным схемам. Однако в июле 1964 г. Кристенсон, Кронин, Фитч и Турлей (США) опубликовали работу (211, 138), где подчеркивали, что наблюдается реакция распада

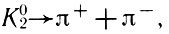
строго запрещенная в соответствии с вышеназванными законами сохранения (разрешенной является реакция К⁰₂_→π⁺+π^-+π⁰). Из 22 тыс. случаев распада K⁰₂-мезонов, наблюдавшихся авторами, в 45 случаях были обнаружены распады на два пиона. Ряд ученых в связи с этими открытиями заявляет о наличии нарушения закона комбинированной четности (СР-инвариантности, где С - изменение знака заряда, а Р - переход из правой системы в левую, и наоборот).

Чтобы спасти этот закон, играющий очень важную роль в теории элементарных частиц, была предложена гипотеза "пятой силы". Эта сила, очень слабая в наших условиях (по сравнению с сильным и даже гравитационным взаимодействиями), должна была играть существенную роль в масштабах космоса.

Предполагали, что эта асимметричная сила (ее знак противоположен для вещества и антивещества) превращает K⁰₂ в K⁰₁, который уже может распадаться на два π-мезона, без. нарушения закона сохранения комбинированной четности. Опыты, проведенные в Швейцарии (Церн) и Англии (Харуэлл), показали, что вероятность распада на два π-мезона не меняется с изменением энергии K⁰₂, как это должно было бы иметь место, если бы K⁰₂-мезон превращался в К⁰₁(пропорционально квадрату энергии). А раз это так, то гипотеза "пятой силы" не получила необходимого подтверждения. Отсюда делают вывод, что открытый необычный распад связан с нарушением закона сохранения комбинированной, а следовательно, и временной четности, что должно иметь далеко идущие последствия для теоретической физики.

Схема Гелл-Манна и Нишиджимы не только удовлетворительно объясняла многие экспериментальные результаты, но также и предсказывала существование новых частиц. Так, в период создания систематики Гелл-Манна не было известно, существуют ли ∑⁰ и Ξ⁰. Со временем были обнаружены обе частицы. Причем распад Ξ⁰ происходил на два K-мезона, как это вытекало из закона сохранения странности.

Из этого же принципа следует, что процесс

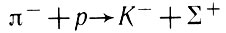
невозможен, в то время как может идти реакция

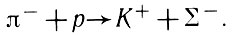
Наконец, если ограничиться однозаряженными частицами, схема смещенных изотопических мультиплетов допускает существование лишь четырех частиц: двух гиперонов и двух мезонов.

Гипотеза изотопической инвариантности приводит к определенным соотношениям между поперечными сечениями различных процессов, что дает дополнительный способ ее экспериментальной проверки.

Законы сохранения изотопического спина, барионного заряда и странности являются фундаментальными законами сильного взаимодействия. Для полной характеристики частицы относительно сильного взаимодействия вводится еще одно квантовое число - гиперонный заряд Y = S + B. Выбор гиперзаряда в качестве одного из основных квантовых чисел объясняется чисто формальными соображениями (например, гиперзаряд, подобно электрическому заряду, имеет целочисленные значения +1,-1,0). Закон сохранения, соответствующий гиперзаряду, нарушается при слабом взаимодействии.

С помощью формализма изотопического спина описываются основные свойства симметрии элементарных частиц, обусловленные их специфической структурой. Законы сохранения, связанные с перечисленными выше формами симметрии, дают основание предполагать у элементарных частиц динамически устойчивую структуру, которая сохраняется в своих основных чертах в процессе взаимодействия частиц. Вместе с тем нарушение данных законов сохранения при определенных взаимодействиях указывает на наличие некоторой асимметрии в свойствах и структуре элементарных частиц. Внутренние свойства микрочастиц (изоспин, барионный заряд, странность, гиперзаряд), на наш взгляд, отражают диалектическое единство моментов симметрии и асимметрии в микромире. Это проявляется прежде всего в том, что свойства частиц не только связаны с определенными формами симметрии, но и выражают специфику, различия в структуре микрообъектов. Так, например, странность и гиперзаряд описывают известную тождественность, симметрию в свойствах сильно взаимодействующих частиц, но они же указывают и на специфику этих частиц, что позволяет выделить данные частицы в особый класс. Это же относится и к изотопическому спину. Изоспин описывает симметрию зарядовой независимости и вместе с тем указывает на специфику сильного взаимодействия, на его отличие от других типов взаимодействий. Всякие же различия свидетельствуют о той или иной асимметрии; в этом смысле асимметрия определяет качественную специфику объектов, а симметрия обусловливает ее устойчивость. Единство симметрии и асимметрии, которое находит свое выражение в свойствах элементарных частиц, особенно наглядно обнаруживается во взаимодействиях. Асимметрия обусловливает динамику взаимодействия, возникновение качественно новых микрочастиц; симметрия же определяет сохранение, стабильность тех или иных свойств частиц в процессе взаимодействия. Специфические законы сохранения и превращения, которые управляют взаимодействием элементарных частиц, отражают это единство симметрии и асимметрии. Такими законами, в частности, являются законы сохранения и превращения барионного заряда, гиперонного заряда, странности и изотопического спина.

Уровень современных знаний еще не позволяет точно определить соотношение элементов симметрии и асимметрии в структуре микрообъектов, но уже сейчас очевидно их наличие в рамках одного структурного образования. Открытие новых форм симметрии и асимметрии и соответствующих им законов сохранения и превращения обогащает наши знания о структуре элементарных частиц, причем наряду с симметричностью структуры все более отчетливо обнаруживаются черты ее асимметричности. В этом проявляется диалектическая противоречивость структуры, ее большая динамичность, что, в частности, и обусловливает одно из основных свойств элементарных частиц - их универсальную взаимопревращаемость.

В современной физической литературе, особенно в квантовой механике, квантовой электродинамике и теории элементарных частиц, законам сохранения уделяется огромное внимание. Совместное и раздельное применение известных законов сохранения, отыскание новых инвариантных величин являются прекрасными иллюстрациями действенности ленинской теории познания, стихийного и сознательного применения диалектического метода. Вскрывая внутреннюю противоречивость и единство этих противоречий в мире элементарных частиц и полей, прерывности и непрерывности, "правизны" и "левизны", симметрии и асимметрии, переходов количественных изменений в качественные, открывая новые характеристики материи и движения, физики всего мира идут по пути отыскания более общих законов природы, частными проявлениями которых в конкретных условиях будут известные ныне законы сохранения и другие физические законы. Ядерная физика не заимствует принципы симметрии полностью из классической физики, а пытается открыть новые инвариантные принципы, чтобы отразить новые закономерности и скрытые свойства симметрии, которые существуют, но не проявляются в явлениях обычного макроскопического мира.

Анализ любого эксперимента современной ядерной физики и физики элементарных частиц всегда содержит два основных этапа: применение законов сохранения и других общих законов квантовой теории (общие теоремы о сечениях, принцип детального равновесия и т. п.) и рассмотрение изучаемого явления с точки зрения того или иного предположения относительно характера взаимодействия.

Поскольку законы сохранения связаны с наличием определенной симметрии, становится понятной роль теоретико-группового их осмысления, ибо теория групп изучает наиболее общие следствия, вытекающие из существования того или иного вида симметрии. Законы сохранения с этой точки зрения являются инвариантами соответствующей группы преобразований.

Теоретико-групповой анализ позволяет найти все сохраняющиеся величины для системы движущейся в поле заданной симметрии, обнаружить характер вырождения и возможности его снятия, указать, какие из найденных величин не потеряют свой смысл при изменении симметрии; кроме того, становится возможным разделение характеристик системы на внешние, описывающие ее движения в целом, и внутренние, обусловленные взаимодействием отдельных частей системы. Непосредственное успешное применение теоретико-групповой метод находит, например, в квантовой теории твердого тела, с его помощью могут быть получены результаты важного принципиального значения без необходимости решать уравнения Шредингера.

Теория групп объясняет, почему для получения законов сохранения, отвечающих группе непрерывных преобразований, необходимо и достаточно потребовать инвариантности гамильтониана при бесконечно малом смещении или повороте, откуда будет вытекать инвариантность относительно соответствующего конечного смещения и поворота.

Становится понятным, почему инвариантности гамильтониана относительно пространственной инверсии в классической механике не может соответствовать закон сохранения: классика имеет дело с непрерывными преобразованиями, инверсия же является не собственным преобразованием; в квантовой механике симметрия относительно такого разрывного преобразования приводит к сохранению четности.

У каждого закона сохранения имеется две стороны; в силу их объективного существования они есть прежде всего экспериментальный факт. Их отражение принимает своеобразную форму теоретического осмысления, которое зависит на каждом этапе своего развития от общего уровня знаний и исторически ограниченных представлений и вместе с тем является выражением различия в проявлениях общего закона по отношению к процессам различной природы. Так, существует всеобщий закон сохранения и превращения энергии, отражающий абсолютность, неуничтожимость движения. До его открытия единственной стройной физической теорией была классическая механика. Затем были созданы классическая термодинамика и классическая электродинамика, далее - специальная теория относительности, квантовая механика, релятивистская электродинамика и, наконец, квантовая хромодинамика. Закон сохранения энергии во всех этих теориях является стержневым, но конкретные формы его выражения изменяются, совершенствуются. Несомненно, что дальнейшее развитие теории, а также новые опытные факты приведут к углублению понимания этого фундаментального закона природы.

Но как бы ни углублялся человек в своем познании явлений природы, законы сохранения в уже существующей их форме не теряют своего значения (не говоря уже об их объективном существовании).

Все известные в настоящее время явления и процессы в физике удовлетворительно согласуются с представлением о том, что пространственно-временной континуум непрерывен. Однако есть основание ожидать, что реальное физическое пространство - время имеет не только непрерывную, но и дискретную структуру. Характерно, что В. И. Ленин задолго до получения экспериментальных данных о сложной структуре микромира, развивая материалистическую диалектику, высказал мысль о единстве непрерывного и прерывного в движении, пространстве и времени. "Движение есть единство непрерывности (времени и пространства) и прерывности (времени и пространства). Движение есть противоречие, есть единство противоречий" (2, 29, 231). Вероятно, что в дальнейшем при получении новых экспериментальных данных о структуре элементарных частиц, о внутриядерных силах и других свойствах микромира придется заменить приближенные представления о непрерывном пространстве и времени более точными, учитывающими их дискретность; их симметрия окажется более сложной, и это приведет к изменениям в содержании и составе физических понятий, например, к тому, что выражения для импульса и энергии свободной частицы будут иметь дискретный характер.

Наши знания не только объективны и относительны, но они содержат и частичку абсолютной истины. В законе сохранения и превращения энергии также имеет место соотношение между абсолютным и относительным, и правильно понять его содержание можно только с позиций диалектики абсолютного и относительного в нашем познании.

Абсолютной истиной при характеристике нашего познания является существование в нем объективных истин, т. е. правильного отражения вне нас и независимо от нас существующего материального мира, а также и то, что абсолютное в нашем познании раскрывается через относительное.

Каждая объективная истина в нашем познании имеет абсолютные и относительные моменты в своем содержании, которые не отделены друг от друга, а взаимопроникают друг в друга.

"...Для диалектического материализма,-подчеркивал В. И. Ленин,-не существует непереходимой грани между относительной и абсолютной истиной" (2, 18, 138). Более того, " в (объективной) диалектике относительно (релятивно) и различие между релятивным и абсолютным. Для объективной диалектики в релятивном есть абсолютное. Для субъективизма и софистики релятивное только релятивно и исключает абсолютное" (2, 29, 317).

Опираясь на эти отправные положения диалектического материализма, рассмотрим вопрос о единстве абсолютных и относительных моментов в содержании закона сохранения и превращения энергии. Некоторые ученые, в свое время активно отстаивавшие закон сохранениия и превращения энергии от попыток его "ниспровержения", высказывают в последние годы сомнения в его всеобщности и абсолютности. Причем одно из их утверждений состоит в следующем: "...абсолютен не тот или иной конкретный закон сохранения, а абсолютна идея сохранения" (31. 1962. 5, 75). Это утверждение как раз и свидетельствует о нарушении диалектики абсолютного и относительного. Так как абсолютностью обладает только общая идея сохранения, то конкретные законы сохранения (в том числе и закон сохранениия и превращения энергии) являются относительными и не могут претендовать на какое-либо абсолютное значение.

Отнести абсолютное только к общему, а все содержание конкретного свести к относительному - это и значит разорвать единство абсолютного и относительного, общего и частного. Абсолютное всегда реализуется через относительное как общее через частное. Нет никакого смысла говорить об абсолютности идеи сохранения, не признавая абсолютных моментов в конкретных законах сохранения. Напротив, абсолютность общей идеи сохранения и основывается на том, что в каждом конкретном законе сохранения имеются абсолютные моменты, обобщением которых она и является. Известно, что законы сохранения в физике отличаются друг от друга не только по содержанию, но и по сфере своего действия. Закон сохранения момента импульса не применяется к поступательному движению, закон сохранения барионного заряда не применяется к взаимодействию лептонов и т. д. Сферы действия законов сохранения могут быть более общими и менее общими, но в пределах сферы своего действия каждый закон сохранения в своем содержании имеет абсолютные моменты. Мы, конечно, можем ошибаться в определении сферы действия того или иного закона сохранения, как случилось, например, с законом сохранения четности. Этому закону без достаточных на то оснований сначала приписали более широкую сферу действия, чем та, которую он на самом деле имеет; теперь эта ошибка исправлена, и наши знания об этом законе сейчас имеют более строгий характер, чем ранее.

Сфера действия закона сохранения странности при самом его открытии была определена довольно точно, и поэтому у нас нет оснований ожидать дальнейшего ограничения сферы его действия. Что же касается сферы действия закона сохранения и превращения энергии, то и она к настоящему времени довольно точно определена как физическими, так и философскими исследованиями. Ранее было установлено, что закон сохранения и превращения энергии справедлив для замкнутых, изолированных систем, действует там, где имеют место качественные превращения форм движения материи. При этом давно известно, что всего многообразия этих превращений закон сохранения и превращения энергии не исчерпывает.

Однако давно установлено также и то, что при характеристике этих превращений без сохранения и превращения энергии обойтись нельзя. Поэтому все серьезные попытки доказать возможность ограничения действия закона сохранения и превращения энергии должны быть и доказательствами ограниченности качественных превращений форм движения материи.

Другими словами, чтобы доказать ограниченность закона сохранения и превращения энергии, нужно доказать, что существуют такие области в природе, в которых качественные превращения форм движения материи не происходят. Неотъемлемость, неотделимость закона сохранения и превращения энергии от качественных превращений форм движения материи - это один из важнейших абсолютных моментов в его содержании.

В содержание закона сохранения и превращения энергии далее входит положение о том, что все превращения одних видов энергии в другие происходят всегда и везде в определенных эквивалентных количествах. "...Закон сохранения энергии,-читаем мы в фейнманов-ских лекциях по физике,-не верен, если мы не признаем эквивалентности энергии во всех ее формах..." (149, 188).

Данное положение также является абсолютным моментом в содержании закона сохранения и превращения энергии.

Абсолютным моментом в содержании закона сохранения и превращения энергии, тесно связанным с предыдущим, является широко известное утверждение, что производимая работа происходит за счет источников энергии, что "вечный двигатель" невозможен нигде, никогда и ни при каких условиях.

Это положение в физике часто формулируют так: все законы природы должны быть таковы, чтобы "вечный двигатель" был бы невозможен.

К абсолютным моментам содержания закона сохранения и превращения энергии относятся и его многообразные связи с пространством, временем и причинностью.

На наш взгляд, абсолютными моментами содержания рассматриваемого закона являются и глубокие связи, существующие между энергией и массой, энергией и импульсом, а возможно, и с другими сохраняющимися величинами.

Не все указанные абсолютные моменты в содержании закона сохранения и превращения энергии сразу стали известными, некоторые из них были выявлены лишь в недавнее время, например связь между энергией и массой, связь энергии со временем, выражаемая соотношением ΔE*Δt~h. А это значит, что наши знания об абсолютных моментах содержания данного закона имеют исторический характер, что они непрерывно расширяются и углубляются. Да и вообще знания чего-то абсолютного не являются законченными, завершенными знаниями, истина - это процесс.

В ходе расширения наших знаний о законе сохранения и превращения энергии количество абсолютных моментов в его содержании увеличивается, но никогда мы не сможем сказать, что все абсолютные моменты этого закона нам известны.

Может возникнуть вопрос, почему перечисленные моменты содержания закона сохранения и превращения энергии мы считаем абсолютными. Дело в том, что эти моменты имеют характер неизменных фактов, существование которых подтверждено практикой, и что в процессе развития науки их общее значение все более подтверждается.

Действительно, эквивалентность всех видов энергии и невозможность построения "вечного двигателя" - это непреложный факт, значение которого все более подтверждается. То же самое можно сказать о других абсолютных моментах содержания закона сохранения и превращения энергии. Абсолютное не существует вне относительного и указанные абсолютные моменты закона сохранения и превращения энергии существуют через его относительные моменты и стороны.

Что же является относительным в рассматриваемом законе? Относительными являются, во-первых, формы его проявления в различных областях мира. Каждая из них имеет в принципе ограниченное значение и определенные пределы своей применимости. Например, форма проявления данного закона в механике:

к квантовым процессам, подчиняющимся принципу неопределенности Гейзенберга, не применима, поскольку в этих процессах нельзя одновременно достаточно точно определить кинетическую энергию Т и потенциальную энергию U. Но в ней раскрываются, имеют место в определенных пределах и некоторые абсолютные моменты закона сохранения и превращения энергии. Эта форма закона отчетливо говорит об эквивалентности переходов потенциальной энергии в кинетическую и обратно, а также о невозможности возникновения энергии из "ничего".

Относительное значение имеет и связь закона сохранения и превращения энергии с симметрией трансляции во времени (с однородностью времени). Если его связь со временем вообще абсолютна, то именно с данным свойством времени его связь относительна, и характерна она хотя и для многих, но в принципе не для всех форм проявления данного закона. А это значит, что неоднородность времени автоматически не приведет к нарушению закона сохранения и превращения энергии. Но абсолютная связь этого закона со временем в определенных пределах выражается и через связь некоторых его форм проявления с указанным свойством времени. Относительное значение имеет при формулировке закона сохранения и превращения энергии и понятие об изолированной системе. Относительными сторонами закона сохранения и превращения энергии являются и формы его связи с другими законами сохранения, и формы связи энергии с другими сохраняющимися величинами. Так, не всегда и не везде существует прямая связь между энергией и импульсом, она характерна прежде всего для фотонов, а для электронов, например, только в том случае, когда они движутся с релятивистскими скоростями.

Но в любых ограниченных формах связи закона сохранения и превращения энергии с другими законами сохранения всегда в определенных пределах проявляется ее абсолютный характер. Это значит, что в ходе познания наши знания об этих связях могут измениться, но сам факт их существования остается неизменным и неопровержимым.

Теперь, дав по необходимости очень краткий обзор соотношения абсолютного и относительного в содержании закона сохранения и превращения энергии, поставим вопрос: какой же смысл имеют разговоры о возможностях ограничения этого закона?

Если речь идет о том, что все формы его проявления ограничены, относительны, что наши знания о формах его связи с другими законами сохранения изменчивы и т. д., то все это давно признано.

Но если речь идет об ограничении абсолютных моментов в содержании данного закона, то тому, кто выдвигает это положение, нужно доказывать, что в каких-то условиях существуют неэквивалентные переходы одних видов энергии в другие ее виды, что поэтому возможно возникновение энергии из "ничего" и построение "вечного двигателя", что качественные превращения форм движения материи имеют место не везде, и т. д.

Но доказать все это, оставаясь на почве науки и практики, конечно, невозможно, да и вряд ли кто-нибудь возьмется это доказывать. Поэтому, с нашей точки зрения, все разговоры о возможностях ограничения закона сохранения и превращения энергии просто бесперспективны и ничего науке дать не могут. Было бы более полезным заняться углубленным изучением особенностей различных форм проявления закона сохранения и превращения энергии, его связей с другими законами сохранения, его связей со временем, с процессами отражения и т. д.

Правда, существует путь, не приводящий прямо к таким абсурдам, как допущение возможности возникновения энергии из ничего и т. п., но ведущий к ограничению закона сохранения и превращения энергии. Существо его в том, что признается возможность открытия более общего закона сохранения, чем закон сохранения и превращения энергии. Содержание последнего войдет в этот более общий закон, а энергия станет частным проявлением какой-то более общей сохраняющейся физической величины. В таком случае в каких-то процессах энергия может не сохраняться, как не сохраняется, например, механическая энергия при неупругих ударах, но зато будет сохраняться какая-то более общая физическая величина, что обеспечит невозможность создания "вечного двигателя".

Но возникает вопрос: куда девается энергия в случае ее несохранения? Разумный ответ один - она превращается в какие-то другие физические величины, являющиеся частными проявлениями нашей общей физической величины. Допустив, что энергия есть одно из частных проявлений какой-то более общей физической величины, мы с таким же основанием можем допустить, что другим частным проявлением этой величины является масса, и, таким образом, получаем право говорить о превращении энергии в массу и обратно. Объяснив, далее, частным проявлением этой общей физической величины электрический заряд, мы можем говорить о превращении энергии в электрический заряд и обратно и т.д.

Сделав, на наш взгляд, вполне логичные выводы из этой идеи, мы пришли к давно известному в физике положению об эквивалентности энергии и массы и даже пошли дальше, допустив эквивалентность энергии и электрического заряда. Но так как никаких доказательств превращения энергии в массу и обратно не существует, а есть доказательства взаимосвязи изменений энергии и массы, то вся идея существования физической величины, более общей, чем энергия, и закона сохранения, более общего, чем закон сохранения и превращения энергии, оказывается недостаточно аргументированной. Здесь же нужно отметить, что поиски нового закона сохранения, более общего, чем закон сохранения энергии, и обобщения закона сохранения энергии и других законов сохранения, имеющие место в физике, совсем не одно и то же.

Обобщения закона сохранения и превращения энергии в физике происходят, во-первых, на основе выражения энергии через весьма общие физические функции, например через функции Лагранжа и Гамильтона, во-вторых, на основе (и это более важно) раскрытия связей закона сохранения энергии с другими законами сохранения. Так, физике известны обобщенный закон сохранения энергии-массы, обобщенный закон сохранения энергии-импульса и ряд других.

Эти обобщения отнюдь не ограничивают всеобщность закона сохранения и превращения энергии, а, наоборот, расширяют сферу его применения. В ядерной физике и физике элементарных частиц закон сохранения и превращения энергии применяется именно в своей обобщенной форме как закон сохранения энергии - массы.

Таким образом, попытки ограничения действия закона сохранения и превращения энергии, отрицание его основополагающего значения для современной науки научных оснований под собой не имеют.