§ 4. Скорости галактик больше световой

Согласно закону Хаббла (8) скорость удаления галактик от нас прямо пропорциональна расстоянию и должно существовать некоторое расстояние гъ где скорость удаления становится равной световой, а при еще больших расстояниях скорость должна стать больше скорости света. Правильно ли такое заключение? Нет, неправильно.

Прежде всего, для установления закона Хаббла наблюдаются красные смещения г линий в спектрах галактик, а затем по формуле (7) вычисляются скорости их удаления v. Но мы уже подчеркивали, что формула (7) справедлива только в случае скоростей, малых по сравнению со скоростью света. Если источник света движется со скоростью, близкой к световой (но по-прежнему отсутствуют сильные поля тяготения!), то для вычисления скорости v no z служит более сложная формула специальной теории относительности

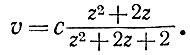
Каково бы ни было z (согласно определению меняться 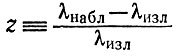оно может меняться в интервале - 1 ≤ z < ∞) скорость v не может превышать с. Если бы какой-нибудь источник, скажем, в нашей Галактике, двигался от нас со скоростью близкой к с, то его скорость надо было бы вычислять по красному смещению спектральных линий z, пользуясь формулой (9). Разумеется, скорость всегда оказывалась бы меньше с.

Но для очень далеких галактик с большим красным смещением z даже эта формула неприменима. Дело в том, что формула (9) не учитывает влияние тяготения на изменение частоты световых волн. Мы увидим далее, что в сильных переменных полях тяготения на больших расстояниях в космологии меняют свой простой привычный смысл понятия расстояния и скорости. Оказывается, сам вопрос: какова скорость по отношению к нам галактики, находящейся очень далеко от нас, - некорректен, неправильно сформулирован. Но об этом позже, а пока вернемся к постоянной Хаббла.