
§ 11. Гравитирует ли вакуум?
Начало истории научной идеи о гравитации пустоты или, на современном научном языке, - вакуума, которую мы изложим в этом параграфе, связано все с тем же конфликтом между традиционной верой в неизменность Вселенной и ее нестационарностью, неумолимо вытекающей из теории тяготения.
Закон всемирного тяготения гласит, что любые материальные тела притягивают друг друга. А гравитирует ли вакуум? Этот вопрос в современной физике был поставлен Альбертом Эйнштейном еще в 1917 г. Что такое гравитация вакуума? Почему возник такой вопрос? Какие данные физических экспериментов или астрономических наблюдений заставили великого физика поставить эту проблему? Оказывается, никаких прямых данных не было, а точнее говоря, именно отсутствие в ту пору данных о движении галактик привело Эйнштейна к мысли о гравитации вакуума.
Дело обстояло следующим образом. Вскоре после создания общей теории относительности Эйнштейн попытался построить на ее основе математическую модель Вселенной. Это происходило до работ Фридмана, до открытия Хабблом красного смещения в спектрах галактик, и Эйнштейном владела идея стационарности, неизменности мира: "Небеса длятся от вечности к вечности". Однако мы видели в § 2, что закон тяготения требует нестационарности Вселенной. Во Вселенной из-за сил тяготения однородно распределенной материи существует отрицательное ускорение, даваемое формулой (10) и нарастающее прямо пропорционально расстоянию.
Для того чтобы уравновесить силы тяготения и сделать мир стационарным, надо ввести силы отталкивания, не зависящие от вещества. Ускорение тяготения и ускорение отталкивания должны быть равны друг другу по абсолютной величине и противоположны по знаку:
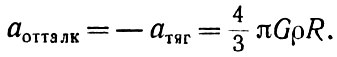
(25)
В первой части равенства мы вместо атяг подставили его значение из (10). Таким образом, сила отталкивания должна быть прямо пропорциональна расстоянию.
Исходя из таких соображений, Эйнштейн ввел космическую силу отталкивания, которая делала мир стационарным. Эта сила универсальна: она зависит не от массы тел, а только от расстояния, их разделяющего. Ускорение, которое эта сила сообщает любым телам, разнесенным на расстояние R, должно быть пропорционально расстоянию и записывается, следовательно, в виде
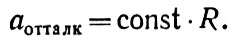
(26)
Зная среднюю плотность вещества во Вселенной (примем ее равной критическому значению ρ = 10-29г/см3), можно по формулам (25) и (26) найти численную величину ускорения и отталкивания:
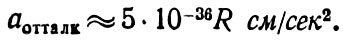
(27)
Численную константу в формуле (27) или, точнее, величину, получающуюся от деления этой константы на квадрат скорости света, называют космологической постоянной и обозначают буквой Л. Итак, согласно идее Эйнштейна
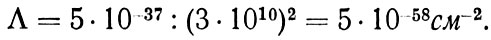
(28)
В принципе силы отталкивания, если они, конечно, существуют в природе, можно было бы обнаружить в достаточно точных лабораторных опытах. Однако малость величины Л делает задачу ее лабораторного обнаружения совершенно безнадежной. Действительно, легко подсчитать, что при свободном падении тела на поверхность Земли добавочное ускорение, сообщаемое силами отталкивания, на 31 порядок (!) меньше самого ускорения свободного падения. Даже в масштабе Солнечной системы или всей нашей Галактики эти силы ничтожно малы по сравнению с силами тяготения. Так, нетрудно подсчитать, что ускорение, сообщаемое Земле тяготением Солнца, равно 0,5 см/сек2. В то же время ускорение космического отталкивания между Землей и Солнцем согласно формуле (27) в 1023 раз меньше! Разумеется, это отталкивание никак не сказывается на движении тел Солнечной системы и может быть обнаружено только при исследовании движений самых отдаленных наблюдаемых галактик.
Так в уравнениях тяготения Эйнштейна появился космологический член, описывающий силы отталкивания вакуума. Действие этих сил столь же универсально, как и сил всемирного тяготения, т. е. оно не зависит от физической природы тела, на котором проявляется, поэтому логично назвать это действие гравитацией вакуума.
Через несколько лет после работы Эйнштейна была создана теория А. А. Фридмана. После того как Эйнштейн признал теорию Фридмана, он стал склоняться к мысли, что Л-член не следует вводить в уравнения тяготения, если их решение для всего мира можно получить и без этого члена.
После открытия красного смещения в спектрах галактик, доказывающего расширение Вселенной, какие-либо основания предполагать, что в природе существуют космические силы отталкивания, отпали. Правда, решение, описывающее расширяющийся мир, можно получить и для уравнений с Λ-членом. Для этого достаточно предположить, что силы тяготения и отталкивания не компенсируют точно друг друга, тогда преобладающая сила приведет к нестационарности. Это было отмечено еще в пионерских работах Фридмана. Наблюдения красного смещения времен Хаббла были недостаточно точны, чтобы определить, какое решение осуществляется в природе: с Λ-членом или без него. Тем не менее многие физики с неприязнью поглядывали на Λ-член в уравнениях, поскольку он осложнял теорию и ничем не был оправдан. Эйнштейн и многие другие физики предпочитали писать уравнения тяготения без Λ-члена, т. е. считая Λ = 0. Эйнштейн назвал введение космологической постоянной в свои уравнения "самой грубой ошибкой в своей жизни".
Однако космологи тридцатых годов не отказались столь поспешно от Λ-члена. Для сохранения Λ-члена у них были серьезные основания. Вспомним, что первые определения постоянной Хаббла давали значения Н ≈ 500 км/сек*Мnс, что соответствовало времени, протекшему с начала расширения Вселенной t ≈ 1/H ≈ 2*1О9 лет (см. § 5, 6). Это очень короткий срок. Во-первых, он оказывался даже меньше возраста Земли. Во-вторых, что гораздо более существенно, возраст звезд и звездных систем тогда ошибочно оценивался в 1013 лет, т. е. на два порядка больше времени расширения Вселенной.
Сегодня мы знаем, что значение t = H-1 было занижено примерно в 10 раз (см. § 5), а возраст звезд, наоборот, завышен более чем на два порядка. И с сегодняшней точки зрения никакого противоречия между этими возрастами нет. Однако в 30-е годы указанное различие рассматривалось как серьезное противоречие.
Для приведения в соответствие времени расширения Вселенной с возрастом звезд был привлечен Λ-член. Так идея универсального космического отталкивания начала переживать период "второй молодости".
Посмотрим, как введение Λ-члена может привести к резкому изменению времени расширения Вселенной*.
* (Заметим, что моделями с Λ-членом много занимался бельгийский ученый Леметр, которому в зарубежной литературе иногда незаслуженно приписывается приоритет создания всей теории расширяющейся Вселенной. Мы уже подчеркивали, что эта теория создана А. А. Фридманом. Говоря о теории расширяющейся Вселенной, Эйнштейн в 1931 г. писал: "Первым на этот путь вступил Фридмгн".)
Предположим, что Λ-член отличен от нуля. Пусть мир расширяется от состояния очень высокой плотности. Так как вначале плотность вещества велика, силы тяготения, пропорциональные плотности и тормозящие расширение, много больше сил отталкивания. Действительно, отношение ускорения, создаваемого тяготением вещества, к ускорению, создаваемому космическими силами отталкивания, есть, согласно формулам (10) и (26)*
* (Напомним, что мы уже не предполагаем справедливости равенства аотталк = - атяг как в модели Эйнштейна. В рассматриваемой модели силы не равны, мир расширяется и плотность ρ падает.)
Когда в начале расширения ρ велико, то это отношение также велико, и силы тяготения много больше сил отталкивания. В ходе расширения рано или поздно плотность упадет настолько, что силы сравняются. В этот момент мир по инерции будет расширяться без ускорения, с постоянной скоростью. Если эта скорость очень мала, то очень долго будет поддерживаться почти полное равенство сил тяготения и отталкивания и, следовательно, период задержки расширения будет длительным. Затем плотность вещества все же постепенно упадет и силы тяготения станут меньше сил отталкивания. Теперь мир уже будет расширяться ускоренно под действием сил отталкивания. График изменения расстояний со временем в такой расширяющейся с задержкой Вселенной изображен на рис. 15. Подбирая параметры модели, можно сделать задержку расширения очень длительной. Согласно этой гипотезе задержка в расширении была в прошлом. Сегодня мир расширяется ускоренно, но значение постоянной Хаббла вовсе уже не определяет времени, прошедшего с начала расширения. Это наглядно видно из рисунка 15.
Так введение Λ растягивает время расширения Вселенной и может привести его в соответствие с возрастом звезд.
Оценки постоянной Хаббла были пересмотрены в 50-х годах. Еще раньше, в конце 30-х годов, было установлено, что превращение водорода в гелий является основным источником энергии звезд, а в 50-х годах построена современная теория звездной эволюции. Все противоречия с возрастами отпали, отпала и необходимость в Λ-члене. Уже во второй раз!
А в 1967 г. начался период "третьей молодости" идеи о Λ-члене. К этому времени астрономы открыли и исследовали необычайные объекты - квазары, о которых мы кратко говорили в § 8.
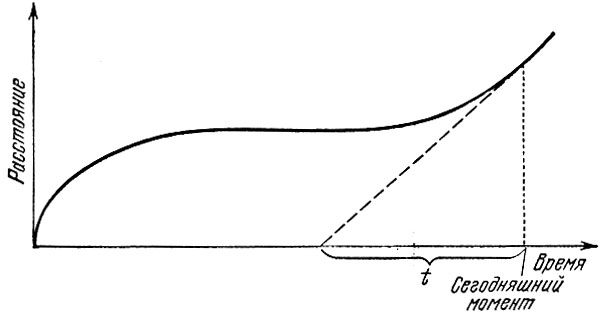
Рис. 15. Изменение с течением времени расстояния между галактиками при Λ ≠ 0. Вначале силы тяготения тормозят расширение, затем, когда силы тяготения сравняются с силами отталкивания, наступает период задержки расширения и, наконец, если силы отталкивания превзойдут силы тяготения, расширение происходит ускоренно. Штриховая прямая показывает, как происходило бы расширение Вселенной с сегодняшней постоянной Хаббла, но без сил тяготения и отталкивания. Время , определенное по постоянной Хаббла, никак не соответствует времени расширения Вселенной
Квазары до сих пор хранят множество тайн и нерешенных проблем. Мы остановимся здесь лишь на двух особенностях квазаров. Как указано в § 5, для галактик давно была известна зависимость между видимой звездной величиной и красным смещением (m ÷z зависимость). Чем дальше галактика, тем она выглядит менее яркой (больше ее звездная величина m), и в то же время тем больше, согласно закону Хаббла, ее скорость, а значит, и красное смещение. Оказалось, что для квазаров такой явной зависимости нет! (см. рис. 16). Американские ученые В. Петросян, Э. Сальпетер и П. Шекере предположили, что отсутствие m ÷ z зависимости у квазаров ч связано с наличием Λ-члена в уравнениях тяготения, т. е. космических сил отталкивания. Поясним сказанное. Американские ученые подчеркивали, что квазары, как правило, наблюдаются на огромных расстояниях, гораздо дальше, чем самые далекие галактики, доступные телескопам. Когда мы наблюдаем квазары с большим красным смещением, т. е. на больших расстояниях, мы видим свет давно испущенный. Если он покинул квазары в эпоху, соответствующую задержке расширения Вселенной в теории с Λ-членом (см. выше), то и у более близкого, и у более далекого квазаров красное смещение будет почти одним и тем же. Это происходит потому, что наблюдения относятся к периоду, когда мир почти не расширялся. Действительно, пусть свет покинул квазар в эпоху задержки расширения. Он долго идет в нерасширяющейся Вселенной и поэтому не краснеет. Когда этот луч находится еще на пути к нам, из более близкого квазара выходит луч, который одновременно с первым в нашу эпоху достигнет наблюдателя на Земле. Теперь оба луча идут вместе по почти стационарной Вселенной и не краснеют. Свет обоих квазаров одинаково покраснеет позже - после окончания эпохи задержки расширения. Следовательно, и относительно близкий, а потому яркий квазар, и далекий, слабый будут обладать почти одинаковым красным смещением. Так Петросян, Сальпетер и Шекере объясняют исчезновение m ÷ z зависимости для далеких квазаров.
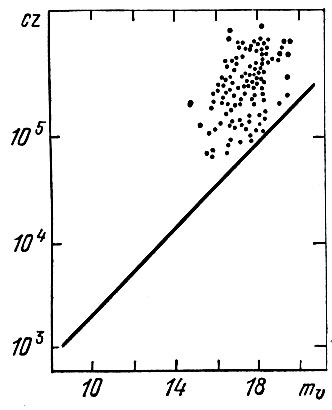
Рис. 16. Зависимость m z для квазаров. Диаграмма красное смещение - видимая звездная величина для квазаров. Прямая линия взята с рис. 5
В пользу картины расширения с задержкой еще более убедительные аргументы привели советские астрофизики И. С. Шкловский и Н. С. Кардашев. У квазаров была обнаружена следующая особенность. Если линии излучения в их спектрах показывают красное смещение, большее 1,95, то линии поглощения, как правило, имеют красное смещение, равное 1,95, И. С Шкловский и Н. С. Кардашев объясняли это тем, что задержка расширения соответствует в прошлом эпохе, от которой мы получаем свет с красным смещением, равным 1,95. Линии излучения возникают в самих квазарах, и поэтому их красное смещение различное. Линии поглощения образуются не в квазарах, а в каких-нибудь галактиках, которые случайно пересекает луч света от квазаров, распространяясь в пространстве. Если период задержки длителен, то наиболее вероятно, что луч квазара пересекает галактику как раз в эпоху задержки расширения и красное смещение линий поглощения будет составлять 1,95. При этом силы отталкивания должны описываться формулой (27) только с численным коэффициентом, в 30 раз большим*. С тех пор прошло 10 лет. Проведено много новых наблюдений квазаров. С одной стороны, выяснилось, что отсутствие четкой зависимости m ÷ z у квазаров связано с сильным разбросом их собственных светимостей (см. § 8). Если выделять однородные группы квазаров с меньшим разбросом светимостей, то зависимость m ÷ z у квазаров внутри такой однородной группы проявляется. С другой стороны, не подтвердились предварительные сообщения о преимущественной концентрации z для линий поглощения квазаров у значения z = 1,95. Снова отпала необходимость в Λ-члене. В третий раз.
* (Увеличение коэффициента в 30 раз обусловлено тем, что почти полное уравновешивание сил тяготения силами отталкивания в гипотезе американских и советских авторов происходит не сегодня, а в прошлом, когда плотность вещества во Вселенной была раз в 30 больше.)
Но, как говорят, джина, выпущенного из бутылки, нелегко загнать обратно. Идея о том, что Λ-член не равен нулю, оказалась живучей.
Ясно одно, что если Λ-член и отличается от нуля, то очень мало. Но доказать, что он точно равен нулю, путем наблюдений, конечно, невозможно. Может быть, действительно существуют космические силы отталкивания?
Это заставляет физиков задуматься над природой таких сил.
Одна из возможных попыток объяснить природу Λ-сил заключается в следующем. Согласно современной квантовой физике, вакуум представляет собой наинизшее энергетическое состояние всех полей. В вакуумe даже в отсутствие реальных частиц происходят сложные процессы рождения и уничтожения так называемых виртуальных частиц. Виртуальные частицы, родившись, не могут разлететься в стороны, став реальными частицами, которые можно зарегистрировать; они тут же аннигилируют друг с другом. Но следствия взаимодействия виртуальных частиц проявляются и с огромной точностью фиксируются экспериментально. Чрезвычайно сложен вопрос о плотности энергии вакуума. Оказывается, во все формулы теории энергия вакуума входит так, что сокращается при описании поведения реальной системы частиц. Возможна и такая формулировка теории, при которой средняя плотность энергии вакуума тождественно равна нулю. Но такой подход годится только до тех пор, пока мы не будем учитывать гравитационное взаимодействие виртуальных частиц.
В период третьего возрождения идеи о Λ-члене (в конце 60-х годов) советский физик Я. Б. Зельдович показал, что возникновение отличной от нуля плотности энергии вакуума наглядно можно представить следующим простейшим образом. В вакууме рождаются и уничтожаются виртуальные частицы с массой m (для простоты мы говорим об одном сорте частиц). Средняя плотность собственной массы (или энергии - величины, отличающейся от плотности массы согласно формуле Эйнштейна Е = mс2 только множителем с2) виртуальных частиц, как сказано выше, в окончательные формулы не входит и может считаться равной нулю. По квантовой теории масса частицы определяет характерное расстояние l = 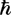 /mc , где
/mc , где 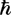 - постоянная Планка, деленная на 2π.
- постоянная Планка, деленная на 2π.
Виртуальные частицы возникают в среднем на характерном расстоянии l друг от друга. Энергия гравитационного взаимодействия соседних частиц, согласно обычной формуле равна*
* (Замечание о знаке этой величины см. в примечании на стр.67.)
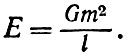
Эта энергия и обуславливает отличную от нуля плотность энергии вакуума или, что то же самое, плотность массы ρвак = εвак/с2. Чтобы получить плотность энергии ε, разделим Е на объем, приходящийся на одну виртуальную частицу, т. е. на l3:
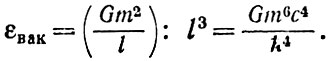
Последнее выражение в формуле получается, если вместо l подставить l = 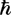 /mс.
/mс.
Но это еще не все. Оказывается, теория требует, чтобы "вакуумная жидкость" обладала давлением, но не обычным давлением, -а отрицательным. Лучше поэтому говорить не о давлении, а о натяжении. По абсолютной величине давление должно равняться плотности энергии и быть противоположным по знаку: ρ = -ε или, используя соотношение Эйнштейна, ρ = -ρс2, ρ/с2 = - ρρ. Это последнее обстоятельство чрезвычайно важно, поскольку именно оно, как мы сейчас увидим, приводит к гравитационному отталкиванию вакуума.
Напомним, что масса однородного шара равна
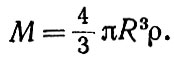
Но согласно теории Эйнштейна эта формула справедлива лишь когда давление вещества пренебрежимо мало по сравнению с величиной ρс2. Если это не так, то
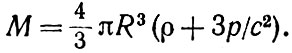
Обычно ρ много больше ρ/с2 и слагаемым Зρ/с2 можно пренебречь. Например, средняя плотность вещества Солнца около 1,4 г/см3, а среднее давление около 2*1015дин/см2. Отсюда (Зρ/с2) : ρ составляет всего 10-6, т. е. весьма малую величину. В то же время для давления и плотности энергии гравитационного взаимодействия вакуумных виртуальных частиц
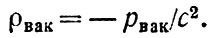
"Вакуумная жидкость", естественно, равномерно заполняет все пространство. Поэтому для вычисления вызываемого ею гравитационного ускорения можно воспользоваться формулой (10), которую мы вывели для равномерно распределенного обычного вещества, с той лишь разницей, что вместо плотности ρ нужно писать cумму
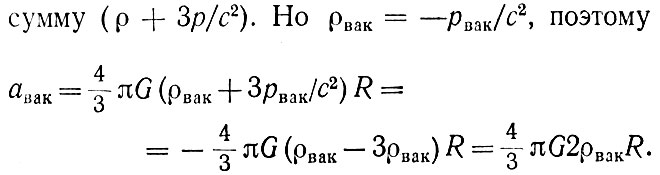
(30)
Таким образом, для гравитации вакуума мы получили не притяжение, как для обычной материи [знак минус в формуле (10)], а отталкивание [знак плюс в окончательном последнем выражении (30)]. Это отталкивание обусловлено, конечно, тем, что давление вакуума отрицательное, и его надо учитывать, согласно теории Эйнштейна, при вычислении гравитационной силы.
Что касается численного значения величины гравитационного отталкивания вакуума, то теория еще слишком груба, чтобы дать сколько-нибудь точное значение. Вернее, теории еще вовсе нет, есть только первые ее наметки, схематически изложенные выше. Можно только очень приближенно вычислить величину отталкивания. Для этого в последнюю формулу надо подставить плотность ρвак = εвак/с2 из выражения для εвак, а затем подставить численные значения констант. Значения констант G, с и h известны с очень большой точностью. Не известна масса m виртуальных частиц (конечно, в действительности надо говорить не об одной частице, а обо всем их спектре), а она входит в формулу в шестой степени, и поэтому величина гравитационного отталкивания чувствительна к ее значению. Если вместо m подставить массу протона, то численный коэффициент в формуле (27) для ускорения отталкивания в 10 млн. раз будет превосходить тот, который по оценкам И. С. Шкловского и Н. С. Кардашева следовал из наблюдений квазаров. Если же взять в качестве m массу электрона, то получится величина, в 100 млрд. раз меньшая, чем приведенная выше. Эта огромная неопределенность отражает несовершенство теоретических представлений. Но уже тот факт, что численные прикидки дают значения, хотя бы отдаленно похожие на те, которые не противоречат астрономическим наблюдениям, указывает, что теория, по-видимому, на верном пути. Кстати, первые попытки вычисления плотности энергии вакуума и его гравитационного действия приводили вообще к величине, в 1046 раз превышающей допустимую из наблюдений, что свидетельствовало о неправильности прежних попыток*.
* (Заметим, что теория в принципе допускает и ситуацию, когда плотность энергии вакуума отрицательна (а не положительна, как мы предположили в тексте) и давление положительно. Тогда в итоге вместо отталкивания получается гравитационное притяжение вакуума. Теория пока еще не может с уверенностью предсказать даже знак эффекта! Вот почему мы не фиксировали внимание в тексте на знаке плотности энергии вакуума. Важно, однако, подчеркнуть, что какой бы знак ни имела плотность энергии вакуума, давление его должно иметь противоположный знак и быть равно плотности по абсолютной величине. Если бы этого не было, то существовала бы выделенная, покоящаяся относительно вакуума система отсчета, в противоречие со специальной теорией относительности.)
Итак, на вопрос "гравитирует ли вакуум?", до сих пор нет окончательного ответа. Если Λ-член и отличен от нуля, то он настолько мал, что не влияет в нашу эпоху сколько-нибудь заметно на процессы в космологии. Еще меньше его влияние было в прошлом, ибо, как мы видели выше, чем более раннюю эпоху рассматривать, чем больше плотность вещества и силы его тяготения, тем меньше роль Λ-члена. По этой причине мы в дальнейшем не будем рассматривать Λ-член.
|
ПОИСК:
|