§ 12. Гравитационный парадокс

В этой главе описана расширяющаяся Вселенная. Неоднократно подчеркивалось, что тяготение требует нестационарности однородно распределенного вещества во Вселенной. Во всех рассуждениях мы пользовались законом тяготения Ньютона. Однако, как уже упоминалось в § 2, применение закона Ньютона для вычисления гравитационного поля, создаваемого всем веществом в бесконечной Вселенной, ведет к противоречию, названному гравитационным парадоксов. Суть этого парадокса заключается в следующем. Пусть Вселенная в среднем равномерно заполнена небесными телами, так что средняя плотность вещества в очень больших объемах пространства одинакова. Попытаемся рассчитать по закону Ньютона, какая гравитационная сила, вызванная всем бесконечным веществом Вселенной, действует на тело (например, галактику), помещенное в произвольную точку пространства. Оказывается, результат расчета неоднозначен, зависит от способа вычисления! Покажем это. Ответ можно получить следующим простым рассуждением. Предположим сначала, что Вселенная пуста. Поместим в произвольную точку пространства пробное тело А. Окружим это тело веществом однородной плотности, заполняющим шар радиуса R, так чтобы тело А было в центре шара. Ясно без всяких расчетов, что в силу симметрии тяготение всех частичек вещества шара в его центре уравновешивает друг друга, и результирующая сила равна нулю, т. е. на тело А не действует никакая сила. Будем теперь добавлять к шару новые и новые сферические слои вещества той же плотности. Мы уже знаем (см. § 2), что сферические слои вещества не создают сил тяготения во внутренней полости и добавление этих слоев ничего не меняет, т. е. по-прежнему равнодействующая сил тяготения для А равна нулю. Продолжая процесс дополнения слоев, мы приходим в пределе к бесконечной Вселенной, равномерно заполненной материей, в которой результирующая гравитационная сила, действующая на А, равна нулю.

Однако рассуждения можно проводить и иначе. Возьмем снова однородный шар радиуса R в пустой Вселенной. Поместим наше тело не в центр этого шара с той же плотностью вещества, что и раньше, а на краю его. Теперь сила тяготения, которая действует на тело А, будет равна, согласно закону Ньютона

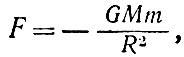
(31)

где М - масса шара, m - масса пробного тела А. Будем теперь добавлять cферические слои вещества к шару. После того как к этому шару добавлена сферическая оболочка, она не добавит гравитационных сил внутри себя. Следовательно, сила тяготения, действующая на тело A, не изменится и по-прежнему равна F [формула (31)].

Продолжим процесс добавления сферических оболочек вещества одинаковой плотности. Сила F остается неизменной. В пределе мы снова получаем Вселенную, заполненную однородным веществом с той же плотностью. Однако теперь на тело А действует сила F. Очевидно, в зависимости от выбора первоначального шара, можно получить произвольную силу F после перехода к однородно заполненной веществом Вселенной. Вот эта неоднозначность и получила название гравитационного парадокса.

Итак, теория Ньютона не дает возможности без добавочных предположений однозначно рассчитать гравитационные силы в бесконечной Вселенной. Только теория Эйнштейна позволяет рассчитать эти силы без всяких противоречий. В конце параграфа мы вернемся к этому вопросу и обсудим, почему мы все же могли использовать теорию Ньютона для наших выводов в § 2 и других.

А сейчас посмотрим, почему в космологии мы обязаны перейти от теории Ньютона к теории Эйнштейна при изучении огромных масштабов космоса.

В связи с этим разберем, почему вообще возникает необходимость обобщения закона Ньютона.

Теория Ньютона предполагает мгновенное распространение тяготения и уже поэтому не может быть согласована со специальной теорией относительности, утверждающей, что никакое взаимодействие не может распространяться со скоростью, превышающей скорость света в вакууме.

Нетрудно найти условия, ограничивающие применимость теории тяготения Ньютона. Так как эта теория не согласуется со специальной теорией относительности, то ее нельзя применять всякий раз, когда гравитационные поля настолько сильны, что разгоняют движущиеся в них тела до скорости, близкой к скорости света в вакууме с. Скорость, до которой разгоняется тело, свободно падающее из бесконечности (где оно имело пренебрежимо малую скорость) до некоторой точки, равна по порядку величины корню квадратному из модуля гравитационного потенциала φ в этой точке (на бесконечности φ считается равным нулю). Таким образом, теорию Ньютона можно применять только в том случае, если

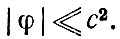
(32)

Кроме того, эта теория не применима и к расчету движения частиц даже в слабом поле тяготения, удовлетворяющем условию (32), если частицы уже вдали от тяготеющих масс имели скорость, близкую к с. В частности, теория Ньютона не применима для расчета траектории света в поле тяготения. Хотя теория Ньютона и предсказывает искривление луча света в поле тяготения, но численно дает результат, отличающийся от результата релятивистской теории тяготения. А именно результат последней теории подтверждается наблюдениями. Наконец, теория Ньютона не применима при расчетах переменного поля тяготения, создаваемого движущимися телами (например, двойными звездами) на расстояниях r, больших, чем λ = cτ, где τ - характерное время движения в системе (например, период обращения в системе двойной звезды). Действительно, в этом случае, согласно ньютоновской теории, поле тяготения на расстояниях r "мгновенно подстраивается под положение тел в данный момент, но согласно специальной теории относительности изменение поля, происходящее за характерное время τ, не может распространяться до r со скоростью, превышающей скорость света.

Обобщение теории тяготения на основе специальной теории относительности было сделано А. Эйнштейном в 1916 году. С некоторыми выводами теории мы познакомимся в следующей главе.

Вернемся теперь к космологии. Покажем, что в космологии мы встречаемся с такой ситуацией, когда поля тяготения настолько сильны, что должны разгонять падающие в них тела до световых скоростей.

Рассмотрим снова однородный шар произвольного радиуса R с плотностью вещества ρ, находящийся в пустоте. Если мы будем увеличивать размер рассматриваемого шара, не меняя плотности вещества, то, очевидно, масса шара возрастает пропорционально кубу радиуса. В то же время гравитационная сила на поверхности шара обратно пропорциональна квадрату радиуса. Произведение обоих факторов дает в результате увеличение силы тяжести пропорционально первой степени радиуса. Значит, переходя от шара к бесконечной Вселенной, мы рано или поздно получим гравитационное поле на поверхности шара настолько большим, что теория Ньютона становится неприменимой.

Можно привести и немного более подробные рассуждения и получить оценку расстояния в нашей реальной Вселенной, на котором уже неприменима теория Ньютона.

Скорость, которую приобретает любое тело, свободно падающее из состояния покоя с большого расстояния на поверхность гравитирующего шара, совпадает, очевидно, со скоростью, которую должно иметь тело, чтобы улететь с поверхности шара в бесконечность, т. е. совпадает со второй космической скоростью.

Выпишем еще раз формулу для нее:

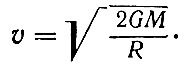
(33)

Скорость падения, равная скорости света, достигается, следовательно, если масса шара достаточно велика по сравнению с радиусом. А именно из (33), подставляя вместо v скорость света с, находим, что критический радиус шара массы М должен равняться

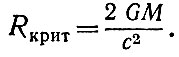
(34)

Этот радиус в общей теории относительности носит название гравитационного радиуса.

Теперь, подставляя в (34) вместо М выражение массы через плотность и объем 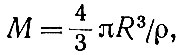, находим

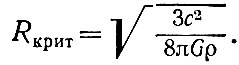
(35)

Для получения численного значения R_крит надо подставить в эту формулу ρ.

Средняя плотность вещества во Вселенной ρ известна из наблюдений, хотя и не точно (см. § 9). Для оценки можно принять ρ = 10^-30г/_см³. Теперь все величины в правой части выражения (35) известны, и мы находим критическое расстояние

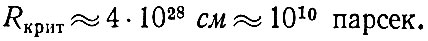
(36)

Итак, когда в астрономии рассматриваются расстояния больше чем примерно десять миллиардов парсек, то необходимо уже пользоваться общей теорией относительности.

Внимательный читатель, конечно, спросит: почему же, когда мы переходим к меньшим расстояниям, мы все же можем пользоваться ньютоновской теорией? Ведь, как было показано в начале параграфа, ньютоновская теория приводит к гравитационному парадоксу, к неоднозначности вычисления силы тяготения во Вселенной и, следовательно, этой теории нельзя доверять ни в каких масштабах. Строго говоря, читатель прав. Теория тяготения Ньютона сама по себе не позволила бы убедительно получить правильный результат ни для какого масштаба. Однако если читатель вернется к § 2, где обосновывалась возможность использовать для малых масштабов во Вселенной теорию Ньютона, то заметит следующее. Утверждается, что если взять релятивистскую теорию тяготения Эйнштейна (которая кратко описывается в следующей главе и которая применима ко Вселенной без всяких парадоксов), то согласно этой теории сферически-симметричное распределение материи (конечное или бесконечное - неважно) не создает никакого гравитационного поля внутри сферической полости (рис. 17). Это утверждение теории Эйнштейна строго и получается, в отличие от теории Ньютона, однозначно.

Рис. 17. Бесконечное сферически-симметричное распределение вещества не создает никакого гравитационного поля внутри сферической полости

После этого можно рассматривать шар, как раз заполняющий полость, с плотностью вещества равной плотности внешнего вещества. Для этого шара, если он достаточно мал и его поле тяготения не велико, можно применять теорию Ньютона. Такой путь законен и строг, и мы так поступали, избегая гравитационного парадокса.

К сказанному надо добавить, что в космологии в принципе измеримыми величинами являются относительные скорости галактик и относительные ускорения их. Величина силы тяготения F становится определенной только, если мы выбрали центр шара, или, как говорят в теории относительности, выбрали систему отсчета. Но выбор центра шара, выбор системы отсчета произволен! Вот почему величина силы F становится относительной, впрочем, как и другие понятия ньютоновской теории, когда мы переходим к релятивистской теории, включая понятия пространственной протяженности и временной длительности.

Подытожим сказанное. В сравнительно малых участках пространства, меньше примерно десяти миллиардов парсек, можно пользоваться ньютоновской теорией для решения космологических задач. В частности, эта теория помогает понять, почему Вселенная нестационарна. В масштабах, сравнимых с критическим и больше, и тем более для анализа структуры Вселенной в целом, необходима релятивистская теория тяготения. А. Эйнштейн писал: "С моей точки зрения, без использования принципов общей теории относительности невозможна достичь теоретическим путем каких-либо, хоть в какой-то мере надежных, результатов в области космологии".

В следующей главе мы рассмотрим кратко релятивистскую теорию тяготения и релятивистскую космологию.