Глава 2. Релятивистская космология

§ 1. Основная идея теории тяготения Эйнштейна

Мы начнем эту главу с краткого описания основных идей и выводов общей теории относительности Эйнштейна (релятивистской теории тяготения), которую советские физики Л. Д. Ландау и Е. М. Лифшиц назвали "самой красивой из всех существующих физических теорий". Разумеется, здесь теория не будет излагаться сколько-нибудь подробно. Не касаясь в деталях математического аппарата теории, мы приведем только самые необходимые сведения, нужные для понимания проблем современной космологии^*.

^* (Об обосновании теории тяготения Эйнштейна см. § 5 гл. 5.)

Самой важной особенностью поля тяготения, обнаруженной Галилеем и Ньютоном и положенной Эйнштейном в основу его теории, является то, что оно совершенно одинаково действует на различные тела, сообщая им одинаковые ускорения независимо от их массы, химического состава и других свойств. Этот факт был установлен опытным путем еще Галилеем, и может быть сформулирован как принцип строгого равенства весомой массы тв (определяющей взаимодействие тела с полем тяготения и входящей в закон всемирного тяготения; см. (31) гл. 1) и инертной массы m_и (определяющей сопротивление тела действующей силе и входящей во второй закон механики Ньютона). Действительно, запишем, например, уравнение движения (второй закон механики Ньютона) для тела, находящегося в поле тяготения шара массы М_в:

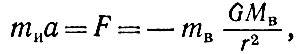
(1)

где а - ускорение, приобретаемое телом под действием гравитационного поля. Если m_и равно m_в, то они сокращаются в уравнении (1), и ускорение а не зависит от массы движущегося тела и определяется только напряженностью поля тяготения (так называют величину 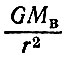) в согласии с законом Галилея. Современные опыты в лаборатории подтверждают закон Галилея с огромной точностью. Так, советский физик В. Б. Брагинский показал, что m_и и m_в равны с точностью не хуже 10^-12!

Со школьной скамьи мы привыкли к тому, что масса во втором законе механики m_и и масса тв в уравнении тяготения - это одно и то же. Но это не более чем привычка! Действительно, если бы мы рассматривали движение тела не в поле тяготения, а скажем, движение электрически заряженного тела в поле другого заряда, то слева в уравнении (1) по-прежнему стояла бы масса тт а справа вместо масс стояли бы электрические заряды. Именно они определяют силу. Таким образом, тв это скорее гравитационный заряд! И то, что он оказывается равным m_и, является удивительным фактом, требующим разгадки^*.

^* (Точнее, надо говорить о пропорциональности m_и и m_в, а не о равенстве. Действительно, если бы m_в и m_и были не равны, а пропорциональны в (1), то ускорение свободного падения все равно бы не зависело от массы. Равенство ти и т3 тогда достигается специальным выбором единиц измерения для m_и и m_в. Но это уже несущественные тонкости.)

Таким образом, тела разной массы, разной природы движутся в заданном поле тяготения совершенно одинаково, если только их начальные скорости были заданы одинаковыми. Этот факт показывает глубокую аналогию между движением тел в поле тяготения и движением тел в отсутствии тяготения, но при наблюдении их из ускоренной системы. Так в отсутствии тяготения тела равной массы движутся по инерции прямолинейно и равномерно. Если наблюдать эти тела из кабины космического корабля, который движется с постоянным ускорением за счет работы двигателя, то, естественно, по отношению к кабине все тела будут двигаться с постоянным ускорением, противоположным ускорению корабля. Движение тел будет таким же, как падение с одинаковым ускорением в постоянном поле тяготения. Следовательно, ускоренная система отсчета (связанная с космическим кораблем) эквивалентна гравитационному полю. Этот факт выражает принцип эквивалентности Эйнштейна. Согласно этому принципу можно осуществить и процедуру, обратную описанной выше имитации поля тяготения ускоренной системой, а именно, можно "уничтожить" в данной точке истинное гравитационное поле введением системы отсчета, движущейся с ускорением свободного падения. Действительно, хорошо известно, что в кабине космического корабля, свободно без двигателей движущегося вокруг Земли в ее поле тяготения, наступает состояние невесомости - не проявляются силы тяготения. Эйнштейн предположил, что не только механическое движение, но и вообще все физические процессы в истинном поле тяготения, с одной стороны, и в ускоренной системе в отсутствие тяготения, с другой стороны, протекают по одинаковым законам. Этот принцип получил название "сильного принципа эквивалентности", в отличие от "слабого принципа эквивалентности", касающегося только закона движения тел в пространстве.

Рассмотренная выше система отсчета (космический корабль с работающим двигателем), движущаяся с постоянным ускорением в отсутствии поля тяготения, имитирует только однородное гравитационное поле, одинаковое по величине и направлению во всем пространстве. Поля тяготения, создаваемые отдельными телами, не таковы. Для того чтобы имитировать сферическое поле тяготения Земли, например, нужны ускоренные системы с различным направлением ускорения в различных точках. Наблюдатели в разных системах, установив между собой связь, обнаружат, что они движутся ускоренно друг относительно друга, и тем самым установят отсутствие истинного поля тяготения. Таким образом, истинное поле тяготения не эквивалентно просто ускоренной системе отсчета в обычном пространстве, или, говоря точнее, в пространстве - времени специальной теории относительности. Однако Эйнштейн показал, что если, исходя из принципа эквивалентности, потребовать, чтобы истинное гравитационное поле было эквивалентно в каждой точке локальным ускоренным системам отсчета, то глобально пространство - время окажется искривленным - неевклидовым. Это означает, что в трехмерном пространстве геометрия окажется неевклидовой - сумма углов треугольника не равна π, отношение длины окружности к радиусу не равно 2π и т. д., а время в разных точках будет течь по-разному. Таким образом, согласно теории тяготения Эйнштейна истинное гравитационное поле является ничем иным, как проявлением искривления (отличия геометрии от евклидовой) четырехмерного пространства - времени. Мы говорим именно о четырехмерном пространстве - времени, ибо уже специальная теория относительности (не рассматривающая тяготение) установила связь между пространством и временем. Эта теория описана во многих популярных книгах, и мы здесь на ней не останавливаемся.

Следует подчеркнуть, что создание теории тяготения Эйнштейна стало возможным только после открытия неевклидовой геометрии трудами Лобачевского, Больяи, Римана, Гаусса и др.

В отсутствие тяготения в пространстве-времени специальной теории относительности движение тела по инерции изображается прямой линией или, как говорят математики, экстремальной (геодезической) линией. В плоском пространстве экстремальная линия есть прямая.

Идея Эйнштейна, основанная на принципе эквивалентности и составляющая основу теории тяготения, заключается в том, что и в поле тяготения все тела движутся по экстремальным (геодезическим) линиям в пространстве-времени, которое, однако, уже искривленное, и следовательно, геодезические линии уже не прямые. Конечно, искривление пространства, а тем более искривление 4-х мерного пространства-времени невозможно представить себе наглядно. Но физики уже давно привыкли иметь дело с совершенно не наглядными понятиями (вспомним квантовую механику, например). Искривленность (или неевклидовость) означает, что геометрия многообразия определяется аксиомами, отличными от евклидовых. Свойства экстремальных линий в таких пространствах отличаются от свойств прямых. Примером экстремалей на двумерной кривой поверхности могут служить дуги больших кругов на поверхности шара.

Массы, создающие поле тяготения, искривляют пространство-время. Тела, которые движутся в этом искривленном пространстве-времени, и в этом случае движутся по одним и тем же геодезическим линиям, независимо от массы или состава тела. Наблюдатель воспринимает это движение как движение по искривленным траекториям в трехмерном пространстве с переменной скоростью. Но с самого начала в теории Эйнштейна заложено, что искривление траекторий, закон изменения скорости - это свойства пространства-времени, свойства геодезических в этом пространстве-времени, а значит, ускорение любых тел должно быть одинаково, значит, весомая масса m_в должна равняться инертной m_и так, чтобы ускорение в (1) было одинаково для всех тел.

Таким образом, поле тяготения есть отклонение свойств пространства-времени от свойств плоского многообразия. Уравнения тяготения Эйнштейна связывают величины, описывающие искривленность пространства- времени (т. е. величину поля тяготения) с величинами, создающими это искривление (т. е. создающими поле тяготения). Согласно теории Эйнштейна в эти величины, создающие поле тяготения, входят не только массы (как было у Ньютона), но и кинетическая энергия движения вещества, давление, а в более сложных случаях и другие характеристики физической материи. Все виды физической материи испытывают действие поля тяготения (это ведь искривленность пространства-времени), и все виды материи участвуют в создании этого поля. Так, поле тяготения зависит, например, и от электромагнитных полей и от других физических полей.

Как уже говорилось, мы здесь не будем выписывать сами уравнения Эйнштейна в общем виде. Все равно без изучения сложного математического аппарата общей теории относительности мы не смогли бы описать, как их решать и использовать. Сказанного о теории Эйнштейна достаточно для понимания дальнейшего. По мере необходимости мы будем приводить отдельные выводы из уравнений этой теории.

Конечно, в случае слабых полей уравнения Эйнштейна переходят в закон всемирного тяготения Ньютона, а пространство-время мало отличается от плоского (евклидова) пространства-времени.