
§ 2. Геометрические свойства пространства Вселенной
Обратимся теперь к космологии и будем рассматривать области пространства, сравнимые с Rкрит и большие, чем Rкрит (определенный в § 12 гл. 1), при исследовании которых надо использовать релятивистскую теорию.
Мы будем рассматривать большие области пространства, в которых распределение материи можно считать однородным (см. гл. 1) и все свойства не зависят от направления. Как уже было сказано во введении к книге, космологическая модель при таких предположениях была построена А. А. Фридманом на основе теории Эйнштейна.
Нас сейчас будет интересовать главным образом искривление, геометрия трехмерного пространства, но всегда надо помнмъ, что в общей теории относительности искривлено, не только трехмерное пространство, но и четырехмерное пространство-время.
Еще раз напомним, что все эти усложнения по сравнению с классическими представлениями механики Ньютона необходимы. В механике Ньютона было абсолютное пространство и в нем двигались тела. Специальная теория относительности показала, что абсолютного пространства нет, нет абсолютного движения и для определения движения надо вводить систему отсчета. Только после указания системы отсчета имеет смысл говорить, как по отношению к ней движутся тела. Общая теория относительности показала, что пространство-время искривлено в зависимости от тяготения вещества (точнее, искривление и есть проявление тяготения). Если тяготеющее вещество движется, то искривление меняется со временем. Значит, любая система отсчета будет изменяться, деформироваться. Таким образом, нет жесткого каркаса-сетки неизменных пространственных координат, все они в переменных гравитационных полях обязаны деформироваться*.
* (Разумеется, в слабых полях все деформации в сетке координат, связанные с изменением кривизны пространства - времени, могут быть сделаны пренебрежимо малыми. Иное дело в космологии, когда мы охватываем большие массы вещества; здесь изменения искривления пространства - времени велики и жесткая сетка координат неприменима. Вот почему мы говорили в §4, что теряет однозначный смысл утверждение о скорости удаления очень далеких галактик. Ведь к ним не протянуть мысленно, даже в принципе, жестких масштабных стержней, по отношению к которым определяется скорость. Специальная теория относительности установила, что нет абсолютного пространства, нет абсолютной скорости. Но согласно этой теории, после того как выбрано состояние движения наблюдателя, с ним можно связать мысленно жесткую сетку координат и по отношению к ней измерять скорость тел на любом расстоянии от наблюдателя. Общая теория относительности утверждает, что в полях тяготения и после выбора наблюдателя абсолютно жесткой протяженной сетки координат с ним не свяжешь, поэтому и нет однозначного определения скорости далеких галактик (для таких расстояний неизбежные деформации сетки особенно велики). Но отсутствие однозначного определения скорости удаления галактик не мешает теории Эйнштейна точно и однозначно вычислять красное смещение спектральных линий далеких объектов, видимую яркость объектов и другие наблюдаемые величины.)
После этих необходимых кратких разъяснений вернемся к космологии. В однородной изотропной космологической модели Фридмана выбор системы отсчета естествен. Выберем систему отсчета как координатный каркас, расширяющийся вместе с системой галактик (точнее, скоплений галактик). Галактики по отношению к этому каркасу покоятся*. Такая система отсчета получила название сопутствующей. Мы будем ею пользоваться и изучать геометрические свойства "сопутствующего", как говорят, пространства этой системы отсчета.
* (Галактики, помимо общей скорости расширения, имеют еще сравнительно небольшие случайные скорости. Эти скорости составляют обычно сотни (иногда тысячи) км/сек. Мы не рассматриваем здесь случайные скорости галактик, усредняем их движение.)
Что такое искривление пространства? Это изменение его геометрических свойств. Мы наглядно можем пред-ставить себе искривленную двумерную поверхность (например, поверхность шара, или поверхность гиперболоида; рис. 18). На таких поверхностях геометрия отличается от геометрии на плоскости. Однако эта аналогия вряд ли поможет нам представить наглядно искривленное трехмерное пространство. Мы живем в трехмерном пространстве, выпрыгнуть из него не можем (так как вне пространства ничего нет), поэтому нельзя спрашивать: "в чем изгибается наше реальное пространство?*. Суть кривизны пространства заключается в изменении его геометрических свойств по сравнению со свойствами плоского пространства, где справедлива геометрия Евклида.
* (Хотя, конечно, в математике рассматривается "вложение" искривленного трехмерного пространства в воображаемые пространства большего числа измерений.)
В искривленном пространстве аналогом плоскостей являются геодезические поверхности, аналогом прямых- геодезические линии. Как уже говорилось, треугольник из геодезических линий имеет в искривленном пространстве сумму углов, отличную от я (или, что то же, от 180°) и зависящую от площади, длина окружности не равна 2πr и т. д. Кривизна двумерной поверхности в данной точке характеризуется одним числом. Это число определяется следующим образом. Измеряется сумма углов деляется следующим ооразом. измеряв маленького треугольника, начерченного вокруг данной точки. На кривой поверхности она либо больше, либо меньше, чем π. Можно доказать, что разность суммы углов ∑ и π пропорциональна площади треугольника S:
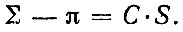
(2)
Коэффициент пропорциональности С называют кривизной. Величина С может быть и положительна и отрицательна. Корень квадратный из величины 1/С называют радиусом кривизны. Если С отрицательно, то радиус кривизны мнимый. Например, на поверхности шара (во всех точках кривизна, естественно, одинакова) - положительна, и равна квадрату радиуса шара; радиус кривизны есть радиус шара. Примером поверхности отрицательной кривизны является поверхность однополостного гиперболоида на рис. 18.
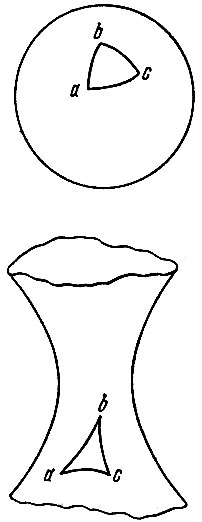
Рис. 18. Двумерные искривленные поверхности. Вверху: сфера - поверхность с положительной кривизной. Сумма углов треугольника на сфере больше π. Внизу: однополостный гиперболоид - поверхность с отрицательной кривизной. Сумма углов треугольника на гиперболоиде меньше π
Кривизна трехмерного пространства - понятие более сложное. Но нас интересует сейчас простой случай однородной изотропной Вселенной. Здесь кривизна пространства характеризуется также одним числом - кривизной, которое определяется как и для поверхности. Уравнения общей теории относительности показывают, что если плотность материи во Вселенной меньше критического значения (см. гл. 1) ρкрит = 10-29г/см3, то кривизна пространства отрицательна, если же больше этого значения, то кривизна положительна.
Величина кривизны и ее знак в однородной Вселенной одинаковы во всех точках пространства в один и тот же момент времени. Величина радиуса кривизны зависит от постоянной Хаббла H и плотности вещества и выражается формулой
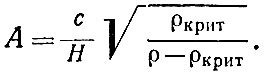
(3)
Здесь с - скорость света. Так, для плотности ρ, в два раза превышающей критическое значение, получаем радиус кривизны
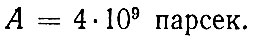
(4)
Если плотность вещества меньше критической, то радиус кривизны мнимый, а сама кривизна (являющаяся квадратом радиуса кривизны) - отрицательна. В этом случае характеристикой искривленности является абсолютная величина мнимого радиуса.
Плотность вещества и постоянная Хаббла меняются с течением времени, меняется и радиус кривизны, но знак кривизны неизменен в течение всей эволюции. Радиус кривизны меняется со временем точно так же, как и расстояние между любой парой галактик. Поэтому график рис. 9 является одновременно и графиком для изменения с течением времени величины А. Для случая ρ < ρкрит величина А равна нулю в начале расширения и затем неограниченно возрастает. Для случая ρ > ρкрит величина А растет, достигает максимума и снова уменьшается до нуля.
|
ПОИСК:
|