§ 3. Замкнутый и открытый мир

Посмотрим, к каким конкретным выводам ведет искривленность пространства. Если кривизна пространства Вселенной отрицательна (т. е. если действительная плотность вещества меньше критической ρ < ρ_крит) или равна нулю, то пространство бесконечно простирается во все стороны, содержит бесконечное количество небесных тел, элементарных частиц и галактик. Такой мир носит название открытого мира. Качественно структура этого мира такая же, как и привычного евклидова мира.

Однако, если ρ > ρ_крит, кривизна положительна, а трехмерное пространство оказывается замкнутым и конечным (но безграничным). Снова приходится повторять, что все наши наглядные представления основаны на повседневном опыте и относятся к евклидову трехмерному пространству. Поэтому наглядно представить себе замкнутую Вселенную невозможно: можно лишь изучать математически ее свойства, сравнивать результаты расчетов с опытом и наблюдениями и пояснять их с помощью аналогий и моделей, но, как всегда, любые модели и аналогии являются неполными. Итак, каковы свойства замкнутой Вселенной? Возьмем какую-либо точку (например, нашу Галактику) в качестве начала координат. Построим вокруг нее сферу, т. е. рассмотрим совокупность галактик, равноудаленных от той, которая находится в начале координат. На сфере можно измерить длину экватора сферы и площадь поверхности сферы. При этом нужно иметь в виду нестационарность модели Вселенной. Вселенная расширяется и сфера, проходящая через одни и те же галактики, изменяет свой размер. Длина экватора и площадь-сферы, ограничивающей данную совокупность галактик, зависят от того, в какой момент мы их измерим. Для того чтобы измерения проводились для всех сфер в один момент времени, введем понятие собственного времени. Это время отсчитываем от момента бесконечной плотности по часам, которые движутся вместе с частицей. Здесь мы рассматриваем только движение частиц, соответствующее всеобщему расширению, т. е. не учитываем отклонения скорости отдельных галактик от той скорости, которая в данной точке должна быть в однородной расширяющейся Вселенной. Условимся все величины измерять в тот момент, когда собственное времся частиц одинаково, т. е. в один момент для всех галактик.

Оказывается, что при ρ > ρ_крит, т. е. в случае замкнутого мира, по мере перехода ко все более удаленным сферам в один и тот же момент времени длина экватора и площадь сферы вначале возрастают, как и в обычном плоском пространстве, но потом проходят максимум, и затем уменьшаются до нуля.

Таким образом, на достаточно больших расстояниях сфера, более удаленная от начала координат, охватывающая больше вещества и имеющая больший объем, в то же время имеет меньший экватор и меньшую поверхность. Это непривычно, не похоже на евклидову геометрию, но является следствием кривизны пространства. Чтобы сделать сказанное более понятным, обратимся снова к аналогам с искривленными двумерными поверхностями. Аналогией замкнутого трехмерного пространства является замкнутое кривое двумерное пространство - поверхность обычного трехмерного шара. Возьмем северный полюс за начало координат. Аналогами сфер на поверхности шара являются окружности вокруг полюса, т. е. параллели. Длина окружности вначале растет по мере удаления от северного полюса, но затем на экваторе достигается максимум и далее длина окружности уменьшается, между тем площадь, охваченная окружностью, монотонно растет. При приближении окружности к южному полюсу площадь, охваченная окружностью, монотонно растет. Наконец, при приближении окружности к южному полюсу площадь, охваченная ею, становится равной 4πr², а длина стремится к нулю.

Заметим, что параллель разделяет всю поверхность на две части, каждая из которых конечна. Площадью поверхности, ограниченной параллелью, мы всегда называем поверхность части сферы, лежащую севернее параллели и включающей в себя северный полюс. При таком определении стягивание параллели к южному полюсу сопровождается стремлением к 4πr² площади поверхности, ограниченной этой параллелью.

Мы видим, что двумерное пространство постоянной положительной кривизны оказалось конечным по площади, замкнутым само на себя и не имеющим никакой границы. Муха, ползущая по сфере, не встретит никогда ни края, ни преграды. Кратчайшая линия - геодезическая, вышедшая из северного полюса, обогнув всю сферу, вернется в исходную точку к северному полюсу.

Вернемся к трехмерному замкнутому пространству, которым является однородная Вселенная в том случае, если ρ > ρ_крит. Здесь мы также называем внутренностью сферы вокруг начала координат, ту часть пространства, которая содержит начало координат. Как мы видели выше, с удалением от выбранного начала охватывающие его сферы сначала увеличиваются в размерах, а затем уменьшаются, стягиваясь в точку. Это как раз и означает, что рассматриваемое трехмерное пространство является замкнутым. В замкнутой однородной Вселенной геодезическая линия, выходящая из начала координат, подобно дуге большого круга на сфере, вышедшей из северного полюса, огибает конечный мир и возвращается в начало координат, т. е. "прямые" линии (геодезические) оказываются замкнутыми. Полная длина такой замкнутой линии выражается через радиус кривизны пространства А и равна 2πA.

Надо еще раз подчеркнуть, что замкнутый мир тем не менее безграничен. Нет никакой границы в мире, за которую нельзя бы было двигаться. Вне этого замкнутого пространства ничего нет. Объем замкнутого мира конечен. Мир содержит конечное число небесных тел, галактик, частиц. Объем замкнутого мира выражается через его радиус кривизны А:

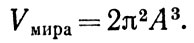
(5)

Величина радиуса кривизны определяется через ρ и Н по формуле (3). Напомним, что А изменяется со временем, следовательно, меняется и объем V мира. Объем равен нулю в начале расширения, затем с течением времени увеличивается, достигает максимума в момент максимума А и вновь сжимается к нулю. Таким образом, принципиальная важность определения того, больше ли плотность критической или меньше, связана не только с тем, что от этого зависит будущая эволюция Вселенной во времени, но и с тем, что это определяет протяженность Вселенной в пространстве.

В заключение сделаем еще одно замечание. Изучая случай замкнутой Вселенной, мы рассмотрели модель, которая необходимо приводит к пространству с топологическими свойствами, резко отличающимися от топологии обычного евклидова пространства. Но надо подчеркнуть, что топологические свойства пространства (т. е. общие свойства пространства в целом) не определяются только его кривизной, только его внутренней геометрией. Для примера опять обратимся к двумерной аналогии. Возьмем плоскость с геометрией Евклида. Как бы мы ни изгибали плоскость (но не делали на ней складки и не разрывали!), свойства фигур на ней не изменятся, т. е. геометрия будет оставаться евклидовой - сумма углов треугольника равна я, кривизна С = 0. Вырежем теперь из плоскости бесконечную полоску и свернем ее в бесконечно длинный цилиндр (рис. 19). И у плоскости и у цилиндра кривизна С = 0, обе поверхности не имеют границ (муха и по цилиндру может ползти, не встречая края). Но топологические свойства у них совершенно разные! Так, на цилиндре некоторые геодезические замкнуты (см. рис. 19), другие бесконечны и т. д. Возможны и другие более сложные топологические построения. Таким образом, этот простейший пример с ЛВУ мерной поверхностью показывает, что кривизна еше не определяет однозначно всех свойств поверхности Топология задается дополнительно. То же самое справедливо и в отношении трехмерного пространства (и пространств большего числа измерений). Общая теория относительности определяет только геометрию пространства (точнее, четырехмерного пространства - времени) и ничего не говорит в общем случае о его топологии.

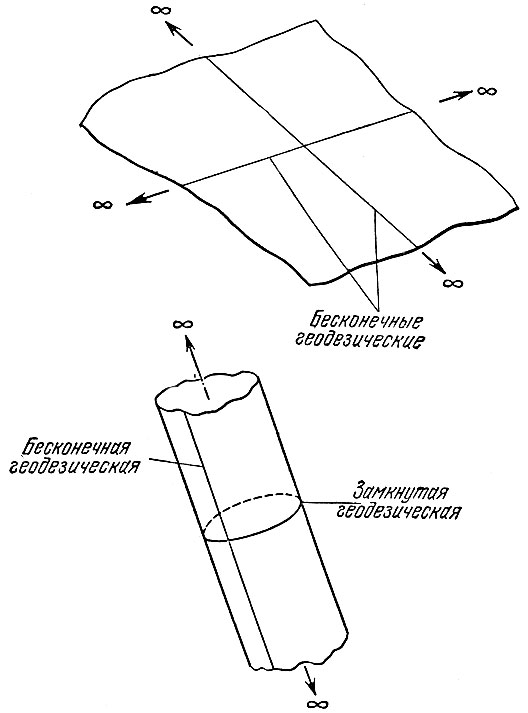
Рис. 19. Плоскость, простирающаяся до бесконечности и бесконечный цилиндр - две безграничные поверхности с одинаковой кривизной c = О, но с разными топологическими свойствами

К обсуждению этого очень важного вопроса мы еще вернемся в последнем разделе книги (см. § 6 гл. 5).

Сейчас еще раз подчеркнем, что в простейших, наиболее естественных вариантах топологии в случае ρ ≤ ρ_крит мир пространственно бесконечен, в случае ρ > ρ_крит мир неизбежно замкнут, конечен.