§ 4. Средняя плотность вещества во Вселенной и наблюдательное исследование кривизны пространства

Кривизну трехмерного пространства можно определить вычислением, зная постоянную Хаббла и плотность вещества. Но, к сожалению, плотность вещества; как мы видели выше, известна столь плохо, что не определен даже знак кривизны пространства - положительна она или отрицательна.

А нельзя ли обратить задачу? Нельзя ли измерить кривизну пространства и уже по кривизне вычислить плотность ρ? При этом автоматически будет определено р с учетом видов вещества - и трудно наблюдаемого и легко наблюдаемого. Один путь исследования кривизны - это наблюдение зависимости m ÷ z для очень далеких галактик (или квазаров). Вычисления по формулам релятивистской космологии показывают, что для далеких объектов зависимость m ÷ z должна отклоняться от прямолинейной зависимости, которая была нами описана в гл. 1 в рамках классической механики и электродинамики. Отклонение от прямой линии зависит от кривизны пространства. На рис. 20 а нанесены разные кривые, соответствующие разной кривизне и, следовательно, разной плотности ρ. Из рисунка видно, что данные наблюдений не позволяют пока определить, больше ли ρ, чем ρ_крит или нет? Другой способ определения кривизны пространства состоит в подсчетах галактик (или радиоисточников) до данной видимой звездной величины. Эта зависимость должна быть разная для пространств с разной кривизной. При этом истинная яркость галактик считается известной, или хотя бы постоянной для разных объектов. На пути таких исследований имеется много технических трудностей. Но помимо трудностей технических, существует принципиальная трудность. От далеких источников мы наблюдаем свет, испущенный давно, т. е. это свет, испущенный объектами, находящимися на более ранней стадии развития по сравнению с близкими объектами. Поэтому прежде чем определять ρ из графиков типа риc. 20а, надо учесть эволюцию галактик - изменение их светимости, спектра и т. п. Как эволюционируют галактики, практически совсем не известно, и выводы о значении ρ остаются очень неопределенными.

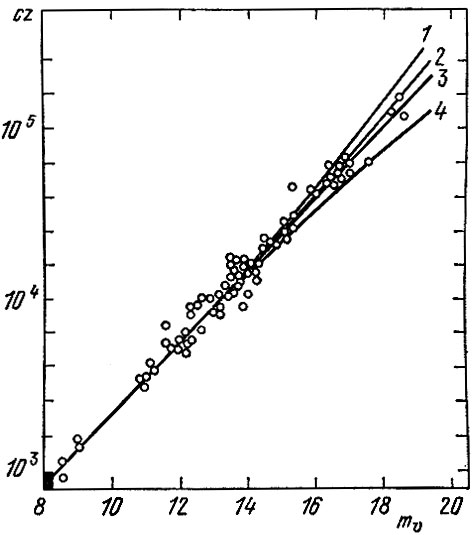
Рис. 20 а. Зависимость m ÷ z с теоретическими кривыми для разной плотности 1) ρ = 10 ρ_крит; 2) ρ = 5 ρ_крит; 3) ρ = 2 ρ_крит; 4) кривая, соответствующая теории стационарной Вселенной; см. § 5 гл. 5

Большие надежды в космологии возлагались на радиоастрономию. Чувствительность радиотелескопов огромна. Однако оказалось, что радиоизлучение галактик меняется со временем еще сильнее, чем оптическое излучение, и радиоастрономия также не дала решения проблемы кривизны пространства. Этот вопрос продолжает стоять на повестке дня науки.

Отметим любопытное явление, которое должно наблюдаться в однородной Вселенной. Пусть мы наблюдаем в обычном пустом плоском пространстве объекты одинакового линейного размера (например, одинаковые галактики), находящиеся на разных расстояниях. Чем дальше объект, тем меньше угол, под которым мы видим объект (рис. 20 б). Угловой размер объекта будет обратно пропорционален расстоянию.

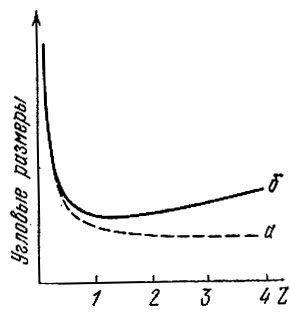
Рис. 20 б. Зависимость углового размера объекта от красного смещения: а) когда в конусе лучей нет вещества; б) когда в конусе лучей есть вещество

Иная картина должна наблюдаться в пространстве в среднем равномерно заполненном прозрачным веществом, например, прозрачным газом или перекрывающимися коронами галактик. Из общей теории относительности известно, что лучи света, проходящие вблизи тяготеющих масс, отклоняются ими, притягиваются. Таково знаменитое отклонение на 1",75 лучей света звезд, когда лучи проходят вблизи поверхности Солнца. Поэтому газ, находящийся в конусе лучей от далеких галактик, будет изгибать их, как схематически показано на рис. 20 б. Чем дальше объект, тем большая масса содержится в конусе лучей, тем больше отклонение. Это приводит к тому, что, начиная с некоторого расстояния, более далекий объект имеет уже не меньшие угловые размеры, а большие, чем более близкий! Разумеется, этот эффект будет иметь место только тогда, когда в конусе лучей есть газ (или другая материя). Если же вещество сосредоточено только в галактиках, межгалактическое пространство пусто и в конусе лучей совсем нет вещества, то даже несмотря на высокую среднюю плотность галактик, в пространстве для пустого конуса лучей этот эффект отсутствует. На это обстоятельство обратил внимание Я. Б. Зельдович.