28. Запуск спутника вручную

А Можно ли запустить искусственный спутник Земли без ракеты, так сказать, вручную, за счет своей мускульной силы?

Б Надо подняться на башню, описанную в задаче 17. Подняться можно (в принципе) за счет мускульной силы, правда, при условии, что на каждом километре высоты имеется столовая, а через каждые три - пять километров - гостиница. Ну и, разумеется, при условии, что уже есть сама башня. Поскольку при строительстве башни можно обойтись без ракет, то использование башни не противоречит условиям задачи.

На какую же высоту надо подняться? Если вы считаете, что нужно подняться на высоту H = 35 800 км, то вы правы лишь отчасти. Отпустив на этой высоте (точка Д башни Б, в плоскости рис. 19 - экваториальное сечение Земли) какой-нибудь груз, вы превратите его в спутник с круговой орбитой и 24-часовым периодом обращения. Радиус такой орбиты равен H + R₀ ≈ 35 800 + 6380 = 42 180 км, где R₀ - радиус Земли. При этом спутник все время будет висеть рядом с вами (если вы, отпуская его, не придали ему руками дополнительной скорости). Но от вас не требовалось создания такого высокого спутника. С какой минимальной высоты можно запустить спутник вручную?

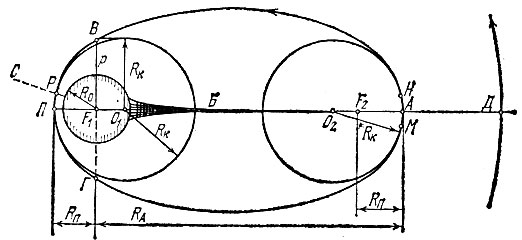
Рис. 19

В С меньшей высоты спутник с круговой орбитой вручную запустить нельзя (мы пренебрегаем той добавочной скоростью, которую ваши руки могут придать спутнику). Но можно придать ему эллиптическую орбиту. Поскольку линейной скорости башни (вращающейся вместе с Землей) на меньших высотах (точка А) недостаточно для круговой орбиты, то отпущенный предмет будет падать на Землю. Но упадет ли? Ведь башня придает ему горизонтальную составляющую скорости.

Как ясно из предыдущих задач, точка отпускания спутника будет апогеем А его орбиты. Высота отпускания должна быть такой, чтобы перигей П орбиты оказался не внутри земного шара. Зададимся допустимым расстоянием перигея от центра Земли порядка (R_П)_доп = 7000 км (с запасом на толщину атмосферы и на погрешности расчетов на логарифмической линейке). Теперь остается вычислить апогейное расстояние R_A.

Для расчета можете использовать данные предыдущих задач, а недостающие сведения взять, например, в журнале "Квант" (№ 11 за 1974 г. и № 2 за 1975 г.). Здесь мы, чтобы не повторяться, применим несколько иной метод. Этот метод не проще и не точнее других и, кроме того, требует от вас некоторых дополнительных знаний, но он менее стандартен, а знать нестандартные методы намного полезнее, чем еще раз воспользоваться стандартным. Воспользуемся тем, что эллипс обладает симметрией относительно своих большой и малой осей. В силу симметрии кривизна эллипса в апогее и перигее должна быть одинакова. Требуемый радиус кривизны R_K в перигее нам задан перигейным расстоянием (R_П)_доп = 7000 км (но не равен ему, а зависит также и от R_A). Мы будем задаваться величиной R_A и вычислять соответствующие ей R_K и R_П. Если при этом окажется, что R_П ≥ (R_П)_доп, то задача будет решена.

Кругом кривизны в точке А кривой называется предельное положение круга, окружность которого проходит через А и две другие бесконечно близкие точки кривой H и М, когда H → А и М → А (рис. 19). Радиус кривизны кривой в точке А есть радиус R_K круга кривизны. Центр кривизны для точки А есть центр этого круга 02, он лежит на нормали к кривой в точке Л. В силу симметрии эллипса радиусы кривизны для апогея А и перигея П одинаковы. Из свойств эллипса известно, что для точек А и П

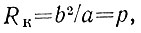
(1)

где а и b - большая и малая полуоси эллипса, р - его фокальный параметр (половина хорды ВГ, проведенной через фокус F_i перпендикулярно к большой оси, см. рис. 19). Эксцентриситет эллипса

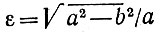
(2)

и, с другой стороны,

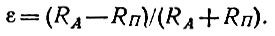
(3)

Возводя формулу (2) в квадрат, подставляя в нее (1) и (3), получаем

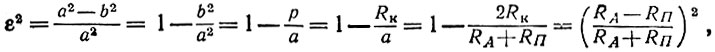
откуда

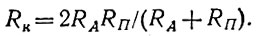
(4)

Задаваясь определенным RA и вычисляя для него R_K (некоторым независимым образом), мы из формулы (4) можем вычислить R_П:

(5)

Зададимся R_A = 30 000 км и рассмотрим поведение предмета, отпущенного в точке А. Ускорение свободного падения g обратно пропорционально квадрату расстояния от центра Земли (здесь R₀ - радиус Земли, g₀ - ускорение свободного падения на ее поверхности):

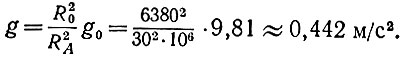
(6)

Начальная горизонтальная скорость отпущенного предмета равна скорости точки А башни (здесь Ω - угловая скорость вращения Земли и башни, стоящей на экваторе):

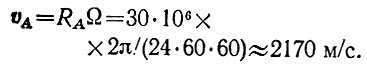
(7)

А теперь главное. Ищем радиус кривизны в точке А. В момент t₀ = 0 отпускаем предмет из рук. Если бы не было тяготения, то он полетел бы равномерно и прямолинейно по касательной к окружности, которую описывает точка А вращающейся башни (рис. 20). В течение t = 1 с он пролетел бы

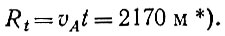
(8)

^*) (Поскольку однако, башня продолжает вращаться, то от башни предмет не касаться, а только приподнялся бы на 8 см (настолько точка, движущаяся по касательной, отодвинется за секунду от окружности, с которой она сорвалась).)

Наличие земного тяготения заставит предмет опуститься по направлению к центру Земли на

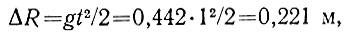
(9)

в результате чего он окажется в точке Н (рис. 20).

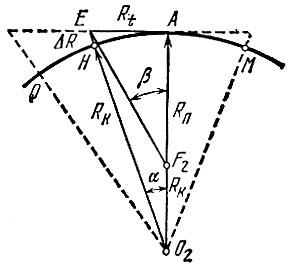
Рис. 20

Сделаем важную оговорку. На рис. 20 отрезок Δ R отложен по направлению к O₂, т. е. к центру кривизны, а не к центру Земли F₁. Это неправильно, но погрешность ничтожна. Углы на рис. 20 сильно преувеличены: если за сутки башня совершает один оборот, то за час она поворачивается на 15°, за минуту - на 15', за секунду - на 15". Углы α и β ненамного больше. Поскольку искомое перигейное расстояние порядка 7000 км, то β будет порядка 1', и разницей в направлениях на F₁, на 0₂ и на F₂ можно пренебречь.

Итак, мы имеем две точки А и Ну лежащие на окружности кривизны, радиус R_K которой мы ищем. Для построения окружности нужна третья точка. Ее можно получить либо как положение Q предмета через t = 2 с, либо как точку М, положение которой нам уже известно из соображений симметрии. В первом случае мы найдем кривизну для средней точки Н, во втором - для искомой Л, однако при столь малых t это практически одно и то же. По Определению круга кривизны точки Н и М должны быть бесконечно близкими к А. Чтобы обойтись без дифференциального исчисления, мы берем точки не бесконечно близкие, а очень близкие к A. То, что вытекающая отсюда погрешность ничтожна, легко проверить: вычислив R_K при t = 1 с, можно повторить вычисления для t = 100 с; при этом погрешность от конечности t все еще не превосходит погрешности логарифмической линейки. Это позволяет считать нижеследующие расчеты R_K приемлемыми по точности.

Из прямоугольного треугольника ЕА0₂ следует, что

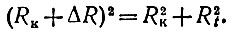
Раскрывая скобки и пренебрегая слагаемым ΔR² << 2R_КΔR, имеем

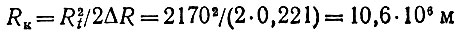
(10)

и, согласно (5),

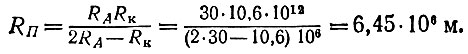
Это лишь на 80 км больше радиуса Земли, и, следовательно, предмет, отпущенный с точки А при R_A = 30 000 км, пойдет по эллипсу, огибающему Землю на высоте h = 80 км, т. е. сгорит в плотных слоях атмосферы и спутником не станет. Итак, мы немножко не угадали правильное R_A.

В качестве второй попытки выбираем несколько большее R_A = 30 500 км. Теперь, согласно формулам (6)-(10), имеем

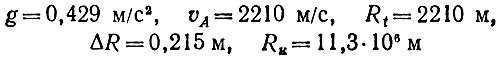
и, следовательно,

Задача решена. Наименьшее R_A ≈ 30 500 км, что соответствует высоте над поверхностью Земли

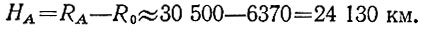
Сверим наше решение с традиционным, которое опирается на закон сохранения энергии. Для спутника, не растрачивающего энергию на трение и др., этот закон записывается как постоянство суммы кинетической и потенциальной энергий:

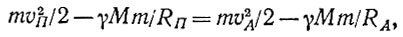
(11)

где m и М - массы спутника и Земли, γ - универсальная гравитационная постоянная, γM = 3,97*10^14м3/_с². Из второго закона Кеплера следует, что

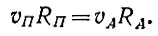
(12)

С учетом этого формула (11) дает v²_A(R_A + R_П) = 2γM ^R_П/_RA, или

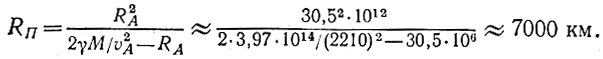
Таким образом, энергетический метод и метод, основанный на радиусе кривизны, эквивалентны.

Итак, поднявшись на высоту 24 130 км (8 000 001-й этаж), можно смело бросаться вниз головой (в скафандре). Через 7 ч (3-й закон Кеплера) вы пронесетесь над Землей на высоте 630 км -и затем снова вознесетесь туда, откуда вы нырнули в космос. И через 14 ч вы легко и непринужденно, с относительной скоростью, равной нулю, вернулись бы на все тот же этаж башни, если бы башня оставалась на месте. Но ее там уже нет и встретитесь вы с нею на месте старта только через 7 суток (в конце 12-го витка), если Луна за это время не повернет вашу орбиту так, что вы проскочите мимо башни.

Впрочем, нет! Вы встретитесь с ней намного раньше. За 35 ч вы совершите 2,5 оборота, а башня - чуть-чуть меньше 1,5 оборота. Следовательно, незадолго перед этим, примерно через 34 ч после старта, число оборотов ваше и башни будет различаться ровно на один оборот. Это значит, что вы встретитесь с ней недалеко от перигея (в точке Р на башне СР, показанной на рис. 19 пунктиром). Скорость башни в точке Р в ^R_A/_RП раз меньше, чем в А, т. е. порядка 500 ^м/_с. Ваша скорость - в то же число раз больше, чем в А, т. е. около 9500 ^м/_с. Поэтому ваша встреча с башней не будет легкой и непринужденной. Вам следует позаботиться о своем спасении несколько раньше. Пожалуй, до того, как вы прыгнете с башни^*).

^*) (А хорошо бы, прыгая с RA =30 000 км и входя в плотные слои атмосферы, Применить крылья, с помощью которых можно постепенно гасить свою космическую скорость (то погружаясь в атмосферу и нагреваясь, то рикошетируя от нее в вакуум и остывая), а затем на парашюте мягко приземлиться! То-то нам позавидовали бы прыгуны в воду, прыгуны с трамплина, прыгуны на батуте, прыгуны о парашютом и прыгуньи через веревочку!)

И вообще эта башня - дьявольское изобретение. Вращаясь в экваториальной плоскости, она будет сшибать все, что встретится на ее пути. А поскольку орбита любого спутника пересекает экваториальную плоскость, то рано или поздно все спутники, высота орбиты которых меньше высоты башни, будут ею сбиты. У подножья башни будут лежать обломки почти всей космонавтики.

Итак, по-видимому, прежде чем строить башню, надо сделать выбор: космонавтика или башня. Выбор произошел уже сам собой: техника созрела для космонавтики гораздо раньше, чем она созреет для башни.