29. От полюса к полюсу

А Спутник выведен на круговую полярную орбиту, т. е. такую, в плоскости которой находятся оба географических полюса. Как выглядит проекция его орбиты на поверхность земного шара?

Б Многие утверждают, что проекция орбиты спутника совпадает с тем меридианом, вдоль которого он движется. Но тогда второй виток, как продолжение первого, должен проходить по тому же меридиану.

Другие, учитывая, что плоскость орбиты спутника должна быть неподвижной в пространстве, а Земля вращается вокруг своей оси, проходящей через полюсы, считают, что спутник пересекает все меридианы под некоторым углом. Но тогда возникают парадоксы: как можно уйти с полюса под углом к меридианам, если все направления с полюса - меридианы? И гак спутник попадет с Северного полюса на Южный?

Встречается и такой контрвопрос: а обязательно ли спутнику, проходящему над Северным полюсом, попадать еще и на Южный? Обязательно! По первому закону Кеплера плоскость орбиты спутника содержит центр Земли. Если к тому же эта плоскость содержит в себе и один из полюсов, то она содержит и весь отрезок полюс - центр, на продолжении которого находится второй полюс.

Чтобы задача стала нагляднее, представьте, что Земля строго шарообразна (с радиусом r₀) и оклеена белой бумагой (как глобус), а спутник летит на высоте, равной нулю, и вертикально вниз с него направлен карандаш, который чертит на бумаге его след. И пусть при этом трение карандаша о бумагу никак не сказывается ни на ориентации карандаша, ни на скорости спутника.

В Начнем с момента пролета спутника над Северным полюсом. Спутник С движется вдоль некоторого меридиана М₀ (рис. 21) со скоростью v_с ≈ 8 ^км/_с, а Земля под ним поворачивается с угловой скоростью

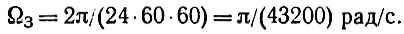
(1)

Спустя время t спутник С оказывается на некоторой широте Θ, продвинувшись от полюса на угол γ = ^π/₂ - Θ. Радиус малого круга параллели Θ равен

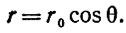
(2)

За счет вращения Земли меридиан М₀ отойдет от спутника С на восток (для земного наблюдателя, стоящего на М₀, спутник отойдет на запад) на величину дуги малого круга

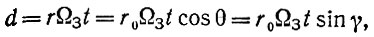
(3)

где Ω_Зt - длина этой дуги в радианах. Угол γ есть отношение дуги L к ее радиусу:

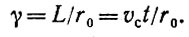
(4)

Таким образом, окончательно, согласно (3) и (4),

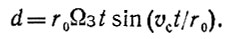
(5)

На рис. 21 жирной линией, ориентировочно показана кривая, которую, прочертит полярный спутник на поверхности вращающегося земного шара за время первого полувитка (в горизонтальном направлении масштаб кривой преувеличен примерно вдвое). Спутник начинает свое движение от полюса строго по меридиану, но тут же, за счет вращения Земли, начинает и отклоняться, сначала еле заметно (мала линейная скорость уходящего от спутника меридиана), затем все быстрее. Наибольшая скорость расхождения спутника и меридиана (линейная скорость поверхности Земли v_З) - на экваторе:

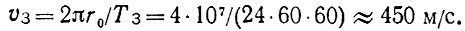
(6)

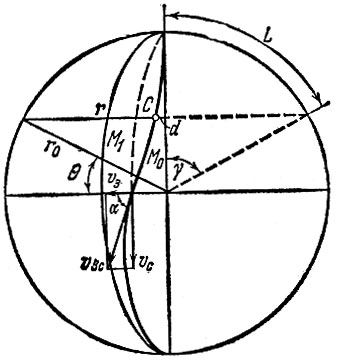
Рис. 21

Угол α, под которым траектория спутника пересекает экватор, можно найти из прямоугольника скоростей (см. рис. 21): tgα = ^v_c/_vЗ что для спутника на нулевой высоте дает

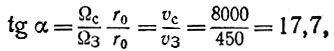
откуда α ≈ 86°45'. После экватора v_З вновь убывает, и траектория спутника вблизи Южного полюса идет почти точно по меридиану M₁ отличному от начального М₀ на угол поворота Земли за время, соответствующее полувитку спутника:

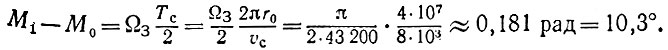
(8)

В малой окрестности полюса, где sinγ ≈ γ формула (5) дает

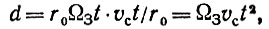
(9)

т. е. начальная часть траектории является параболой, касающейся меридиана (при условии, что соответствующий участок шаровой поверхности удалось бы распрямить на плоскости без разрывов).

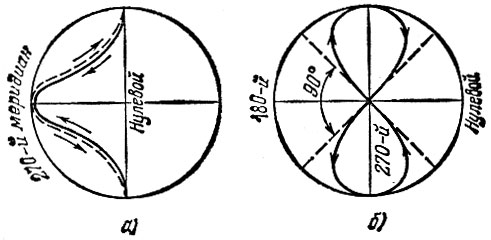
Рис. 22

В случае полета на высоте Н > 0 нужно рассматривать поведение на поверхности Земли не спутника, а подспутниковой точки (точки, для которой спутник находится в зените). Чем больше H, тем меньше орбитальная скорость спутника. Угловая же скорость (относительно центра Земли) подспутниковой точки

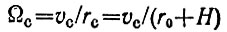
(10)

убывает еще быстрее, так как в формуле (10) не только убывает числитель, но еще и растет знаменатель.

Любопытно поведение кругового спутника с радиусом орбиты r = 42 180 км. За сутки (звездные) он совершает ровно один оборот. Если он движется поэкваториальной орбите попутно с Землей (на восток), то земному наблюдателю кажется висящим неподвижно над некоторой точкой экватора, так как Ω_C = Ω_З. Если же его вывести на полярную орбиту, то, начиная свое движение, например, от полюса по нулевому меридиану, за четверть оборота он достигает экватора и пересекает его на 90° западнее под углом

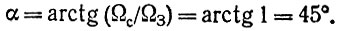
К Южному полюсу он подходит по 180-му меридиану (рис. 22, б), после чего уходит от полюса вновь по нулевому меридиану (являющемуся продолжением 180-го). Продолжая отклоняться от него по-прежнему к западу, спутник пересекает экватор в той же точке от экватора до экватора спутник совершил пол-оборота в полярной плоскости, а Земля за это время - тоже пол-оборота в экваториальной и подставила под спутник ту же самую точку. В результате на Земле подспутниковая точка за один оборот описывает "восьмерку", пересекая на экваторе свою собственную траекторию под углом 90°. На рис. 22, а показан вид этой траектории сбоку; сплошной линией показано движение подспутниковой точки на ближней к нам стороне земного шара, пунктирной - на обратной (пунктир должен совпадать со сплошной линией)^*).

^*) (Более подробно с поведением подспутниковой точки для спутников разной высоты и наклонения можно познакомиться по книге: Штернфельд Л. Искусственный спутник, 2-е изд.- М.: Гостехиздат, 1958.)