51. Винт самолета в кино

А Вы с приятелем смотрите кино. В кадре - самолет, выруливший на взлетную полосу. Двухлопастный винт самолета пришел в движение. Сейчас самолет начнет разбег для взлета.

- Винт в данный момент делает 11,5 ^об/_с,- солидно, со знанием дела заявляет ваш приятель.

Откуда он может это знать, да еще с такой точностью? Может быть, он это сказал безответственно, только потому, что его никак нельзя проверить?

- Позвольте, вы ошибаетесь!..

Козьма Прутков "Опрометчивый турка".

Б Ваш приятель мог вычислить число оборотов винта. Можете сделать это и вы, если предварительно разберетесь в том, как будет выглядеть винт, совершающий число оборотов в секунду N, равное числу кинокадров в секунду n. Для простоты начните с однолопастного винта (хотя в авиации таких винтов и не бывает - центробежная сила инерции не была бы уравновешена и изогнула бы вал). Для справки: киносъемка производится обычно со стандартным числом кинокадров в секунду n = 24.

Проанализировав этот случай, рассмотрите поведение изображения однолопастного винта, совершающего N = n + 1 = 25 ^об/_с и N = n - 1 = 23 ^об/_с. Потом вы войдете во вкус и уже сами во всем разберетесь.

- Я ошибаюсь?! Ни за что!.. 

Козьма Прутков "Черепослов" (оперетта).

В Представим для простоты, что киносъемка винта ведется с предельно короткой выдержкой, и поэтому снимок винта на каждом кадре получается четким, несмотря -на быстрое вращение. Пусть на первом кадре лопасть винта оказалась вертикальной. Поскольку N = n, то к моменту съемки второго кадра лопасть, совершив целый оборот (дуга α₁ = 360° на рис. 61, а), опять окажется в вертикальном положении. Все промежуточные положения не будут сняты, так как лопасть прошла через них при закрытом затворе кинокамеры. То же повторится в третьем (дуга α₂) и последующих кадрах, В результате лопасть на всех кадрах будет представлена кинозрителю в одном и том же положении, и зритель, естественно, будет считать ее неподвижной. Если, однако, он так же сообразителен, как ваш приятель, то примет во внимание, что перед этим лопасть пришла в движение и непрерывно набирала обороты. Следовательно, сейчас она на самом деле вращается, совершая N = n = 24 ^об/_с.

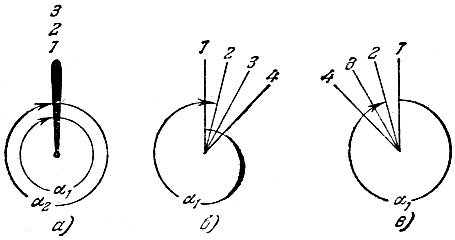
Рис. 61

Рассмотрим поведение изображения при N = 25 ^об/_с (лопасть по-прежнему вращается по часовой стрелке). Если в первом кадре она заснята в вертикальном положении 1 (рис. 61, б), то ко второму кадру (за ¹/₂₄ с) она совершит ²⁵/₂₄ = 1 + ¹/₂₄ об (дуга α₁ = 375°), и во втором кадре она будет снята с отклонением вправо от вертикали на 15° (прямая 2 на рис. 61, б). В третьем кадре она будет зафиксирована еще правее.

Легко сообразить, что, поворачиваясь от кадра к кадру на 15°, изображение лопасти за 24 кадра (т. е. за 1 с) совершит один оборот и тоже по часовой стрелке. Таким образом, в то время как сама лопасть совершает 25 ^об/_с, ее изображение на кинопленке совершает 25 - 24 = 1 ^об/_с. Следить за таким медленным вращением, оценить кажущуюся его скорость и определить по ней истинную совсем нетрудно. Интересно, что если лопасть совершает 23 ^об/_с, то зритель увидит ее вращающейся также со скоростью 1 ^об/_с, но против часовой стрелки, т. е. в направлении, противоположном истинному направлению вращения (рис. 61, в).

В самом деле, в интервале между кадрами она поворачивается на ²³/₂₄ об по часовой стрелке. Но зритель этого не видит. Он видит, что во втором кадре лопасть оказалась на ¹/₂₄ об левее, чем в первом, в третьем - еще на ¹/₂₄ об левее, чем во втором, и т. д. Связывая эти последовательные образы по кратчайшему расстоянию, зрительный аппарат создает впечатление медленного вращения против часовой стрелки.

Проследим теперь за поведением изображения лопасти в течение всего времени, пока она набирает скорость от 0 до 24 ^об/_с. Неподвижная лопасть изображается неподвижной. Пока число ее оборотов невелико "(1-5), зритель успевает следить за изображением, С дальнейшим увеличением оборотов зритель уже не успевает следить за лопастью, хотя ее изображение правильно отображает ее движение. Так будет до тех пор, пока N не нарастет до ⁿ/₂ = 12 ^об/_с. Тогда лопасть между кадрами поворачивается ровно на полоборота, и по кинокадрам нельзя определить, в какую сторону она совершает эти полоборота. При 24 > N > 12 она совершает между кадрами более чем пол-оборота и представится вращающейся в противоположном направлении, причем с увеличением истинного числа оборотов кажущееся числе уменьшается. Наконец, при N = 24: кажущееся число будет N' = 0. Лопасть кажется неподвижной. Связь между N и N' показана на рис. 62 ломаной ОАВ.

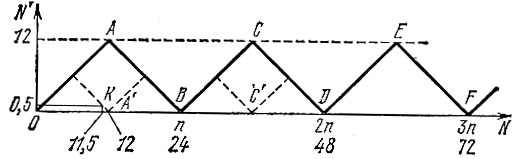
Рис. 62

А что же дальше? Дальше ломаная периодически, повторяется: когда N дорастет до 2n, лопасть между кадрами будет успевать совершить ровно два оборота и на съемку будет являться каждый раз в одном и том же положении. Поэтому при N = 2n она опять будет казаться неподвижной (N'= 0, точка D). То же будет при N = 3n, 4n и т. д.

Отличить ситуацию F от ситуации В можно только при внимательном слежении за поведением изображения с самого начала вращения и при подсчете числа переходов изображения через неподвижное состояние. Третье неподвижное состояние означает, что число оборотов в секунду в действительности равно 3n = 3*24 = 72. На практике, поскольку при съемке затвор открывается на конечное время, то лопасть на снимке оказывается несколько размазанной. Изображение лопасти при N = 3n отличается от изображения при N = n тем, что размытость лопасти втрое больше.

Вы с приятелем наблюдали в фильме не одно-, а двухлопастный винт. Он будет казаться неподвижным, очевидно, при N = ⁿ/₂, n, ³ⁿ/₂, 2n, ... (точки А', В, С' пунктирной ломаной на рис. 62), так как для двухлопастного винта достаточно повернуться между кадрами на полоборота, чтобы два смежных кадра стали неразличимыми. Правда, если лопасти окрашены в разные цвета, то остается в силе первоначальная сплошная ломаная. Ваш приятель видел винт вращающимся со скоростью один оборот в две секунды в направлении, противоположном истинному (точка К на рис. 62), когда он заявил, что число оборотов равно 11,5.

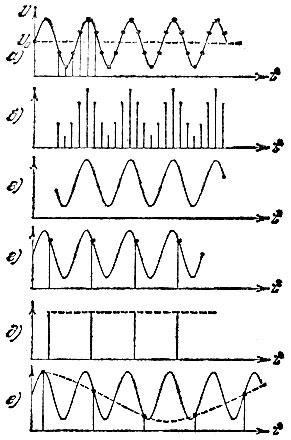
Рис. 63

В заключение заметим, что рассмотренные здесь искажения информации о движении и график OABCDE рис. 62 имеют большое значение не только для кино и светотехники (задача 49), но и в любом случае, когда какое-нибудь непрерывное колебание наблюдается прерывисто. Если на вход линии связи поступает синусоидальное колебание частоты N, но по линии связи передаются только его отдельные (дискретные) значения с частотой n (т. е. п коротких импульсов в секунду, каждый из которых имеет амплитуду, равную соответствующему мгновенному значению непрерывного колебания), то по этим отдельным значениям можно полностью и безошибочно восстановить непрерывное колебание на приемном конце линии только при условии, что N < ⁿ/₂, т. е. что на каждый период синусоидального колебания приходится не менее двух передаваемых значений. В этом состоит смысл (здесь несколько упрощенный) одной из фундаментальных теорем теории информации - теоремы Котельникова.

На рис. 63, а показан электрический сигнал (зависимость напряжения U от времени t), подлежащий передаче по линии связи. Он состоит из синусоиды и постоянной составляющей напряжения U₀. Пусть по линии связи передаются только те значения сигнала, которые отмечены точками (по шесть значений на период синусоиды). Иными словами, по линии связи передаются импульсы, показанные на рис. 63, б. Приняв и должным образом продетектировав их, мы получим огибающую (рис. 63, в), в точности повторяющую первоначальный непрерывный сигнал. Стоит, однако, нарушить требование теоремы Котельникова, как сигнал восстановить уже не удастся. На рис. 63, г показан случай, когда по линии связи передается по одному импульсу за период сигнала (n = N, точка В на рис. 62). На выходе линии будут приняты импульсы постоянной амплитуды (рис. 63, д), их огибающая (пунктир) совершенно не отражает форму передаваемого сигнала.

Если пойти еще дальше и взять n < N, то в огибающей импульсов вновь появится синусоида (пунктир рис. 63, е), но частота её будет далеко не равна первоначальной (сплошная кривая рис. 63, е). Эту частоту можно определить по графику рис. 62.

Теория информации имеет множество практических применений: проводная и радиосвязь, телеметрия, радионавигация, гидролокация, телевидение, кино, вычислительная техника и т. д. И везде для неискаженной передачи или обработки информации требования теоремы Котельникова должны быть соблюдены.