52. Порядок среди беспорядка

А Перед вами фотография диска с нанесенными на нем одинаковыми черными кружками (рис. 64). Впечатление такое, что в расположении кружков нет никакого порядка. Однако на самом деле здесь есть несколько кружков, нанесенных строго закономерно, равномерно по окружности диска. Найдите этот порядок среди беспорядка.

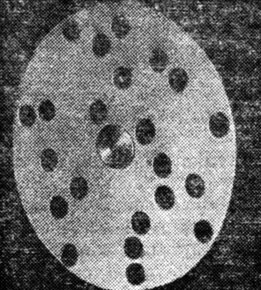
Рис. 64

Б Если вы не придумаете ничего лучшего, чем вооружиться циркулем и чертить концентрические окружности, то задача вам наскучит раньше, чем вы доведете ее до конца. Кстати, чтобы удержать вас от этого примитивного пути, диск умышленно снят наискосок. Чтобы вас заинтриговать, придется немного приоткрыть карты. Взгляните на фотографию, приведенную на рис. 65. Она снята с того же диска и отчетливо показывает шесть упорядоченных кружков ("сигналов") на фоне хаоса ("помех"). Как получена эта фотография?

Считайте, что на обоих фото вы видите не позитивы, а негативы истинного диска.

В Судя по тому, что шесть упорядоченных кружков оказались густо-черными, а остальные - бледно-серыми, выдержка при фотографировании первых была больше, чем при фотографировании остальных. Но ведь невозможно для одних кружков затвор фотоаппарата открыть на большее время, а для других - на меньшее, тем более что пока не известно, для каких именно кружков это надо делать. Видимо, сами кружки каким-то образом управляли выдержкой для себя. Кстати, серых кружков на рис. 65 оказалось в несколько раз больше, чем их было на первоначальном рис. 64. Так могло получиться, если кружки экспонировались на один и тот же кадр в нескольких положениях. Следовательно, диск во время съемки вращался.

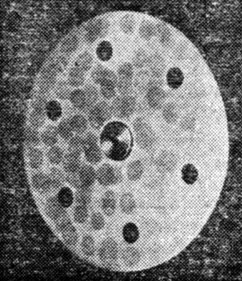
Рис. 65

Но это еще не ответ. Если бы диск вращался, пока открыт фотозатвор, то на снимке каждый кружок размазался бы в дугу, как это произошло со звездами в задаче 6. Видимо, за время съемки затвор открывался на короткие мгновения несколько раз... Все ясно!! Ну и ловкач же фотограф! Он снял диск на один кадр шесть раз, поворачивая его между съемкой каждый раз на 60°. И поэтому все кружки, расположенные упорядочение через 60°, экспонировались 6 раз точно на место своих предшественников и получились яркими (т, е. на негативе густо-черными), а беспорядочные экспонировались каждый раз на новое место и получились в шесть раз бледнее, причем их число на снимке возросло в шесть раз.

Как ни лестна фотографу похвала, но ему следует без ложной, скромности признаться, что он еще больший ловкач, чем вы думаете. Легко вам назвать цифру 60°, когда вы видите готовенький результат - второе фото. А как фотограф узнал, что диск между съемками нужно поворачивать на 60°? Ведь для этого надо знать, что число упорядоченных кружков равно шести, а не пяти, не четырем... Ладно, поскольку вы уже немало потрудились, остальное можно раскрыть.

Диск действительно вращался. Но, кроме того, во время съемки его освещали прерывистым светом (прерывистый свет можно получить и от непрерывного источника, Солнца, например, если на пути его лучей поставить вертушку с непрозрачными лопастями). За один оборот диск освещался шесть раз короткими, почти мгновенными вспышками. Фотозатвор же был открыт в течение всего оборота, что в сочетании со вспышками света равносильно угаданному вами периодическому открыванию затвора шесть раз.

Ну, а как фотограф узнал, что частота вспышек должна быть. ровно в шесть раз выше частоты вращения диска? Очень просто: он перепробовал все варианты. Просто? Да, просто, если механизировать выбор варианта. Надо менять частоту вращения вертушки от нуля на повышение при постоянной частоте вращения диска. При этом диск будет виден то вращающимся, когда частоты не кратны, го неподвижным, когда они кратны (см. задачу 51). В частности, при равных частотах диск кажется неподвижным в своем естественном виде, как на рис. 64 (первая слепая скорость), т. е. все кружки одинаково черны.

Увеличивая частоту вертушки (стробоскопа) вдвое, мы обнаружим, что шесть кружков ярче других, а остальные раздвоились и стали вдвое бледнее; при трехкратном соотношении частот шесть кружков вновь обнаружились, а остальные стали бледнее втрое и число их утроилось. При четырех- и пятикратном соотношениях частот картина менее выразительна. А при шестикратном^ будет достигнут максимальный контраст картины - шестикратный. Раздробить помеху более чем в шесть раз (без раздробления сигнала) не удастся: 12-, 18-, 24-кратное соотношения дадут тот же шестикратный контраст.

Вернувшись к 6-кратному соотношению, сделаем вращение вертушки равномерным и сфотографируем диск. И вот результат: периодическая структура четко видна на фоне случайных помех.

Имеет ли это явление практическое применение? Чрезвычайно широкое. Кино, телевидение, связь, радиолокация используют этот принцип на каждом шагу. Но мы начнем с наиболее наглядного примера, хотя область его применения ограничена.

Представьте, что археологи нашли тарелку, расписанную древним художником. На ней столько царапин и пятен, что узор не обнаруживается. Вы уже догадались, что над этой тарелкой стоит провести описанный выше эксперимент (только вращать ее не следует: нельзя рисковать уникальной находкой, лучше привести во вращение ее фотографию). Если в узоре есть симметрия относительно центра вращения, то она будет обнаружена.

Теперь пример из кино. Пусть в течение хотя бы одной секунды нам показывают неподвижный пейзаж. Это значит, что изображение (полезный сигнал) во всех соседних 24 кадрах одинаково. Но, кроме изображения, в каждом кадре имеются дефекты: зернистость пленки, царапины, прилипшие пылинки. Все эти дефекты в каждом кадре глубоко индивидуальны, случайны. На экране за секунду мы увидим 24 раза одинаковые полезные сигналы и только один раз каждый из дефектов, которые неодинаковы и появляются вразнобой по времени и месту. Это существенно улучшает отношение сигнала к помехам. Изображение в кино кажется намного чище, чем мы его видели бы, разглядывая отдельный кинокадр,- вы это сами можете проверить, когда из-за неисправности кинопроектора на экране остановится один кадр.

То же самое имеет место в телевидении: сигналы в смежных кадрах (для неподвижных объектов) одинаковы, а случайные "снежинки" помех различны. Инерционность нашего зрительного восприятия поможет.накопить впечатление от сигнала с нескольких кадров, и он будет виден лучше, чем помехи.

Заметим, что это только малая часть той пользы, которую извлекают в телевидении из принципа накопления. Более фундаментально накопление используется на передающем конце, в телевизионной передающей трубке, где первоначальное малое отношение сигнала к помехам улучшается за счет накопления приблизительно в миллион раз.

И, наконец, пример из радиолокации (рис. 66). Рассмотрим его. несколько глубже, так как он универсален и имеет большое значение для всех областей техники, связанных с теорией информации. Впрочем, тот, кто устал, может его пропустить.

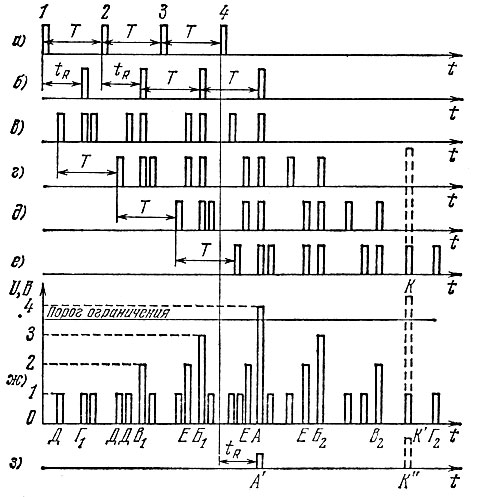
Рис. 66

Пусть радиолокатор посылает четыре зондирующих импульса, (лента а), следующих друг за другом с определенным периодом Т. От облучаемого объекта вернутся четыре отраженных импульса (лента б), следующих с тем же периодом Т, но запаздывающих каждый относительно своего зондирующего на время t_R. Измерив это запаздывание, мы измерим расстояние до отражающего объекта.

Теперь представьте, что вместо сигналов (б) вы получили смесь сигналов и помех (лента в). Задача измерений сильно осложнилась бы: все импульсы одинаковы; какие из них полезные, какие помехи - на первый взгляд отличить невозможно.

Попробуем применить только что освоенный нами принцип накопления. Запишем принятые сигналы (в) на четырех экземплярах магнитной ленты (в, г, д, е) и сместим их друг относительно друга на отрезок, соответствующий периоду повторения Т^*) (этот период мы знаем, так как сами его создавали, посылая зондирующие импульсы). Сложим сигналы со всех четырех лент (перепишем совместно все четыре сдвинутые ленты на пятую). Результат сложения показан на ленте ж.

^*) (Подбор правильного смещения (до совпадения импульсов) равносилен подбору нужного числа оборотов диска, описанному в начале задачи.)

В момент, когда импульс имеется на всех четырех лентах, на пятой мы получим импульс А учетверенной амплитуды (например, 4 В). В моменты, когда импульс имеется только на трех лентах, на пятой получим импульсы Б₁ и Б₂ утроенной амплитуды, и т. д. Помехи записаны на всех лентах, но они случайны, интервалы между ними не равны Т, поэтому при сдвиге лент на Т они не совпали друг с другом (то же было на диске, на кинокадре) и поэтому не сложились (импульсы Д на ленте ж с амплитудой 1 В). Правда, одна из помех ленты в чисто случайно совпала с помехой ленты г и дала на ленте ж импульс Е двойной амплитуды .(то же произошло кое-где и со случайными кружками на диске, см. рис. 65). Вероятность такого совпадения мала. Еще меньше вероятность совпадения помех на трех лентах. И уже совсем маловероятно совпадение на всех лентах (особенно если их много, например двадцать). Таким образом, совпадение на всех четырех лентах свидетельствует с большой уверенностью, что это сигнал.

Отбросим все импульсы, амплитуды которых меньше 4 В, и сохраним остальные (это можно сделать с помощью ограничителя - устройства, пропускающего только сигналы, превосходящие некоторый порог ограничения, например, 3,5 В). Этим самым мы отбросим все помехи и оставим только сигнал А' (лента з). Сравнивая его положение на оси времени с положением последнего зондирующего импульса (4 на ленте а), мы определим запаздывание tR (лента з) и по нему - расстояние.

Разумеется, в радиолокаторе и запись, и считывание ведутся автоматически и непрерывно, результаты выдаются немедленно.

Между прочим, магнитная лента - не лучшее из того, чем располагает радиолокация. Здесь она употреблена только для наглядности.

И последний вопрос: а что, если помеха придет сильная, вчетверо больше сигнала (лента е, импульс К, показанный пунктиром)? Тогда она одна, ни с чем не складываясь, достигнет порога ограничения (К" на ленте ж) и появится на выходе (К" на ленте з). Этот же вопрос применительно к диску: а что, если бы один из случайных кружков на рис. 64 был вшестеро ярче других? Тогда он один при вращении диска дал бы на рис. 65 шесть кружков, по яркости равных сигналу и равномерно расположенных по кругу.

Ответ прост: такой кружок мы заметили бы еще на неподвижном диске и могли бы заретушировать так, чтобы он не выпячивался среди остальных. Этот же ответ применительно к радиолокатору: можно было бы с помощью еще одного ограничителя подравнять амплитуды всех импульсов в, г, д, е еще до сложения. Этим мы лишили бы помеху ее амплитудного преимущества, сохраняя за сигналом преимущество коллектива, против которого одиночная помеха бессильна.