53. Смотри на круги

А В большой круглой миске - вода. Вы роняете в воду плавучии предмет (хлебную крошку и т.п.), стараясь попасть в центр. Как без инструментов проверить, насколько вам это удалось?

Бросая в воду камешки, смотри на круги, 
ими образуемые; иначе такое бросание 
будет пустою забавою.

Козьма Прутков "Мысли и афоризмы", № 156.

Б Проделайте этот эксперимент. Если вы наблюдательны, то Н он вам подскажет способ проверки. Впрочем, исчерпывающей подсказкой является мысль Пруткова. Круги легче наблюдать, когда в зеркале воды отражается что-либо пестрое (листва деревьев, облака и др.). Если отражается чистое небо, то горбы и впадины волн не отличить от наклонных участков, т. е. картина волн наблюдается с большим трудом.

В Нужно наблюдать за отраженной волной. Если крошка упала точно в центр, то возбужденная ею круговая волна достигнет краев миски одновременно во всех точках. Благодаря этому отраженная волна тоже будет круговой и, распространяясь от краев к центру, сфокусируется точно в месте своего возникновения, отмечаемом плавающей крошкой.

Если же крошка не попала в центр, то отраженная волна сфокусируется не в центре, а в точке, находящейся по другую сторону от Центра, симметрично с крошкой. Это позволит вам немедленно уточнить второй бросок: вторую крошку нужно бросить посредине между точками исхода и схождения волн.

Строго говоря, отраженные волны фокусируются в точку только при условии, что вы попали крошкой точно в центр. При любом другом положении источника колебаний фокусировка в круглой миске будет несовершенной: отраженные волны не будут точными кругами и будут сходиться уже не в одной точке, а на некотором отрезке. Это легко заметить, если крошку уронить достаточно далеко от центра. Однако и в этом случае картина волн покажет, в какую сторону и как сильно вы отклонились.

Если бы миска была эллиптической (блюдо), то для получения круговой отраженной волны нужно было бы попасть крошкой в один из фокусов эллипса (рис. 67). Тогда отраженные волны сошлись бы во втором фокусе. Именно таково свойство эллипса: ломаная АСВ, соединяющая фокусы эллипса А и В с любой точкой эллипса С, имеет постоянную длину.

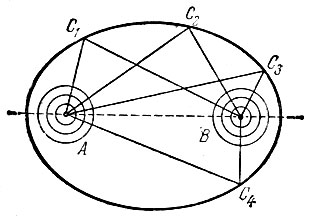
Рис. 67

Если бы сосуд имел параболическую форму (таких не бывает, так как парабола - незамкнутая кривая) и вы бросили бы крошку в фокус параболы, то отраженные волны были бы не кривыми, а прямолинейными (рис. 68), т. е. фокусировались бы в бесконечности. Картина будет тем отчетливее, чем дальше от фокуса экран Э, замыкающий сосуд.

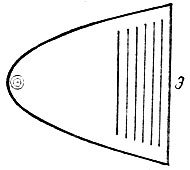
Рис. 68