54. Пловцы и волны

А Перед вами "снимок" глади озера сверху (рис. 69). Точки - пловцы, окружности - волны. Куда плывут пловцы? Какой из пловцов плывет быстрее? Какова скорость пловцов, если скорость волн 0,5 ^м/_с?

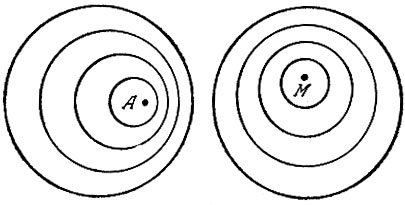
Рис. 69

Отыщи всему начало, и ты 
многое поймешь

Козьма Прутков "Мысли и афоризмы", № 92а.

Б Найдите точки, в которых находились пловцы в начале заплыва. Стоп! Дальше не читать! Подумайте!

Если ничего не придумали, читайте дальше. Скорость волны одинакова по всем направлениям. Поэтому волна и является окружностью: от той точки, где она возникла (центра окружности), она прошла по всем направлениям одинаковое расстояние. Очевидно, самая первая волна успела продвинуться дальше всех. Значит, это окружность наибольшего радиуса. Центр этой окружности и есть место старта пловца. Теперь вы без труда ответите на поставленные вопросы.

В Каждая волна создается пловцом. Очевидно, центры всех окружностей изображают последовательные положения пловца. Центр самой большой окружности О₁ (рис. 70) изображает первоначальное положение пловца. Следовательно, пловец А плывет вправо, пловец М - вперед (на чертеже - вверх). За время, за которое пловец проплыл из точки О₁ в А, волна 1 прошла расстояние О₁B = О₁C = O₁D = О₁E. Расстояние О₁В, как следует из измерений по рисунку, вдвое больше расстояния O₁A. Следовательно, скорость пловца А вдвое меньше скорости волны, т. е. равна 0,25 ^м/_с. Аналогично измеряем скорость пловца М. Она еще меньше - 0,125 ^м/_с.

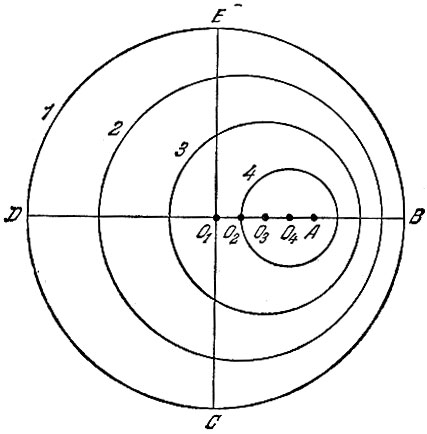
Рис. 70

Оценим теперь качественно картину волн в зависимости от скорости пловца. Если пловец барахтается на месте, он создает концентрические кольца волн. Если он движется, то волны сгущаются в том направлении, куда он плывет, и разрежаются в противоположном направлении. Сгущение тем сильнее, чем больше скорость пловца. Так будет до тех пор, пока скорость пловца не сравняется со скоростью волн. Тогда все окружности - большие и малые - касаются друг друга в "одной точке, а именно в той, в которой находится пловец (рис. 71, а). Если пловец движется быстрее волн, то картина оказывается сложнее (рис. 71, б). Наиболее отчетливо в ней виден клин из двух прямых волн АВ к АС - общих касательных ко всем круговым волнам. Внутри же клина картина очень запутана: здесь в отдельных местах гребень одной волны складывается с гребнем другой и получается более высокий гребень, в других же местах складываются две впадины, в третьих - гребень одной со впадиной другой. И только на прямых АВ и АС мы имеем простую картину: вдоль этих прямых выстроились гребни всех кольцевых волн.

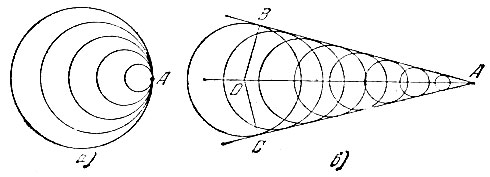
Рис. 71

Построив точку старта О и соединив ее с А и В, мы получаем прямоугольный треугольник ОАВ, у которого гипотенуза ОА изображает путь, пройденный пловцом, а катет ОВ - путь, пройденный волной за то же время t. Если обозначить угол ВАС буквой а, то ^ОВ/_ОА = sin (^α/₂). Разделив числитель и знаменатель левой части на t, мы получаем слева отношение скоростей волны v_B и пловца v_П. Таким образом, скорость пловца можно найти по формуле

Чем острее клин (меньше α), тем больше скорость пловца.

Отметим, что аналогичный клин звуковых волн создается у самолета, летящего со скоростью, большей скорости звуковых волн (со сверхзвуковой скоростью). Этот клин (точнее, поверхность конуса, поскольку в этом случае речь идет о движении волн в среде с тремя измерениями), набегая на наблюдателя, создает у него впечатление орудийного выстрела, после которого наблюдатель, находясь уже внутри конуса, начинает слышать обычный звук самолета.

Такой конус показан на рис. 72 (а - вид сбоку, б - вид сверху). На поверхности конуса давление выше, чем снаружи и внутри. Вблизи самолета перепад давления может достигать значительной величины, зависящей от высоты полета, типа машины, ее скорости; поэтому ударная волна низко летящего сверхзвукового самолета может произвести заметные разрушения. Но при высоте полета более 10 000 м волна достигает земли с давлением, превышающим атмосферное не более чем на доли процента.

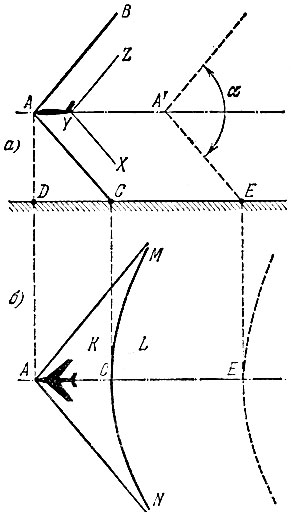
Рис. 72

Земной наблюдатель D видит самолет А в зените, но не слышит его звука; на наблюдателя С в данный момент набегает поверхность конуса с повышенным давлением, и он слышит "выстрел". Наблюдатель Е находится внутри конуса, он слышал "выстрел" в момент, когда самолет находился в точке А', а сейчас слышит обычный гул самолета.

Часто удается различить, что "выстрел" двойной: второй удар происходит от хвостовой волны XYZ (на поверхности этого конуса давление ниже, чем снаружи и внутри).

Линия пересечения конуса и плоской поверхности земли - гипербола NCM, во всех точках которой "выстрел" слышен одновременно. Она отделяет зону К, в которой самолет еще не слышен, от зоны L, в которой он уже слышен. Эта гипербола движется по земле ,со скоростью самолета. Кстати, не поленитесь вычислить эту скорость, исходя из того, что на рисунке α = 100°.

Более подробно об этом явлении можно прочесть в брошюре: Миронов А. Д. Сверхзвуковой "хлопок" самолета.- М.: Воениздат, 1964.

Обратите внимание, что приведенная формула при v_П < v_B дает

что невозможно. Не надо думать, что это ставит под сомнение правильность формулы. Наоборот, своим экстравагантным поведением формула предостерегает читателя, чтобы он держал ухо востро: облаеть применения формулы кончилась, при vu