71. Даешь полумесяц!

А Представим, что лучшей половине человечества из непонятного (но обязательного для исполнения худшей половиной) каприза захотелось, чтобы Луна всегда была не слишком полной и не слишком серпом, а точно полумесяцем. Так сказать, не макси, не мини, а миди! Найдите геометрическое место точек в Солнечной системе, которые удовлетворяют этому капризу. Сумеете ли вы подобрать для Луны соответствующую орбиту?

Б Рассмотрите треугольник Солнце - Земля - Луна. Каким он должен быть, чтобы мы с Земли видели лунный диск освещенным ровно наполовину?

В Рис. 93 напоминает вам о том, как возникают различные фазы Луны. Размеры Луны и ее орбиты на рисунке сильно преувеличены по сравнению с Солнцем, Землей и расстоянием между ними ЗС. Это позволяет детально рассмотреть Луну и ее фазы и, кроме того, не считаться с эффектами параллакса, вызываемыми конечными размерами Солнца и Земли.

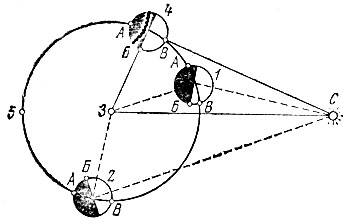
Рис. 93

В положении 1 (угол Земля - Луна - Солнце тупой) Земля видит большую часть Луны А Б неосвещенной и меньшую Б В (серпик) - освещенной. В положении 2 (угол ЗЛС острый) - наоборот. В положении 4 (угол ЗЛС прямой!) АБ = БВ, т. е. мы видим полумесяц. Очевидно, прямой угол у Луны есть обязательное требование для фазы полумесяца.

Будем для простоты расстояние Земля - Солнце (ЗС) считать постоянным и прямую ЗС неподвижной. Найти геометрическое место вершин прямого угла, опирающегося на отрезок ЗС, легко: вспомним, что если вершина угла, опирающегося на диаметр, лежит на окружности, то этот угол -прямой. Значит, геометрическим местом положений Луны, дающих полумесяц, является окружность, построенная на отрезке ЗС как на диаметре (рис. 94). Переходя от плоского чертежа к трехмерному космосу, мы в качестве искомого геометрического места будем иметь шаровую поверхность, построенную на том же диаметре.

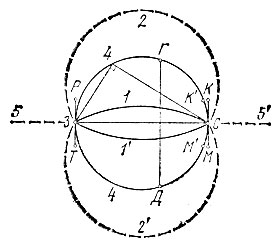
Рис. 94

Геометрическое место точек для серпика (положение 1 на рис. 93) также находится на дуге окружности (1 на рис. 94), только большего радиуса, так как теперь отрезок ЗС должен быть хордой (искомый угол - тупой, а не прямой).

Любопытно, однако, что на продолжении дуги 1 (по другую сторону от точек 3 и С) будет не светлый, а темный серпик тех же размеров (фазы), т. е. светлая, часть Луны будет не серпиком, а его дополнением до полной Луны. Если же требуется светлый серпик, то нужно построить дугу 1' того же радиуса, что и 1, но принадлежащую другой окружности. Итак, геометрическим местом серповидной Луны на плоскости является не окружность 1, а сочетание дуг 1 и 1'. В пространстве геометрическим местом будет поверхность типа веретена, образованная вращением дуги 1 вокруг прямой ЗС. Аналогично, черный серпик (ущербленная Луна) получается вращением дуги 2 вокруг той же прямой (при этом полученная поверхность напоминает поверхность яблока). Для полной Луны геометрическим местом точек являются две полупрямые: З5 и С5' (однако на первой из них Луна находится в тени Земли, на второй - , спрятана от нас за Солнцем); для новолуния - отрезок ЗС.

С геометрией покончено. Перейдем к физике (небесной механике). Задачу можно решить, остановив Луну (относительно Земли) в положении 4 (рис. 94). Но тогда она упадет на Землю. Добровольно по окружности 4 Луна не пойдет: траектория 4 явно не кеплеро-ва (как и "веретено", и "яблоко"). Кроме того, даже если мы принудим ее к этому с помощью двигателей, то она после полуоборота все равно столкнется либо с Солнцем, либо с Землей.

Но нам вовсе не обязательно держать Луну в плоскости чертежа. Ведь геометрическим местом точек для полумесяца является сфера 4. Если бы Луна двигалась по окружности, перпендикулярной прямой ЗС (например, в плоскости ГД), то фаза ее была бы постоянной (полумесяц - на сфере 4, серп - на веретене 1 и т.д.). Но эта траектория тоже не кеплерова: у кеплеровой центр притяжения (либо Солнце, либо Земля) должен находиться в плоскости орбиты. Задание будет "почти выполнено", если Луну заставить вращаться вокруг Солнца в плоскости КМ. Поскольку точки К и М мало отличаются от нужных К' и М', то и фаза Луны будет мало отличаться от полумесяца. Авось заказчик не заметит разницы! Тем более, что теперь Луна будет видна с Земли лишь как очень яркая точка, а проверить правильность выполнения задания можно только через телескоп. Кроме трудностей перевода Луны на эту орбиту здесь есть и другие: плоскость должна быть всегда перпендикулярна прямой ЗС, которая, как известно, поворачивается. Итак, придется еще заставить плоскость КМ совершать один оборот в год вокруг оси КМ.

После всех этих фантастических трудностей орбита в плоскости РТ (содержащей Землю) кажется почти реальной (хотя плоскость РТ тоже нужно поворачивать, как и КМ). Еще ближе к реализуемости проект, в котором используется не сама Луна, а ее эрзац, созданный искусственно. Выведем на орбиту в плоскость РТ диск (диаметром 90 км, расстояние от Земли 10 тыс. км). Пристроим перпендикулярно диску гантель (см. задачу 35) длиной порядка 1000 км, тогда диск все время будет смотреть на Землю, и будет неотличим от шара (впрочем, можно сделать и надувной шар). Зачерним половину диска (шара), а вторую сделаем люминесцирующей или прозрачной, тогда внутрь можно поместить источники света (питаемые от солнечной батареи, роль которой, возможно, удастся поручить зачерненной половине). Заказ исполнен. Правда, с помощью поддельной Луны.