73. Двухпозиционная локация

А На сколько нужно^ отодвинуть Луну, чтобы она оказалась на пределе видимости невооруженным глазом?

Б Задача кажется повторением предыдущей. С расстояния 29 м мяч, освещенный полностью солнечным светом, имеет такую же звездную величину (-12,7), как и полная Луна. Увеличивая расстояние до мяча в 5500 раз (см. предыдущую задачу), т. е. до 160 км, мы превратили его в объект 6-й звездной величины, находящийся на пределе видимости. То же надо сделать и с Луной! Увеличивая расстояние до Луны в 5500 раз, мы получаем решение задачи. Новое расстояние до Луны

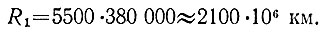
Эта величина, полученная по аналогии с предыдущей задачей, не вызывает у вас сомнений, пока вы не представите, где при этом окажется Луна. А она окажется между Сатурном (1426*10⁶ км от Солнца) и Ураном (2869*10⁶ км). Сравним Луну с Ураном. Диаметр Урана в 10,3 раза больше диаметра Луны (главное сечение - в 10,3² ≈ 10⁶ раз), а его альбедо (0,66) - в 10 раз. Следовательно, отодвинутая Луна будет слабее Урана в

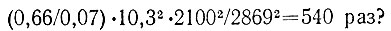
Но видимая звездная величина Урана равна + 5,7, т. е. он уже находится практически на пределе видимости. А Луна - в 540 раз слабее! Это противоречит нашему решению: ведь мы ее отодвигали именно на предел видимости.

Аналогичная невязка результатов получается, если сравнивать отодвинутую Луну со спутниками Юпитера. Для Юпитера и его спутников расстояние от Солнца R₂ = 778*10⁶ км, т. е. расстояние от земного наблюдателя, соответствующее полной фазе Юпитера и спутников (противостояние), равно

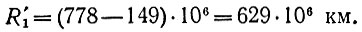
Первый спутник Юпитера Ио по размерам совпадает с Луной (d_Иo = 3460 км, d_Л = 3476 км), по альбедо (0,57) превосходит ее в 8 раз. Видимая звездная величина в противостоянии равна + 5, т. е. лишь в 2,5 раза лучше предела видимости. Значит, Луна, отодвинутая на 2100*10⁶ км, будет видна слабее в

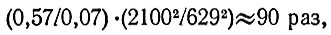
т. е. находится далеко за пределами видимости.

Мы опять получили большую ошибку в ту же сторону, в сторону ослабления видимости Луны по сравнению с заданной. Эти невязки результатов означают одно из двух: либо астрономы неправильно рассчитали всю Солнечную систему, либо данная задача вовсе не является повторением предыдущей. А то, что различные проверки (по Урану и Ио - объектам, находящимся на разных дальностях) дают существенно разную величину ошибки (в 90 и 540 раз), означает, что зависимость видимости объекта от дальности в этой задаче является существенно иной, чем в предыдущей. В частности, рост ошибки с расстоянием означает, что эта зависимость более сильная, чем обратная пропорциональность квадрату расстояния.

В В предыдущей задаче расстояния Земля - мяч (29 м и 160 км) и Земля - Луна были пренебрежимо малыми по сравнению с расстоянием Земля - Солнце. Здесь же расстояние Земля - Луна (отодвинутая) существенно больше расстояния Земля - Солнце. Это придает совершенно иной характер задаче: ведь Солнце - источник света для мяча и Луны, и расстояние него небезразлично для освещенности и видимости этих объектов.

Отодвигая мяч вдвое дальше, мы могли с полным основанием утверждать, что освещенность его не меняется, а поэтому количество света, попадающего от мяча в глаз, уменьшается вчетвероз принимаемая мощность обратно пропорциональна квадрату расстояния от источника света (мяча):

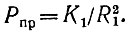
(1)

Отодвигая Луну на миллионы километров (рис. 95), мы должны уже учитывать, что мы ее отодвигаем не только от Земли (R₁), но и от Солнца (R₂), отчего отражаемая мощность

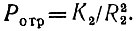
(2)

Рис. 95

Мы не будем детально расшифровывать смысл коэффициентов пропорциональности К₁ и К₂, отметим только, что Р_пр пропорционально Р_отр, т. е. Ротр содержится неявно в коэффициенте K₁

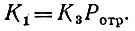
(3)

Тогда

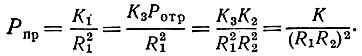
(4)

Эта формула очень любопытна: принимаемая наблюдателем мощность обратно пропорциональна квадрату произведения обоих расстояний.

Чтобы решить задачу, полезно несколько преобразовать формулу (4). Будем интересоваться полной (или почти полной) Луной, для чего, как известно из предыдущих задач, нужно, чтобы на рис. 95 угол γ → 0). Тогда в формуле (4) можно одну переменную (R2) просто выразить через другую (R₁):

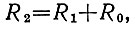
(5)

и, следовательно,

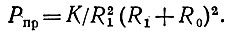
(6)

Для Луны в ее законном положении

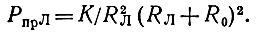
(7)

Тогда

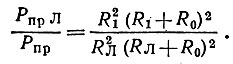
(8)

С учетом предыдущей задачи ^{Р_{пр Л}}/_Рпр = 2,5^18,7 = 3*10⁷. Знаменатель формулы (8) известен:

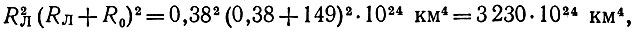
поэтому требуемая величина

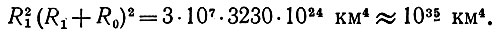
(9)

Мы получили уравнение четвертой степени

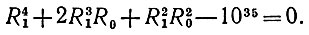
(10)

Его точное решение крайне громоздко и не в духе нашей книги: поскольку оно уже есть в справочниках, то нас оно не интересует. Поэтому мы ограничимся простым подбором. При R₀ << R₁ формула (9) упрощается: R₁⁴ ≈10³⁵ км⁴, что дает R₁ ≈ 5,6*10⁸ км. Поскольку это R₁ все-таки не так уж сильно превосходит R₀, то настоящее R₁ будет несколько меньше. Беря наугад R₁ = 5*10⁸ км, получаем по точной формуле (9)

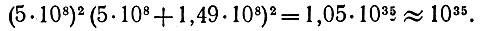
Итак, Луну нужно отодвинуть от Земли приблизительно на R₁ = 500*10⁶ км (примерно на средину между Марсом и Юпитером). Имеют ли полученные результаты (главный из них - формула (4)) какое-либо практическое значение? Казалось бы, нет: ведь ни автор, ни читатели не собираются всерьез передвигать куда-либо Луну, тем более с такой ограниченной целью. Однако представьте себе какое-либо небесное тело, обращающееся вокруг Солнца по очень вытянутой эллиптической орбите. Такие тела в Солнечной системе есть: малые планеты - астероиды (Гидальго, Икар и др.). У астероида Адонис, например, перигелий находится вблизи орбиты Меркурия, а афелий- вблизи орбиты Юпитера. Ясно, что формула (4) необходима для вычисления их видимости (с поправкой на фазу планеты). И вообще формула (4) описывает наблюдаемость любого

отражателя для случая, когда источник излучения (Солнце, передатчик и др.) и наблюдатель отраженного сигнала (Земля, приемник и др.) находятся в разных точках (занимают разные позиции). Например, формула (4) описывает условия обнаружения отражающей цели (самолета и др.) в двухпози-ционной радиолокации.

Преобразуем формулу (4) к каноническому виду. Пусты в сиcтеме декартовых координат (х, у) на осих симметрично относительно нуля расположены передатчик F₁ и приемник F₂ (рис. 96). Найдем геометрическое место точек отражателя Л1, для которых его наблюдаемость приемником F2 постоянна. Очевидно, это множество точек, для которых ¹/_R1²R2² = const или, что то же самое,

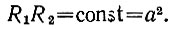
(11)

Обозначим F₁O = OF₂ = c и выразим R₁ и R₂ через с, х и у. Из рис. 96 видно, что

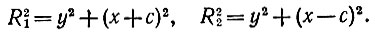
(12)

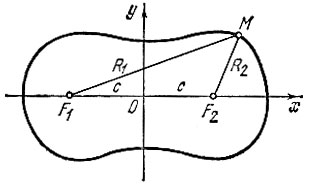
Рис. 96

Тогда R₁²R₂² = a⁴ = [y² + (x + c)²]*[y² + (x - с)²], и после элементарных преобразований получаем

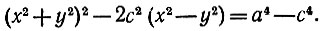
(13)

Это есть уравнение овала Кассини - геометрического места точек M, для которых произведение расстояний R₁ и R₂ от двух фокусов F₁ и F₂ есть величина постоянная. Полезно сравнить с определением эллипса - геометрического места точек, для которых сумма расстояний R₁ и R₂ от двух фокусов F¹ и F₂ есть величина постоянная.

Форма овала Кассини весьма причудливо зависит от отношения между с и 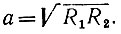. При а > √2 овалы имеют эллипсовидную форму (овалы 1 и 2 на рис. 97); при с < а < a√2 овал имеет два утолщения (кривые 3 № 4); при а = с кривая приобретает вид "восьмерки" (кривая 5, этот частный случай овала Кассини называется лемнискатой Бернулли); при а <2 с овал распадается на два яйцевидных овала (кривые 6 и 7). Предельными слулаями овалов Кассини являются окружности. При а → ∞ имеем окружность бесконечно большого радиуса R₁ = R₂ = R = a. Формально этот результат получается из уравнения (13), которое при c → 0 превращается в уравнение окружности радиуса а с центром в начале координат х² + у² = а². Случай а → ∞ при c = const геометрически подобен случаю с → 0 при а = const. Физически это означает, что при а >> с можно пренебречь расстоянием между двумя позициями F₁ и F₂ и считать радиолокатор однопозиционным, для которого ¹/_R1²R2² = ¹/_R⁴. При c → 0 два частных овала стягиваются к двум бесконечно малым окружностям, охватывающим точки F₁ и F₂ (все манипуляции с мячом в предыдущей задаче мы проделывали в очень малой окрестности точки F₂).

Для радиолокации (светолокации - астрономии, звуколокации и др.) овалы Кассини имеют следующий смысл. От цели, находящейся в любой точке на данном овале, в фокусе будет принята одна и та же мощность (если передатчик, облучающий цель, находится во втором фокусе). Если эта мощность находится на пределе чувствительности, то данный овал охватывает собой зону действия радиолокатора. В трехмерном пространстве это поверхность, образованная вращением овала вокруг оси х. Мощность принятого сигнала тем выше, чем больше номер овала Кассини, на котором находится цель (если нумеровать, как на рис. 97).

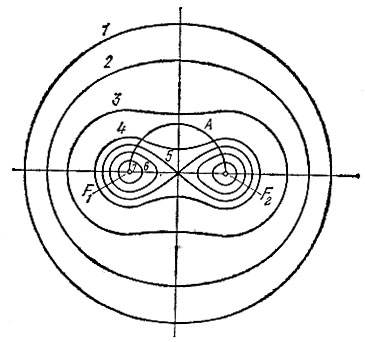
Рис. 97

На рис. 97 кривая F₁AF₂ - полуокружность, построенная на отрезке F₁F₂ как на диаметре. Если вспомнить задачу 71, то это есть геометрическое место точек, в которых Луна имеет фазу полумесяца. Кривая А удобна для нашего анализа, так как позволяет не беспокоиться о постоянстве фазы. Видно, что вблизи точек F₁ и F₂ кривая А пересекает овалы с высоким номером, а посредине - с малым. Это означает, что Луна будет давать на Земле одинаково интенсивный свет в двух положениях: F₂ рядом с Землей и F₁ рядом с Солнцем, хотя угловые размеры ее при наблюдении с Земли велики в первом случае и ничтожно малы во втором. Правда, чтобы, находясь рядом с F₁, освещать Землю так, как она освещает ее на своем законном месте, Луна должна находиться уже внутри Солнца (радиус Солнца больше расстояния Земля - Луна).

Впрочем, формула (4) выведена в предположении точечного источника света и поэтому в непосредственной близости от реального Солнца дает некоторую погрешность.

Если Луна находится на середине дуги F₁AF₂, то сигнал от нее довольно мал (меньше, чем от Меркурия).

Аналогично ведет себя и сигнал, отраженный от самолета. Так, например, описанная в конце задачи 61 помеха от самолета телевидению проявляется сильно, когда самолет пролетает в непосредственной близости или от приемной антенны телевизора, или от передающей антенны телецентра. Самолет почти не дает помехи, когда пролетает на полпути между телевизором и телецентром. Зона действия мешающего самолета для вашего телевизора, таким образом, распадается на два яйцевидных овала, один из которых охватывает телецентр, а второй - ваш телевизор.