89. Лицом к лицу с точностью

А В этой задаче вам предстоит проверить себя на вполне серьезной научной работе. Допустим, что вы взялись за постановку того опыта, который описан в конце предыдущей задачи. Длина каждого зеркала 100 м, требуется получить около 1000 отражений. Вам нужно установить зеркало на европейском берегу Гибралтара строго параллельно зеркалу африканского берега. Мобилизовав все свое умение, вы установили его так, что непараллельность зеркал, если она и есть, составляет не более 0,0001°. Не правда ли, такой точностью можно гордиться!

Устроит ли вас эта точность? Какие другие трудности вам удастся предвидеть?

Б Обычно на вопрос о точности отвечают так. Мы знаем, что если зеркало повернуть на угол γ, то отраженный луч повернется на 2γ. Это легко доказать.

Если зеркало CD (рис. 131) параллельно зеркалу АВ, то все углы падения и углы отражения одинаковы и равны α. Если зеркало CD повернуть на угол γ (в положение CD'), то угол падения на него в точке F уменьшится на угол γ (потому что перпендикуляр FE повернется на угол γ, в положение FE'). Но если угол падения KFE' стал равен α - γ, то угол отражения E'FL тоже будет α - γ, отчего угол EFL станет α - 2γ. Таков будет угол падения в точке L.

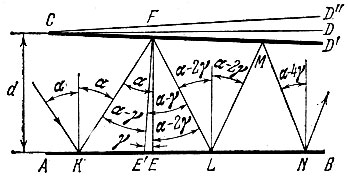
Рис. 131

Итак, после отражений в К и F луч повернулся на 2γ, в L и М - еще на 2γ, и т. д. После тысячи отражений он повернется на 1OOOγ относительно того направления, под которым он вышел бы из системы зеркал, если бы оба зеркала были строго параллельны.

В нашем случае 1000γ = 0,1°. Этот угол настолько мал, что не повлияет заметно на длины отрезков KF, FL, LM и т. д. Эти длины по-прежнему можно будет считать равными d. Следовательно, такая точность нас устраивает. Просто приемник света придется немного передвинуть вправо или влево.

Рассуждения, в общем, правильные, но останавливаться рано. Внимательно учтя все обстоятельства, мы обнаружим, что из-за столь ничтожной погрешности луч вообще не появится на выходе системы зеркал (т. е. справа), а вернется обратно налево. Напомним, что мы еще не использовали длину зеркал, а также ширину Гибралтара Rt которая равна 14 км.

От малых причин бывают великие последствия; 
так, отгрызение заусенца причинило моему 
знакомому рак.

Козьма Прутков "Мысли и афоризмы", № 79а.

В Рассчитаем первоначальный угол падения α. Не зная точного значения и знака погрешности установки γ (если бы мы знали, то могли бы устранить; мы знаем только, что она не больше 0,0001°), расчет будем вести, исходя из гипотезы, что погрешности нет. На стометровой системе зеркал 1000 отражений расположатся через 10 см. При расстоянии между зеркалами 14 000 м угол а будет

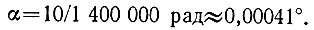
Если погрешность равна 0,0001°, то после каждого отражения из угла падения будет вычитаться 0,0001°. В результате после пятого отражения угол падения будет

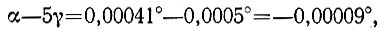
т. е. будет уже отрицательным, а это значит, что луч, перестав передвигаться в системе зеркал вправо, повернет влево. Двигаясь влево, он совершит еще 4-5 отражений и выйдет из системы зеркал. Таким образом, всего будет около десятка отражений вместо требуемой тысячи. Система зеркал как бы выталкивает луч обратно (рис. 132). Чем меньше погрешность 7, тем глубже проникнет в систему луч.

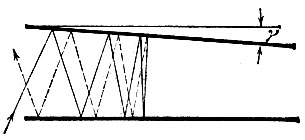
Рис. 132

Если знак погрешности противоположный (CD" на рис. 131), то луч пройдет всю систему зеркал, но теперь после каждого отражения угол падения будет возрастать на γ, отчего луч пробежит на выход слишком быстро, число отражений будет опять недостаточным.

Это явление можно использовать для других целей: для измерения очень малых углов. Система почти параллельных зеркал работает как усилитель угла поворота. Пока зеркала строго параллельны, луч выходит из системы под тем же углом, под которым .он вошел в нее, независимо от числа отражений n. Стоит, однако, повернуть одно из зеркал на ничтожно малый угол γ, как выходной луч повернется на угол nγ, который мы можем измерить в n раз точнее (при той же абсолютной погрешности), чем непосредственно угол γ. Мы получаем своеобразный "угловой микроскоп", увеличивающий, в отличие от обычного микроскопа, не линейные размеры, а углы. Правда, для того чтобы этот "микроскоп" был точным, зеркала должны быть идеально плоскими (иначе угол γ будет перехменным вдоль зеркала и вместо nγ мы будем иметь γ₁ + γ₂ + γ₃ + ... + γ_n).

Однако мы отвлеклись от нашей задачи. Как же все-таки получить тысячу отражений? В предыдущем примере луч повернул обратно после пятого отражения, потому что угол α = 0,00041° был полностью исчерпан за пять шагов с помощью угла γ = 0,0001°. А если взять а=0,1°=1000т? Тогда этот угол будет исчерпан (и луч повернет обратно) только после 1000 отражений! Или взять α = 0,05°? Тогда луч повернет назад после 500 отражений и, претерпев на обратном пути еще 500, выйдет из системы там же, где вошел, имея на своем трудовом счету 1000 отражений.

Рассуждения интересные, однако они не учитывают конечной длины зеркал. Подсчитаем, какое максимальное число отражений возможно в нашей системе. Максимум будет, очевидно, тогда, когда будет использована вся длина зеркала, причем "гармошка" луча будет наиболее сжатой. Надо послать слева в систему луч под таким углом, чтобы он вышел справа как раз в тот момент, когда он уже готов повернуть обратно, т. е. когда он перпендикулярен к зеркалу АВ (рис. 133). Удобнее, однако, решать задачу с конца, рассматривая ход луча справа налево. Это, очевидно, одно и то же, так как если луч повернуть на 180°, то он в точности повторит путь между зеркалами в обратном порядке.

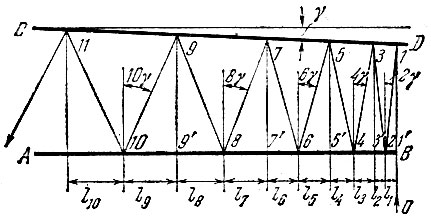
Рис. 133

Итак, введем в систему справа луч 01, перпендикулярный к зеркалу АВ и падающий на зеркало CD под углом γ = 0,0001^о (педантичный читатель найдет, что еще лучше было бы луч 01 слегка наклонить вправо, на угол чуть-чуть меньше γ, однако мы не будем мелочны, так как от этого число отражений в лучшем случае возрастет только на единицу). Найдем расположение точек 1', 2, 3', 4, 5'9 . . . вдоль зеркала АВ (1', 3', 5',. . . - проекции точек 1, 3, 5, ... на зеркало АВ). Приняв точку 1' за начало отсчета, имеем

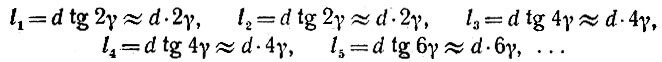
Крайняя правая часть формул представляет собой естественное упрощение, так как при столь малом γ с высокой степенью точности tg γ = γ и даже tg 1000γ ≅ 1000γ (здесь γ в радианах).- Предполагается, что расстояние между зеркалами везде равно d, несмотря на их непараллельность. При большом d (Гибралтар!) и столь малой непараллельности такое предположение допустимо.

Будем складывать l₁, l₂, l₃, . . ., пока их сумма не сравняется при некотором l_i с длиной зеркала L = 100 м (очевидно, i будет номером последнего отражения, т. е. максимальным возможным числом отражений; на рис. 133 i = 11):

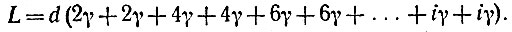
Отделяя от каждого нечетного слагаемого по одному γ, т. е. отделив всего ^iγ/₂, мы получаем арифметическую прогрессию (плюс ^iγ/₂):

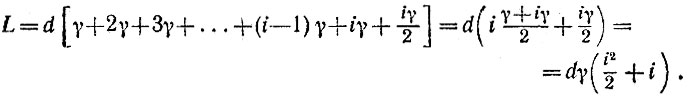
При большом i вторым слагаемым можно пренебречь по сравнению с первым, и тогда

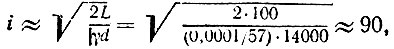
что намного меньше нужной нам тысячи.

Угол α, под которым луч выходит из системы,

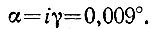
Используя ход луча туда и обратно, число отражений можно удвоить (180), но и этого нам мало.

Итак, та фантастически высокая точность, которую каким-то чудом вы получили при установке зеркал, оказывается недостаточной. Особенно ощутимой станет нехватка точности, если вам выдадут вместо стометровых зеркал метровые.

К счастью, есть способ повысить точность. Он опирается не на измерение угла γ, а на непосредственный подсчет числа полученных отражений. Представьте, что лазер посылает в систему непараллельных зеркал короткий световой импульс (длительностью в 1 мкс, например). Отразившись неизвестное число раз, импульс возвращается. Число отражений можно определить ло времени запаздывания отраженного импульса по отношению к посланному (радиолокация или, точнее, светолокация). Свет проходит в секунду 300 000 км. Если отраженный импульс запоздает, например, на 0,0007 с, то это значит, что он прошел 210 км, т. е. пересек Гибралтар 15 раз. Осторожно доворачивая зеркало и следя за возрастающим запаздыванием сигнала, мы можем добиться нужного нам числа отражений.

Чтобы вы не думали, что теперь уже поставить эксперимент Ничего не стоит, перечислим хотя бы часть еще не решенных проблем.

1. До сих пор предполагались идеально плоские зеркала. Но идеального ничего нет. Как исправлять искривления? Может, быть, следя за густотой расположения отражений вдоль зеркала и надавливая легонько в нужных местах на обратную сторону зеркала?
2. Наше стометровое зеркало обладает огромной парусностью. Ветер будет его прогибать (и этим портить всю картину), а может и вообще унести. Нужен штиль.
3. Прозрачность атмосферы должна быть такова, чтобы на пути в 14 км поглощалось намного меньше (например 0,1%), чем при одиночном отражении (6% в предыдущей задаче), иначе это сильно ограничит число отражений. Бывает ли такое состояние атмосферы в Гибралтаре?
4. Если в начале пути луча на зеркале окажется пылинка П₁ от которой свет рассеивается в разные стороны (рис. 134), то часть отраженного ею света попадет на выход напрямик (по пути П₁П₂). А это может обернуться катастрофой для всей идеи измерения скорости расширения Гибралтара. В самом деле, если после 100 отражений от сигнала остается 0,002, то после 1000 - только 0,00210¹⁰ ≈ 10^-27. Если от пылинки П₁ напрямик на пылинку П₂, находящуюся в воздухе, придет хотя бы одна миллиардная часть энергии, поступившей по прямой 2П₁ и от пылинки П₂ в сторону приемника В отразится одна миллиардная от этой миллиардной, то это будет все-таки 10^-18, т. е. в миллиард раз больше, чем полезный сигнал, претерпевший нужные нам 1000 отражений. Мы можем ошибочно принять этот паразитный сигнал за полезный. Однако его доплеровский сдвиг имеет слабую связь с перемещением континентов: до пылинки было только два полезных отражения. Если пылинка (или телеграфный столб) П₂ неподвижна, то эффект Доплера (и измеренная скорость) будет в сотни раз меньше того, который есть в тысячекратно отраженном луче. А если пылинка П₂ сама движется, то, поскольку ее скорость наверняка в десятки тысяч раз выше скорости разбегания континентов, результаты измерений могут оказаться самыми неожиданными. Можно предложить два способа решения проблемы пыли. Первый - перед началом эксперимента обильно полить Африку и Европу из шланга. Второй - поставить между зеркалами экран MN (пунктир на рис. 134), задерживающий рассеянный свет и не мешающий прохождению ломаного отраженного луча. Положение экрана в идеальной системе легко рассчитать, в реальной системе его нужно подбирать экспериментально и регулировать на протяжении всего эксперимента. Если вспомнить, что длина экрана более 10 км, то трудно решить, какой из двух способов проще. Видимо, проще все-таки третий, который предложат читатели^*) .
   
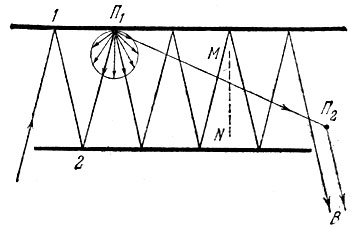
   Рис. 134
   
   
5. До сих пор мы рассматривали идеальный бесконечно тонкий луч. На практике всякий "луч" представляет собой пучок света конечной толщины, причем по мере удаления от источника он, пройдя все фокусирующие устройства, в конце концов неизбежно расширяется^**). Может оказаться, что, начиная с некоторого номера отражения, соседние пятна света на зеркале начнут перекрываться. В результате в приемник поступит не чистый сигнал от последнего отражения, а смесь нескольких соседних отражений, имеющих разные доплеровские сдвиги. К счастью, лазер дает очень тонкий луч света, а с помощью специальной оптики его можно сделать еще тоньше.
6. Проблема постоянства (стабильности) частоты излучения лазера. Допустим, что Европа и Африка взаимно неподвижны, но частота лазера медленно меняется (причем об этом мы не знаем). Тогда к моменту, когда световой сигнал с частотой f₁ пробежав между зеркалами, придет в точку приема, туда же напрямик от лазера поступит сигнал с уже изменившейся частотой f₂ = f₁ + Δf. Смешав эти два колебания (для выделения разностной частоты), мы получим f₂ - f₁ = Δf. Не зная, что частота лазера меняется, мы примем эту разностную частоту за доплеровскую, т. е. сделаем ложный вывод, что континенты движутся. Очевидно, чтобы эксперимент был успешным, нужно, чтобы паразитный уход частоты Δf за время пробега луча был значительно меньше ожидаемого доплеровского сдвига. Ожидается, что континенты расходятся со скоростью
   
   
   При 999 отражениях скорость удлинения полного пути луча будет 1000v = 1 ^мкм/_с, что при λ = 0,5 мкм дает сдвиг частоты на
   
   
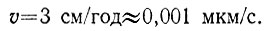   Время пробега луча
   
   
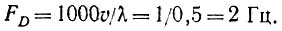   За это время частота лазера (если мы хотим хотя бы обнаружить движение) не имеет права уйти более чем на 2 Гц, т. е. за секунду - не более 40 Гц. А если мы хотим не только обнаружить, но и измерить F_D, хотя бы с точностью до 1%, то уход частоты должен быть еще в 100 раз меньше. Такая стабильность лазеров еще не достигнута: не так-то просто выдерживать с точностью до долей герца невообразимо высокую частоту лазера 6*10¹⁴ Гц!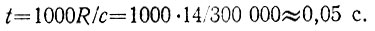
7. Проблема землетрясения. Не того землетрясения, от которого рушатся стены, а того, которое вызывается проезжающим за 100 км от зеркала мотоциклистом или набегающими на берег волнами (колебания зеркал на тысячную долю микрометра в секунду)^***).
8. Десятки других проблем, которые возникнут, как только этим экспериментом займутся вплотную.

^*) (Поскольку предложений от читателей не поступило, придется придумывать самому. Например, почему бы не попробовать просто отодвинуть приемник (точку В) подальше по стрелке? При этом величина сигнала, принимаемого от пылинки П₂, меняется обратно пропорционально квадрату расстояния ВП₂, а величина полезного сигнала - обратно пропорционально квадрату полного пути луча от лазера до В (по ломаной). Отодвигая, например, приемник на 100 км, мы увеличиваем расстояние ВП₂ в тысячи раз и ослабляем помеху в миллионы раз; в то же время расстояние по ломаной, измеряемое тысячами километров, практически не меняется, и поэтому полезный сигнал из-за лишних 100 км почти не ослабевает. Вспомните задачу "Двухпозиционная локация", в которой мы отодвигали Луну, и сравните Луну с пылинкой.)

^**) (Многие читатели уверены, что луч лазера бесконечно тонкий и с увеличением расстояния не расширяется. Но тогда мы могли бы с Земли лучом лазера прожечь насквозь Луну и даже несчастных андромедян. Не слушайте, дети, тех Дядей, которые любят сравнивать реальный лазер с фантастическим гиперболоидом инженера Гарина. )

^***) (Разработаны интерферометры (лазер плюс система зеркал), способные обнаруживать малейшие колебания и приливные волны в земном шаре (см., например: Зарубежная радиоэлектроника, 1976, № 8, с. 107). )