3. Вращение

В предыдущих главах мы разобрали вопрос о несущественности скорости. Однако, если говорить о всех возможных видах движения обычного твердого тела, то поступательная скорость будет лишь одной из характеристик. Ведь кроме поступательного движения такое тело может еще и вращаться. На первый взгляд может показаться, что у вращательного движения, как и поступательного, тоже нет никакого выделенного состояния (вспомним относительность состояния покоя). Но это не так. Мы отлично знаем, что существует такое состояние без вращения, когда тело не испытывает внутренних напряжений, тогда как приведенное во вращение тело подвергается растяжению, и в нем возникают силы, которые не дают его частям, удаленным от оси вращения, разлететься в стороны. В причинах этого нетрудно разобраться. Сила будет отсутствовать лишь в том случае, если движение происходит с постоянной скоростью (как по величине, так и по направлению). Если же тело вращается, то его частицы все время изменяют направление своей скорости. Поэтому должна существовать какая-то сила, удерживающая эти частицы, - центростремительная сила, которая уравновешивает фиктивную центробежную силу, отбрасывающую частицы в стороны. Центростремительная сила обращается в нуль лишь при полном отсутствии вращения. Значит, тот самый закон, из которого следует отсутствие привилегированного состояния покоя в поступательном движении, требует, чтобы во вращательном движении состояние покоя было выделено. Когда мы говорим, что скорость тела равна нулю, мы просто выделяем какое-то состояние покоя. Напротив, говоря, что тело не вращается, мы имеем в виду нечто совершенно определенное, абсолютное.

Скорость вращения тела мы можем определить либо через время его полного оборота, либо через какую-то часть этого времени. Можно, например, говорить о времени, за которое тело поворачивается на 1° или, как это обычно делают математики, на угол, немного превышающий 57° (точнее, 180°, деленные на число π); этот угол называется радианом. Величина, обратная этому времени, называется угловой скоростью. Чем больше угловая скорость, тем быстрее вращается тело. В технике принято говорить о числе оборотов в минуту - в этих единицах обычно измеряется скорость вращения моторов. Во всяком случае, независимо от способа ее измерения, угловая скорость является правильной мерой вращательного движения.

Вращение Земли

Земля является тем телом, вращение которого для нас особенно важно. Как узнать, что Земля вращается? Наверное, самым известным способом является метод маятника Фуко. Чтобы разобрать принцип его действия, представим себе обычный маятник, свободно подвешенный на Северном полюсе и качающийся там. Итак, маятник свободно качается под действием гравитации (силы тяжести), и если мы с самого начала пустили его вычерчивать прямую линию, то он будет продолжать делать это и в дальнейшем. Вращение Земли к этому никакого отношения не имеет, она будет просто вращаться под маятником. Значит, с точки зрения наблюдателя, движущегося вместе с Землей, плоскость колебаний маятника должна будет поворачиваться в направлении, как раз противоположном направлению вращения Земли. Если этот маятник подвесить не на полюсе, а в каком-то другом месте, то положение несколько изменится - вращение Земли будет частично отражаться на плоскости качаний маятника, а частично будет стремиться отклонить маятник от вертикали. Легко видеть, что если взглянуть сверху вниз на Северном полюсе, то покажется, что плоскость колебаний маятника Фуко поворачивается по часовой стрелке; если же взглянуть сверху вниз на Южном полюсе на подвешенный там маятник Фуко, то плоскость его колебаний будет поворачиваться против часовой стрелки. Не требуется особой математической подготовки, чтобы сообразить, что в любом месте между этими точками поверхности Земли положение будет промежуточным. Так, на экваторе плоскость колебаний маятника относительно Земли вообще не будет изменяться, в северных широтах она будет поворачиваться по часовой стрелке, но медленнее, чем на самом полюсе, причем скорость этого вращения при переходе в более низкие широты будет постепенно падать до нуля. В южном полушарии все будет в точности наоборот. Таким образом, маятник Фуко пригоден для обнаружения и измерения вращения Земли вокруг ее оси.

Вращение Земли можно обнаружить и другим путем, а именно - взглянув на "неподвижные" звезды. Земля вращается и по отношению к ним, так что нам кажется, что небесная сфера поворачивается вокруг Земли. Весьма примечателен тот факт, что скорость вращения Земли относительно маятника Фуко, помещенного на полюсе, со всей достижимой для измерения точностью соответствует вращению Земли относительно неподвижных звезд. Поэтому напрашивается вопрос, впервые заданный епископом Беркли в XVIII в. и уточненный затем Э. Махом в конце прошлого столетия, а также Эйнштейном в начале нашего века: как связаны между собой эти две скорости вращения? Грубо говоря, получается, будто дальние объекты вселенной определяют, какое из состояний вращения вблизи нас следует считать истинным вращением, а какое - покоем. Самые точные определения того состояния, в котором вращение отсутствует, проделанные исходя из наблюдений за движениями планет солнечной системы, оказываются в точном согласии с выводами, полученными по наблюдениям удаленных тел. Каким именно образом эти далекие тела определяют состояние отсутствия вращения, не совсем ясно, хотя общая теория относительности Эйнштейна и продвинулась довольно далеко в понимании этого загадочного факта.

Эффект Кориолиса

Казалось бы, динамические эффекты, вызванные вращением Земли, едва ли могут существенно сказываться на нашей повседневной жизни, хотя само вращение довольно просто заметить по звездам, поведению маятника Фуко или гироскопу. Однако приходится признать, что весь строй нашей жизни определяется этим вращением. Оно действует в первую очередь на движение атмосферы, т. е. на ветры. Пожалуй, это влияние проще всего проиллюстрировать на примере патефонного диска (рис. 3). Возьмем шарик и осторожно пустим его в сторону оси этого диска. Если он первоначально покоился относительно диска, то в новом месте он сохранит прежнюю скорость движения вместе с диском, а так как прежде он отстоял от оси на большее расстояние, то будет казаться, что он станет опережать свое новое окру-жение в его вращении. Подобным же образом частица, движущаяся относительно диска по окружности с центром на его оси в ту же сторону, куда вращается сам диск, будет вращаться быстрее самого диска, и для того, чтобы удержать ее на этом круговом пути, потребуется большая сила, чем прежде. Если нужного увеличения центростремительной силы не произойдет, то наша частица будет отброшена дальше от оси вращения по отношению к тому месту диска, в котором она находилась. Таким образом, вращение диска приводит к тому, что любая движущаяся по нему частица будет отклоняться под прямым углом к направлению, в котором она первоначально двигалась. Эта отклоняющая сила, именуемая силой Кориолиса (Гаспар Гюстав де Кориолис (1792-1843)-французский инженер и ученый. Он ввел понятие "работы" как произведения силы на путь), особенно влияет на движение ветров.

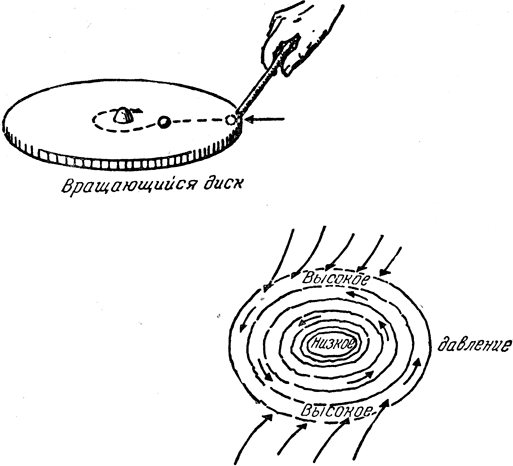
Рис. 3. Как и в опыте с шариком на вращающемся диске, ветры над поверхностью Земли отклоняются, дуя из одного места в другое, из-за вращения нашей планеты. Это вынуждает ветры двигаться по замкнутым линиям, а не дуть по прямой из области высокого давления в область низкого давления

Движение ветров

Ветры дуют в основном из областей высокого давления в области низкого, стремясь выровнять давление в этих областях. Однако при таком движении между областями с разным давлением ветер настолько сильно отклоняется в сторону, что вместо того, чтобы дуть в сторону центра пониженного давления, он движется по окружности вокруг этого центра. По крайней мере именно так обстоит дело в умеренных широтах, в результате чего там образуются системы ветров, дующих вокруг областей пониженного давления и образующих циклоны, и системы ветров, дующих в противоположном направлении вокруг областей повышенного давления, создающие антициклоны. В результате ветер не затихает значительно дольше - до тех пор пока он не перенесет достаточное количество воздуха в область пониженного давления и давления не сравняются. Воздушный поток успевает много раз обежать вокруг центра, и поэтому время жизни областей высокого и низкого давления очень велико. В силу устойчивости этих областей они могут перемещаться далеко в глубь материков; если это области низкого давления, то они принесут с собой дожди в районы, далекие от океана. Главным образом благодаря такому "дрейфу" областей пониженного давления большие пространства материков в умеренных и сравнительно высоких широтах оказываются плодородными и не превращаются в пустыни. Подобным же образом пассаты - ветры, также возникающие вследствие вращения Земли (правда, не совсем так, как циклоны) в областях, примыкающих к экватору, несут влагу в соседние районы континентов. Значит, все особенности существования жизни на Земле и развитие сельского хозяйства зависят от факта вращения Земли. Особенно интересно, что вращение Земли, отклоняя ветры в сторону от их целенаправленного пути, приводит к возникновению ситуации, как раз противоположной тому, чего можно было бы первоначально ожидать: вместо того, чтобы дуть из области высокого давления в область низкого давления перпендикулярно линиям постоянного давления, ветер оказывается направлен почти в точности по изобарам (линиям постоянного давления).

Момент импульса и угловая скорость

Как при поступательном движении тело стремится сохранить это свое состояние и не изменяет своей скорости, пока на него не подействует внешняя сила, точно так же вращающееся тело стремится сохранить свое состояние вращения. Характеристику тела, сохраняющуюся при прямолинейном движении, мы называем импульсом (можно было бы сказать: "линейный момент") и формулируем правило: при отсутствии сил импульс не изменяется. Особенно важно, что это правило можно применять к системе в целом, причем для того, чтобы определить поведение импульса системы в будущем, нет необходимости знать детально ее строение. Единственное, что мы должны знать, это наличие внешних сил. Характеристику же тела, сохранение которой выражает устойчивость вращательного движения, мы назовем моментом импульса (по-другому: "угловой момент"). Тогда, если на тело не действуют силы, стремящиеся замедлить его вращение или закрутить его быстрее (в физике их называют парами или моментами сил), его момент импульса будет сохраняться неизменным.

Но если импульс тела был очень просто связан с его скоростью (пропорционален ей, причем коэффициентом пропорциональности служила масса), то момент импульса и угловая скорость связаны друг, с другом не так просто. Масса остается неизменной, кроме тех случаев, когда какие-то части тела отбра-сываются от него, как это имело место в случае ракеты.

Однако "коэффициент", связывающий момент импульса и угловую скорость, как нетрудно обнаружить, ведет себя сложнее. Если все частицы, составляющие тело, сосредоточены вблизи оси вращения, то они будут двигаться вокруг этой оси с малыми скоростями, даже если тело делает много оборотов в секунду. Если же изменить форму этого тела так, что многие его частицы будут располагаться далеко от оси, то при той же угловой скорости тела движение этих частиц окажется более быстрым. Значит, если отодвинуть массы от оси вращения, то даже при небольшой угловой скорости момент импульса тела будет велик, а если приблизить все массы к оси - момент импульса при той же угловой скорости уменьшится. Поэтому можно изменять угловую скорость, просто сдвигая и раздвигая массы и оставляя момент импульса без изменения. Этим пользуются при фигурном катании на коньках. Искусный конькобежец сначала медленно вращается, раскинув руки в стороны; затем он прижимает руки к себе, стараясь сделаться как можно уже. Поскольку момент импульса конькобежца сохраняется неизменным, угловая скорость его вращения должна сильно увеличиться. Вообще-то все это довольно сложно, и прямо-таки удивительно, как хорошо разбираются в таких вещах кошки - хотя бы даже и инстинктивно.

Падающая кошка

Все знают, что как кошку ни брось, она все равно опустится на лапы. На первый взгляд это кажется удивительным. Если кошку бросили, с самого начала не придав ей вращения, а значит, и момента импульса, то как же она может повернуться лапами вниз? (рис. 4). Ведь для этого ей нужно, падая, какое-то время вращаться, т. е. приобрести угловую скорость, хотя ее момент импульса должен быть все время равен нулю. Как это кошка ухитряется получить угловую скорость, не имея момента импульса? Все объясняется удивительной гибкостью кошки (Фактически движение кошки еще сложнее, чем описано ниже, но основывается оно на изложенных здесь принципах. Движения, которые кошка обязательно должна совершать, мы обсуждаем лишь в общих и основных чертах, чтобы несколько упростить задачу). Предположим, что сначала кошка оттопырит задние лапы, поджав передние и вытянув вперед шею, и станет, скручивая тело, поворачивать переднюю часть туловища. Момента импульса у кошки в целом, конечно, не появится, как его не было и вначале. Но поскольку масса ее задних ног отодвинута далеко от оси вращения, то очень маленькая угловая скорость задней половины тела кошки даст такой же момент импульса, что и большая угловая скорость его передней половины, так как масса передних лап придвинута близко к оси вращения. Направления этих вращений противоположны, и оба момента импульса взаимно уничтожаются, давая полный момент, равный нулю. Однако при этом передняя половина кошки поворачивается в одном направлении гораздо сильнее, чем задняя половина - в противоположном.

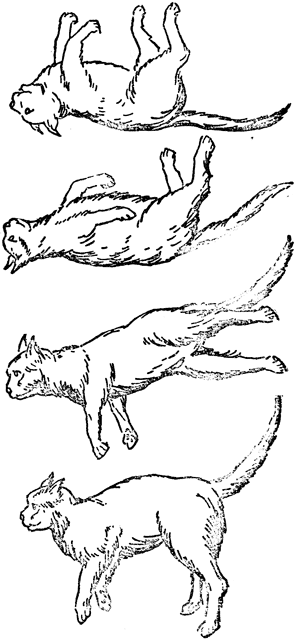
Рис. 4

Затем кошка оттопыривает передние лапы, поджимает задние и перекручивается в обратную сторону. Теперь с большей угловой скоростью движутся задние лапы, а с меньшей - передние, так как задние лапы приближены к оси вращения, а передние удалены от нее. На этом втором этапе передняя часть кошки повернется, конечно, намного меньше, чем ее задняя часть. Когда в конце этого этапа кошка оттопырит задние лапы и подожмет передние, ее положение будет тем же, что в самом начале, только вся она окажется повернутой на заметный угол. Быстро повторяя раз за разом такие движения, кошка пра-вильно ориентирует себя в пространстве и призем-ляется на лапы. На этом примере мы видим, как можно обойти закон сохранения момента импульса, не нарушая его, чего невозможно сделать с импульсом в поступательном движении.

Подведем итог нашим рассуждениям о поступательном и вращательном движении. Выделенное состояние покоя существует во вращательном движении, но в поступательном движении оно отсутствует, Невращающаяся и неускоренная система называется инерциальной. Существует бесчисленное множество инерциальных систем, каждая из которых движется относительно другой инерциальной же системы с постоянной скоростью, прямолинейно и без всякого вращения.

Таким образом, одним из важных следствий ньютоновской физики является заключение о существовании бесчисленного множества инерциальных систем. Как мы увидим дальше, это заключение распространяется без малейшего изменения и на теорию относительности.