8. Природа времени

Теперь все подготовлено для доказательства одного из самых интересных следствий теории относительности, а именно, что время - это величина, зависящая от пути. Для этого нам нужно рассмотреть предметы, движущиеся с очень большими скоростями, сравнимыми со скоростью света. Мы никогда не встречали таких объектов в повседневной жизни и никогда не встречались с путешественниками, которым случалось бы летать с такими большими скоростями друг относительно друга. Поэтому нам придется рассматривать непривычные и потому странные ситуации. Однако у нас нет выбора. В больших ускорителях элементарные частицы иногда разгоняются более чем до 99% скорости света, и физик должен разобраться в условиях, которые сопутствуют этим скоростям. Кроме того, летящие с такими скоростями частицы нам попадаются в космических лучах. Из-за технических трудностей мы можем разгонять до таких скоростей лишь атомные частицы, и их собственные необычные свойства складываются тогда с теми необычными качествами, которые вызваны их большими скоростями. Но ведь наше воображение не ограничено возможностями современной техники. И по крайней мере для целей нашей беседы мы можем выделить отдельно все необычное, проявляющееся при больших скоростях, позволив себе поставить на место атомных частиц людей, движущихся с такими скоростями.

Специфика больших скоростей

Поскольку нам потребуются инерциальные наблюдатели, они должны двигаться с постоянными скоростями. Чтобы нам не приходилось думать об ужасно коротких промежутках времени, этим наблюдателям нужно дать много места, - можно представить себе их как космонавтов, мчащихся в просторах вселенной гораздо быстрее, чем могут двигаться современные ракеты. Такая выдумка поможет сделать наши рассуждения более доходчивыми. Мы разъясним содержание принципа относительности и затем выведем из него следствия, которые можно наблюдать, так что останется лишь потребовать их проверки путем проведения соответствующих экспериментов.

Напомним, что эйнштейновский принцип относительности утверждает равноправие всех инерциальных (движущихся равномерно и прямолинейно) систем. Уже ньютоновская механика указывает на важность ускорения и несущественность скорости (налить чашку чая в плавно летящем реактивном самолете нисколько не сложнее, чем у себя дома) - таким образом определяются инерциальные системы. Механика Ньютона утверждает эквивалентность этих инерциальных систем (в своих механических рамках). Но в предыдущих главах, подчеркивая единство физики, мы выяснили, каким все было бы нелепым, если бы в разных областях физики действовали разные правила перехода (преобразования) от одного инерциального наблюдателя к другому. Это привело нас к эйнштейновскому принципу полного равноправия всех инерциальных наблюдателей, и мы займемся теперь отысканием следствий из этого принципа, исходя из простых идеализированных опытов.

Наших движущихся наблюдателей лучше изображать, говоря жаргоном этой теории, на пространственно-временных графиках (рис. 12). На этих графиках вертикальная ось изображает время, измеряемое некоторым инерциальным наблюдателем, а горизонтальная ось изображает расстояние в пространстве. К счастью, почти для всех наших выводов будет достаточно всего одного пространственного измерения, т. е.; все рассматриваемые предметы движутся вдоль одной прямой.

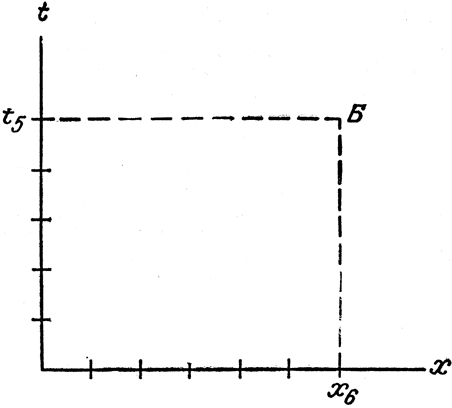
Рис. 12. Пространственно-временной график

Связь между покоящимся и движущимся наблюдателями

Если график рисует наблюдатель А, то он, понятно, изобразит себя в начале системы координат. Иначе говоря, он приурочит свои наблюдения к тому моменту, когда его время равно нулю, и станет определять положение других наблюдателей (как во времени, так и в пространстве) относительно своего собственного положения в тот момент, когда его время равно нулю. Поскольку он считает, что находится в покое, а значит, не движется никуда по пространственной оси (оси расстояния), то его координата х остается равной нулю. Отрезки вдоль оси t, изображающие истекшее время, показывают положения А на схеме нашего опыта, причем нужно помнить, что отрезки вдоль оси t измеряет именно А.

Например, чтобы измерить положение наблюдателя Б в момент 0+5 и на расстоянии в 6 единиц, А отсчитает 5 единиц вверх по оси t и 6 единиц по оси х, построит в полученных точках перпендикуляры к соответствующим осям и на их пересечении отметит на своем пространственно-временном графике положение Б. Так наблюдатель А устанавливает по отношению к себе положение Б в данный момент времени и при заданном расстоянии.

Если Б также является инерциальным наблюдателем, то, по нашему определению, он движется с постоянной скоростью и проходит равные отрезки пути за равные промежутки времени. Значит, все положения Б на пространственно-временном графике будут лежать на прямой линии, и подобным же образом любой другой инерциальный наблюдатель может быть изображен прямой линией (Однако читатель должен помнить, что хотя пространственно-временные схемы очень хорошо показывают, кто, где и когда находится, они всего лишь графические изображения, выполненные одним из наблюдателей. Времена и расстояния, прожитые и измеренные другими наблюдателями, невозможно определить, измеряя длины на таких схемах).

Рис. 13 - это пространственно-временной график А, изображающий также четырех других наблюдателей. Обратите особое внимание на разную крутизну (или наклон, если пользоваться принятым в математике выражением) прямых, изображающих наблюдателей Б, В, Г, Д. Чем круче линия, тем меньше изменяется х при заданном изменении t и тем медленнее движется соответствующий наблюдатель относительно А (тем меньший путь он проходит за данное время). Значит, Б движется в сторону от А довольно медленно, а В - несколько быстрее; в то же время Д, х-координата которого постоянна, покоится относительна А. И Б и В движутся в сторону от А, потому что стечением времени (т. е. вверх по схеме) и х-координаты растут. Напротив, Г приближается к А. Линия, соответствующая движению света, который распространяется очень быстро, наклонена гораздо сильнее, так что прерывистой линией мы изобразили распространение вспышки света.

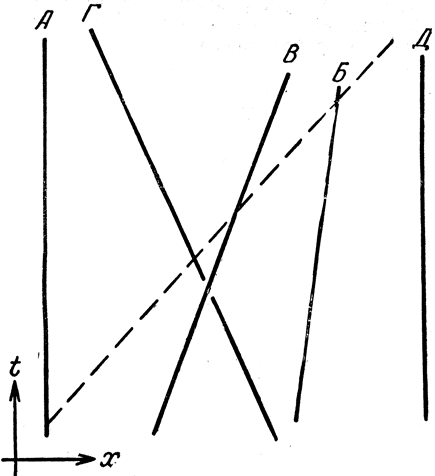
Рис. 13

Свет - это волновое явление. В гл. 5 мы рассмотрели другое волновое явление - звук, обратив особое внимание на эффект Допплера, т. е. различие в высоте звука при его лосылке и при приеме, вызываемое относительным движением источника звука и наблюдателя. Вы помните, что в случае звука было необходимо знать как скорость излучателя относительно воздуха, так и скорость приемника относительно воздуха. В случае света нет ничего такого, что играло бы роль воздуха, так что нам необходимо знать лишь скорость излучателя относительно приемника. Мы считаем при этом, что оба они движутся по инерции, т. е. с постоянными скоростями.

Пусть два наблюдателя находятся на неизменном расстоянии друг от друга, и первый из них, по имени Арнольд, через одинаковые промежутки времени включает электрический фонарик (рис. 14). Только для определенности и не придавая этому какого-либо особого значения, предположим, что он посылает световые вспышки каждые 6 мин по его часам. Свет каждой вспышки доходит до второго наблюдателя - Глеба. Поскольку расстояние между наблюдателями с течением времени не изменяется, то время распространения каждой вспышки должно быть одним и тем же. Значит, если Арнольд по своим часам зажигает фонарик каждые 6 мин, то Глеб будет видеть вспышки через равные промежутки времени - тоже каждые 6 мин (по часам Глеба). Мы считаем, что расстояние между Арнольдом и Глебом велико. Может быть, свет дойдет до Глеба через 10 лет (ведь это - идиализированный опыт), но важно только то, что, сколько бы времени он ни шел, все вспышки будут следовать друг за другом через каждые б мин. Ничего особенно в этом нет, и к тому же оба наблюдателя могут поменяться местами - картина от этого не изменится.

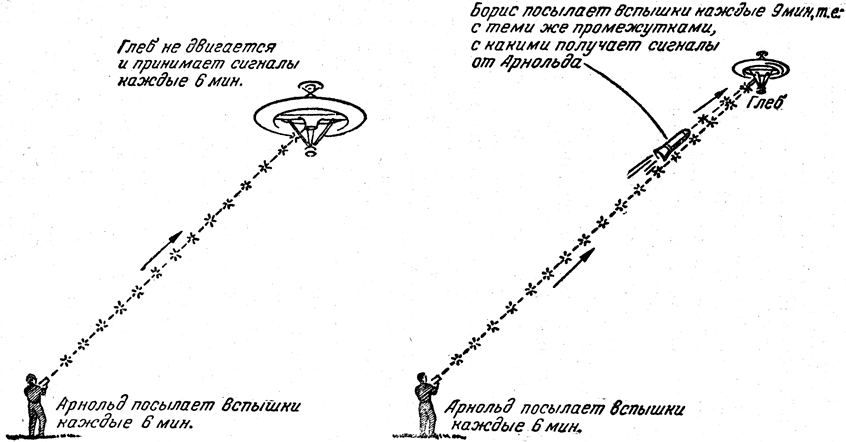
Рис. 14

Введем теперь третьего наблюдателя - Бориса, который очень быстро движется от Арнольда к Глебу, а те двое продолжают покоиться по отношению друг к другу. (См. рис. 15; мы советуем читателю держать книгу открытой на этом рисунке, пока он разбирается во всех рассуждениях.) Двигаясь от Арнольда к Глебу, Борис тоже наблюдает вспышки. Поскольку он удаляется от Арнольда, то каждой следующей вспышке приходится проходить до него большее расстояние, чем предыдущей, и она тратит на это больше времени. Поэтому по часам Бориса вспышки будут приходить не каждые 6 мин, а через большие промежутки времени - просто потому, что свету от каждой вспышкй приходится проходить больший путь, чем от предыдущей. При соответствующей скорости, которую мы пока не будем пытаться уточнять, вспышки могут приходить к Борису, например, через каждые 9 мин по его часам. Мы постоянно подчеркиваем, что каждый наблюдатель узнает время прихода вспышек по своим собственным часам; ведь иначе нам пришлось бы помучиться, думая, сколько времени он затратит на то, чтобы взглянуть на часы своего приятеля.

Предположим теперь, что у Бориса тоже есть фонарик, например красный, которым он мигает каждый раз, увидев вспышку от Арнольда. Раз Борис видит эти вспышки каждые 9 мин, то он посылает красные сигналы тоже каждые 9 мин. Эти красные вспышки дальше будут лететь вместе с белыми вспышками Арнольда, потому что они были испущены в те самые моменты, когда свет от Арнольда проходил мимо Бориса (мы пренебрегаем тем временем, которое требуется, чтобы включить фонарик). Эти сигналы Бориса, идущие вместе с сигналами Арнольда, увидит Глеб, который наблюдает вспышки Арнольда (т. е. белые вспышки) каждые 6 мин. Значит, и красные вспышки он будет наблюдать каждые 6 мин. Выразим все это немного иначе.

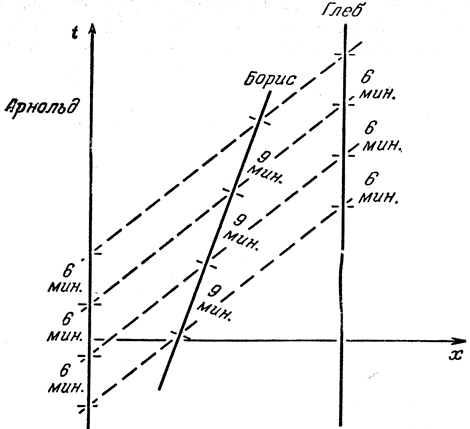
Рис. 15. Отношение между интервалами приема и интервалами передачи сигналов равно 1 для Арнольда и Глеба, которые покоятся друг относительно друга, ³/₂ для Арнольда и Бориса и ²/₃ для Бориса и Глеба

Арнольд и Борис удаляются друг от друга с определенной скоростью, а именно с такой, что промежутки времени между вспышками Арнольда нужно умножить на ³/₂, чтобы получить интервалы, с которыми Борис видит эти вспышки (9 мин вместо 6). Борис летит навстречу Глебу с той же скоростью, с какой он улетает от Арнольда, но теперь это скорость сближения, а не удаления, и те вспышки, которые излучались каждые 9 мин, будут поступать каждые 6 мин, т. е. чаще, все с тем же коэффициентом (лучше сказать: теперь мы множим на ²/₃). Если бы Борис мигал своим фонариком каждые 6 мин, то Глеб видел бы вспышки соответственно с 4-минутными промежутками. Значит, если взять вместо скорости удаления скорость приближения, то множитель ³/₂, переводящий интервалы между моментами излучения в интервалы между моментами приема вспышек, заменится на множитель ²/₃. Этот вывод совершенно не зависит от того, может ли кто-либо из этих наблюдателей считаться покоящимся (неподвижным) или нет. Даже наоборот, вывод не изменится, кого бы из наблюдателей мы ни считали неподвижным. Существенна лишь относительная скорость наблюдателей. Все, что следует нам усвоить, - это вывод: если какая-то скорость удаления приводит к некоторому соотношению между интервалами передачи и интервалами приема сигналов, то такая же скорость приближения дает в точности обратное соотношение.

Дадим этому выводу более общее выражение. Пусть Арнольд мигает своим фонариком с интервалами h; тогда Глеб должен увидеть вспышки с интервалами h, так как каждая вспышка тратит одно и то же время на путь от Арнольда к Глебу. Борис увидит их через некоторый интервал kh уже по своим часам, и здесь k - это отношение между интервалами при приеме и при передаче. Если Борис (глядя на свои часы) станет мигать своим фонариком с интервалами kh, то эти вспышки, двигаясь вместе со вспышками, передаваемыми Арнольдом, будут приняты Глебом с интервалами h, откуда для соотношения Борис - Глеб получается обратная величина l/k.

Связь между каждыми двумя инерциальными наблюдателями у нас полностью определяется отношением между интервалами приема и интервалами передачи. Когда это отношение равно единице (как было в случае Арнольда и Глеба), то оба наблюдателя неподвижны относительно друг друга; если оно больше единицы, то наблюдатели удаляются друг от друга, а если меньше - приближаются друг к другу. Важно, что из принципа относительности, устанавливающего эквивалентность всех инерциальных наблюдателей, со всей ясностью вытекает, что это отношение должно быть одним и тем же, какого бы именно наблюдателя из данной пары инерциальных наблюдателей мы ни заставили посылать сигналы. Как раз отсюда видно, что положение со светом так сильно отличается от положения со звуком (гл. V), когда, как вы помните, нужно было учитывать и скорость передатчика, и скорость приемника относительно воздуха.

Более сложный случай

Теперь мы уже можем применить наш вывод к более сложному случаю (важны отношения между интервалами; каждое отношение зависит только от движения данной пары наблюдателей; при сближении наблюдателей отношение будет обратным величине отношения для их удаления). Присоединим нового наблюдателя - Вадима (теперь мы обойдемся без Глеба), имеющего относительно Арнольда ту же скорость, что и Борис, только направленную противоположно (рис. 16 и табл. 2). Этот наблюдатель тоже движется по инерции. Пусть, кроме того, Борис пролетает мимо Арнольда в 12 час дня по часам Бориса, а Вадим встречает Бориса в 1 час дня - тоже по часам Бориса. Несколько позднее Вадим пролетает мимо Арнольда. Поскольку скорости Вадима и Бориса относительно Арнольда одинаковы, а положение этих двух наблюдателей симметрично относительно Арнольда, то по часам Вадима должен пройти 1 час между его встречами с Борисом и с Арнольдом. Общая картина такова, что в течение всего опыта Арнольд, Борис и Вадим находятся на одной прямой. Сначала Борис был слева от Арнольда, а Вадим справа, но намного дальше, чем Борис. И Борис и Вадим приближаются к Арнольду с одной и той же скоростью. События происходят в таком порядке: сначала Борис пролетает мимо Арнольда, затем Борис встречается с Вадимом и, наконец, Вадим пролетает мимо Арнольда. После этого Вадим будет слева от Арнольда, а Борис намного дальше, чем Вадим, справа от Арнольда. И Борис и Вадим теперь удаляются от Арнольда.

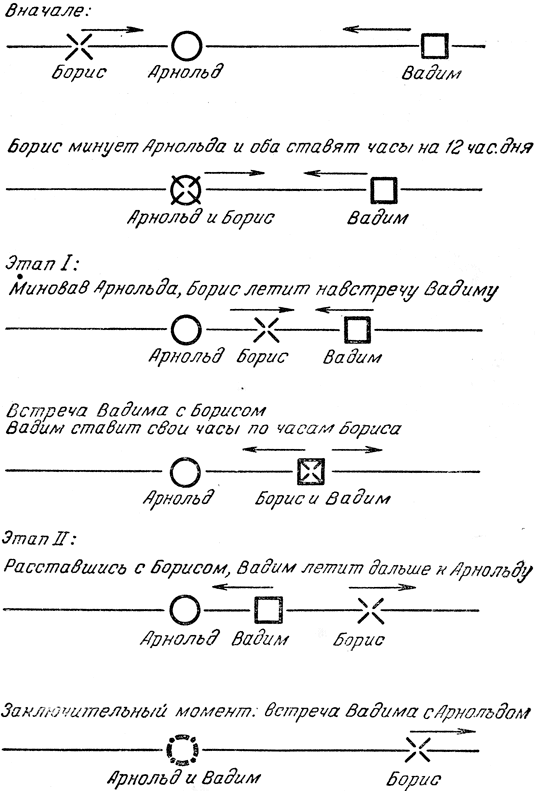
Рис. 16. Последовательность событий

Сосредоточим свое внимание на этих трех ветречах (первая - Арнольда и Бориса, вторая - Бориса и Вадима, третья - Вадима и Арнольда). Как уже установлено, между первыми двумя встречами прошел 1 час по часам Бориса, который участвовал в обеих этих встречах. Подобным же образом между двумя последними встречами прошел 1 час по часам Вадима, который на этот раз участвовал в обе-их встречах (рис. 17). Пусть теперь Вадим поставит свои часы так, чтобы они показывали то же время, что и часы Бориса в момент их встречи. Это было в 1 час дня, так что при встрече с Арнольдом он отметит 2 час дня. Пусть и Арнольд поставит свои часы по часам Бориса при своей встрече с ним, когда было 12 час. Возникает вопрос: что будут показывать часы Арнольда в момент его встречи с Вадимом? Если это будет не 2 час дня (а мы это докажем!), т. е. если его часы будут показывать другое время, чем часы Вадима, то, значит, мы докажем зависимость времени от пути. Эта зависимость от пути будет несколько другого сорта, чем в случае километража. Она будет определяться сближением или удалением наблюдателей, иными словами, переходом от одного инерциального наблюдателя к другому, в противоположность случаю, когда мы имеем дело с одним и тем же инерциальным наблюдателем (Арнольдом).

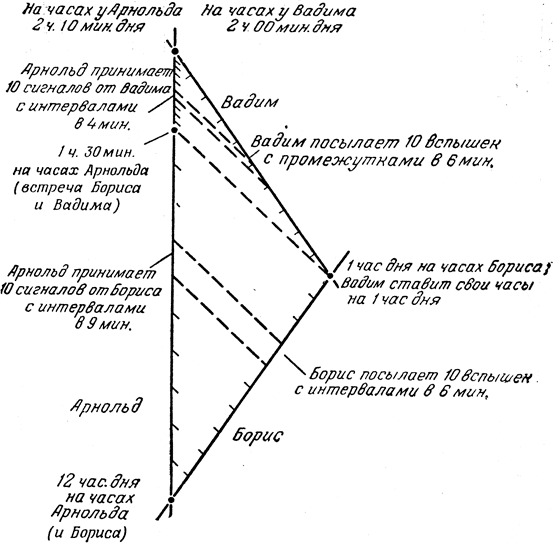
Рис. 17

Чтобы выяснить ход времени у Арнольда, предположим теперь, что Борис, начиная с момента своей встречи с Арнольдом, каждые 6 мин по своим часам посылает световой сигнал; последний сигнал он посылает при встрече с Вадимом. Между этими встречами по часам Бориса прошел ровно 1 час, так что последовало как раз 10 интервалов между вспышками. Взяв скорость удаления друг от друга Арнольда и Бориса такой же, как и в предыдущем примере, мы обнаружим, что Арнольд будет принимать эти вспышки по своим часам каждые 9 мин. Часы Арнольда показывали 12 час дня, когда пришла первая вспышка - ведь Борис в этот момент был рядом с ним, так что передача и прием сигнала произошли практически одновременно. Последняя же вспышка пришла к Арнольду через 90 мин - в 1 час 30 мин дня по его часам, В этот момент до него дошел свет с места встречи Бориса и Вадима, т. е. в этот момент он "увидел" их встречу.

Таблица 2. Последовательность событий

Предположим теперь, что и Вадим посылает каждые 6 мин по своим часам световые сигналы - первый, когда он встретился с Борисом, и последний, когда он минует Арнольда. Их будет 10, потому что путь займет у него 1 час. Из предыдущего примера ясно, что Арнольд должен принимать эти вспышки каждые 4 мин, потому что Вадим приближается к нему точно с той же скоростью, с какой Борис приближался в том примере к Глебу. Значит, по часам Арнольда эти 10 интервалов между вспышками займут 40 мин. Первая вспышка пришла к нему в 1 час 30 мин по его часам, потому что она была послана, когда Вадим встретил Бориса, а свет с места их встречи пришел к Арнольду в 1 час 30 мин по его часам. Поскольку последняя вспышка долетела по часам Арнольда через 40 мин, его часы должны в этот момент показывать 2 час 10 мин дня. Но ведь Вадим послал последний сигнал, когда сблизился с Арнольдом, а это случилось по часам Вадима в 2 час дня! И оба наблюдателя были так близко друг к другу, что свет практически не затратил времени, чтобы пройти расстояние между ними - встреча по часам Вадима произошла в 2 час дня, а по часам Арнольда - в 2 час 10 мин дня.

Подведем итоги. Первое из рассмотренных событий - встреча Арнольда и Бориса, когда оба эти наблюдателя поставили свои часы на 12 час дня. Борис послал тогда свой первый сигнал, сразу же принятый Арнольдом. Вслед за этим Борис удалялся от Арнольда, а Вадим приближался к Арнольду, оставаясь от него дальше, чем Борис. На этом этапе, продолжавшемся, согласно часам Бориса, 1 час, Борис посылал каждые 6 мин световые сигналы, которые поступали к Арнольду через каждые 9 мин (отношение ³/₂). В конце этого этапа часы Бориса показывают 1 час дня, и Вадим пролетает мимо него, поставив свои часы по часам Бориса. Вадим сразу же начинает посылать вспышки света с интервалами в 6 мин. Последняя вспышка Бориса, испущенная при этой встрече, летит вместе с первой вспышкой Вадима, и обе они приходят к Арнольду в 1 час 30 мин дня по часам Арнольда (10 интервалов, каждый продолжительностью по 9 мин, первый из которых начался в 12 час дня).

На втором этапе Вадим приближался к Арнольду, посылая световые сигналы каждые 6 мин (Борис нас больше не интересует, мы следим только за Вадимом). Арнольд принимает сигналы Вадима каждые 4 мин (отношение ²/₃). Пропутешествовав 1 час по своим часам после встречи с Борисом, Вадим встречается с Арнольдом. Значит, по часам Вадима эта встреча произошла в 2 час дня. Десять интервалов между вспышками Вадима занимают 40 мин по часам Арнольда. Раз первая из них пришла в 1 час 30 мин дня по времени Арнольда, то последняя (отправленная Вадимом, когда он пролетал мимо Арнольда) пришла в 2 час 10 мин дня, и это было то время по часам Арнольда, когда он встретил Вадима (см. рис. 16 и табл. 2).

Теория относительности объясняет кажущееся противоречие

Кто же прав? Конечно, мы ответим, что правы оба. Ведь если, например, два шофера поедут от Нью-Йорка до Бостона, и один насчитает 370, а другой - 400 км, то мы же не скажем, что один из нлх ошибся, а просто подумаем, что один ехал по более короткому пути. Незачем даже валить вину на спидометр. Нам остается тогда признать, что время, подобно расстоянию, зависит от пути. Время от первой до последней встречи, измеренное Борисом и Вадимом, короче, чем время от первой до последней встречи по измерению Арнольда.

Нечего и думать, будто скорость "подействовала" на часы Бориса и Вадима. Это было бы так же нелепо, как если бы мы заявили, будто кружной путь, выбранный одним из шоферов, так "подействовал" на его спидометр, что он стал показывать больше, чем счетчик на спидометре другой машины. Дело не в том, что что-то не в порядке со спидометрами или с часами, а просто в том, что время - такая же зависящая от пути величина, как и расстояние (километраж). Мы обнаружили, что принцип относительности не позволяет сохранить представление о времени, как о величине, не зависящей от пути, а значит, и представление о существовании всеобщего времени. Существует только индивидуальное время - время, зависящее от пути, выбранного между событиями, так как мы могли выбирать, идти ли нам вместе с Арнольдом или пойти с Борисом, а потом с Вадимом.

Обнаружив это, некоторые запутываются и возражают: "Но ведь можем же мы с тем же основанием считать Бориса покоящимся, а Арнольда движущимся, как мы считали Арнольда покоящимся, а Бориса движущимся". Это именно так, и никто с этим не спорит; единственное, чего мы не можем предположить в этом примере, так это, что и Борис и Вадим неподвижны. Этот эксперимент невозможно повернуть так, чтобы появилась симметрия между Арнольдом, с одной стороны, и Борисом и Вадимом - с другой. Арнольд здесь всего один, а Борис и Вадим - это двое, и как бы мы не оборачивали условия этой задачи, покоиться всегда может лишь один из троих. Одно из измерений всегда производит сам Арнольд, а другое - это комбинация, совокупность измерений Бориса и Вадима.

Величина k - фундаментальное отношение

Ясно, что полученное расхождение на 10 мин за 2 час очень сильно зависит от скорости. Подойдем теперь к этому вопросу с более общих позиций. Предположим, что отношение между интервалами приема и интервалами передач сигналов для Бориса и Арнольда равно Как мы доказали раньше, для Вадима и Арнольда тогда оно будет равно 1/k.

Предположим теперь, что Арнольд и Борис оба поставили свои часы на ноль в момент своей встречи, и примем, что на часах Бориса было 0+T час в тот момент, когда мимо него промелькнул Вадим. В этот же момент Вадим поставил свои часы по часам Бориса, так что на них стало 0+T. Вадим понесся навстречу Арнольду с той же самой скоростью, с какой от того удалялся Борис. Поэтому, для того чтобы долететь до Арнольда после встречи с Борисом, Вадиму потребовалось то же самое время Т, какое потребовалось Борису, чтобы долететь до Вадима после встречи с Арнольдом. Значит, в момент встречи с Арнольдом часы Вадима показывали 0+Т+Т, т. е. 2Т (см. табл. 3).

Таблица 3. Последовательность событий

Пусть Борис послал световой сигнал в момент встречи с Арнольдом, а затем - в момент встречи с Вадимом, т. е. с интервалом Т по часам Бориса. Когда эти сигналы принял Арнольд, то по его часам промежуток между ними должен быть равным kT. Поскольку первому сигналу не пришлось преодолевать никакого расстояния, ибо он был дан в момент наибольшего сближения Бориса с Арнольдом, то он был принят сразу же, в момент 0 по часам Арнольда, а второй сигнал пришел в kT час по времени Арнольда. Подобным же образом Вадим дал два сигнала в моменты обеих встреч. По часам самого Вадима промежуток между ними составлял Т, но поскольку Вадим приближался к Арнольду, последний принял их с интервалом T/k. Первая вспышка от Вадима была послана из того же места и в тот же момент, что и вторая вспышка от Бориса, т. е. при их встрече, и, распространяясь вместе с ней, она дошла до Арнольда в момент kT по часам Арнольда. Поэтому вторая вспышка от Вадима шла к Арнольду в течение (1/k)T час по времени Арнольда. Этот последний сигнал был дан Вадимом, когда тот подлетел вплотную к Арнольду, т. е. он дошел тотчас же. Значит, часы Арнольда показывали время (k+1/k) Т в тот момент, когда на часах Вадима было 2Т час. Итак, отношенние промежутка времени между встречами Бориса и Вадима с Арнольдом, измеренного Арнольдом, к этому же промежутку, измеренному Борисом и Вадимом, равно

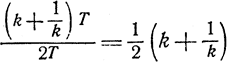
Это отношение очень чувствительно к изменениям величины k, как это видно из табл 4, в которой приведены также различия между показателями часов Арнольда и Вадима для случая Т=1 час.

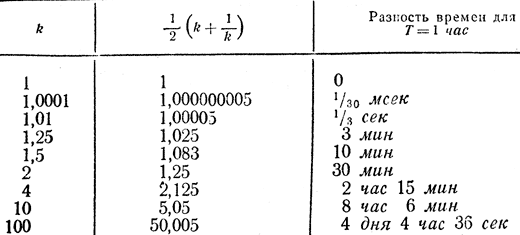
Таблица 4

Хотя связь между величиной k и скоростью будет выведена лишь в следующей главе, не мешает здесь заметить, что значение k=1,0001 соответствует скорости 30 км/сек, равной скорости Земли при ее движении по орбите и почти в четыре раза превышающей скорость искусственного спутника Земли, тогда как скорость, соответствующая k=10, равна 90% скорости света, a k=100-99,98% скорости света.

В нашей практической жизни коэффициент k всегда так ничтожно мало отличается от единицы, что расхождение часов не может играть ровно никакой роли. Именно это и подкрепляет ложное ощущение, будто время не зависит от пути.

Допустим теперь, что Борис путешествовал со своим маленьким сыном, которому он доверил свои часы, и, когда мимо него проносился Вадим, Борис перебросил сына ему. Пусть Вадим осторожно поймал его и взял с собой в свое путешествие к Арнольду. Вот здесь мы можем поинтересоваться: "А не будет ли все равно: считать покоящимся Арнольда, а путешествующим мальчика, или рассматривать неподвижным мальчика, предоставив путешествовать Арнольду?" Вот это-то и неверно! Ведь все трое - Арнольд, Борис и Вадим - инерциальные наблюдатели, не испытывающие никаких рывков, и если у кого-нибудь из них была в начале нашего эксперимента корзинка с сырыми яйцами, то в конце в ней все было бы в порядке. А вот мальчик - не инерциальный наблюдатель, его скорость неожиданно и резко изменилась, он ощутил мощный рывок. Если бы с ним послали эту корзинку с сырыми яйцами, то под конец там была бы сплошная яичница! Его никак нельзя сравнивать с Арнольдом, инерциальным наблюдателем. Между ними нет никакой симметрии, и понять это нетрудно, так что противоречий не возникает. Если окажется, что толчок при переброске от Бориса к Вадиму не оказался роковым для мальчика или для его часов, о чем мы еще поговорим в одной из следующих глав, то в момент последней из встреч мальчик будет на 2 час старше, чем при первой, тогда как Арнольд постареет на 2 час 10 мин.

Это нам следует снова сравнить с километражем: из всех расстояний между двумя городами самое короткое - это расстояние по прямой, а все другие пути будут длиннее. В отношении времени теория относительности утверждает обратное: время между двумя событиями, измеренное инерциальным наблюдателем, - максимальное (наибольшее), а время между ними, измеренное любым другим (неииерциальным) наблюдателем, - более короткое. Значит, путешествуя, можно было бы оставаться молодым, если бы только не те острые ощущения, которые придется испытать, когда Борис будет тебя перебрасывать Вадиму. Относительные скорости, с которыми двигались наблюдатели в этом примере, мы подсчитаем в следующей главе. Ясно, что они весьма велики - много тысяч километров в секунду. Такие скорости настолько далеки от испытываемых нами в обыденной жизни, что нисколько не удивительно, какими непривычными для нас должны быть проявления этих необычных условий.