
9. Скорость
В двух предыдущих главах мы узнали очень многое об инерциальных наблюдателях, задавшись величиной отношения между промежутками времени в приеме двух световых сигналов одним наблюдателем и в излучении их - другим. Но как связать это столь важное для всех наших выводов отношение со скоростью наблюдателей друг относительно друга? Ведь перейти к скорости - значит перейти к гораздо более привычной и понятной нам величине.
Вернемся к героям предыдущей главы - Арнольду и Борису, движущимся относительно друг друга. Чтобы идти в ногу с веком, вооружим их вместо фонариков радиолокаторами (в принципе это одно и то же) и допустим, что, получив сигнал от Арнольда, Борис сразу же сигналит ему своим лучом. Как мы увидим, эта картина не отличается от случая, когда мы посылаем радиолокационный импульс и вновь принимаем его после отражения от поверхности Луны или какого-нибудь искусственного спутника, положение которого нам требуется точно определить (рис. 18).
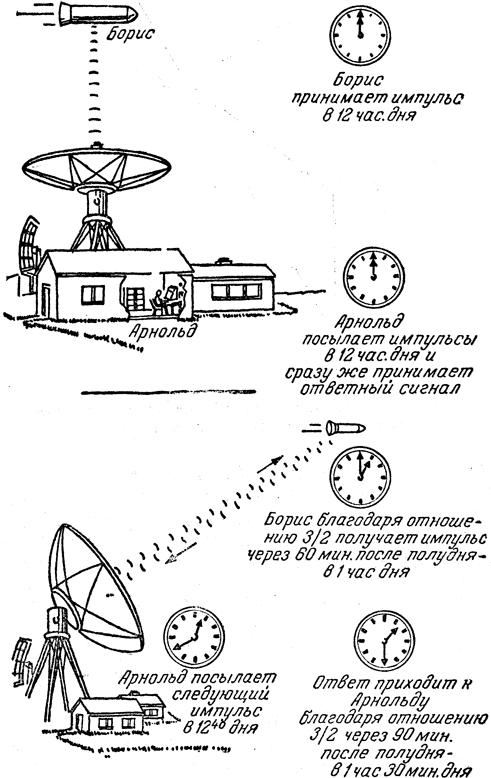
18. Арнольд измеряет скорость Бориса (отношение интервалов 3/2)
Поскольку мы придали отношению между интервалами приема и интервалами передачи величину 3/2, то сигналы Арнольда, отправленные с промежутками в 6 мин, поступают к Борису каждые 9 мин. Мы приняли также, что в момент пролета наблюдателей друг мимо друга их часы показывали одно и то же время - 12 час дня. Значит, если Арнольд отправит первый импульс в 12 час, а второй - в 12 час 40 мин дня, то эти сигналы придут к Борису с интервалом в 60 мин (по часам Бориса), как это изображено на рис. 19. Так как Борис повстречался с Арнольдом в 12 час по времени Арнольда, то первый сигнал Арнольда дошел до него в этот же момент (в 12 час дня и по его часам) второй - в 1 час дня, как раз когда он встретился с Вадимом. Борис сразу же отправил обратный сигнал, и этот ответ, посланный по его часам через 60 мин после полудня, был получен Арнольдом (согласно пропорции 3/2) через 90 мин после полудня (рис. 19). Вспомнив наши рассуждения на стр. 77-79, мы должны иметь в виду, что ни Арнольд, ни Борис не могут утверждать категорически, что кто-то из них покоится, а другой движется: они имеют право лишь сказать, что удаляются друг от друга. Именно поэтому отношение 3/2 относится к обоим направлениям посылки сигналов. Значит, Арнольд послал радиолокационный импульс в 12 час 40 мин дня, а отраженный импульс вернулся к нему в 1 час 30 мин дня - на 50 мин позже. Следовательно, для путешествия от Арнольда до Бориса и назад сигналу потребовалось 50 мин; пройденное им расстояние в два раза больше расстояния между этими наблюдателями. Мы видим, что на путешествие от Арнольда до Бориса свет (или радиолокационный импульс) потратил половину этого времени - 25 мин, так что расстояние до Бориса в момент, когда он отвечал, равнялось 25 световым минутам.
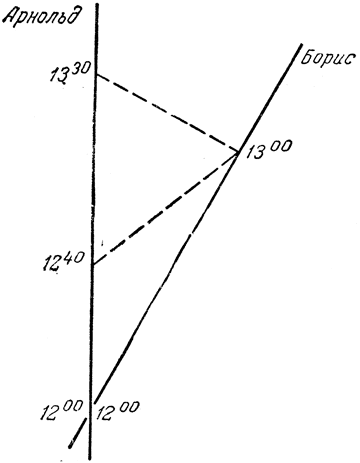
Рис. 19. Пространственно-временная схема, изображающая, как Арнольд измеряет скорость Бориса
Сколько же времени потребовалось Борису (но по часам Арнольда), чтобы улететь на такое расстояние? Момент времени, который Арнольд связывает с отражением своего сигнала, должен быть посередине между моментом его посылки и обратного приема, т. е. посередине между 12 час 40 мин и 1 час 30 мин дня - в 1 час 05 мин дня. У Арнольда нет никакой иной возможности, кроме выбора этого момента для отражения импульса. Поскольку скорость света по определению равна единице, то в представлении Арнольда свету было нужно ровно столько же времени, чтобы дойти до Бориса, сколько и для того, чтобы вернуться назад. И уж во всяком случае ему не следует пытаться вводить "поправку" на скорость Бориса. Ведь этот импульс вернулся бы в тот же самый момент и в том случае, если бы он отразился от предмета, двигавшегося совсем иначе, чем Борис, но просто оказавшегося рядом с ним в момент отражения. Поэтому Арнольду ничего не остается делать, кроме как принять для этого события время в 1 час 05 мин дня. Таким образом он пришел к выводу, что Борису потребовалось 65 мин (с 12 час до 1 час 05 мин дня) для того, чтобы пройти расстояние, которое свет проходит за 25 мин. Значит, скорость Бориса относительно него составляет 25/65=5/13 скорости света в исчислении Арнольда. Если взять общепринятое значение для скорости света, то эта дробь, выражающая скорость движения Бориса относительно Арнольда в долях скорости света, равна 115 400 км/сек - величина, весьма почтенная по нашим понятиям, однако отнюдь не невозможная. В силу сделанных нами предположений скорость Вадима относительно Арнольда имеет в точности ту же величину.
Длинные поезда Эйнштейна
Статья Эйнштейна по специальной теории относительности, которой посвящены эти страницы, вышла в 1905 г. Самолет поднялся в воздух всего за два года до этого, и поезд был самым быстрым средством сообщения. Казалось в высшей степени невероятным, чтобы транспорт когда бы то ни было превысил скорость 200 км/час. Когда в 1916 г. Эйнштейн писал книгу о теории относительности, предназначенную им для массового читателя, он не мог найти лучшего примера для иллюстрации своих мыслей, чем воображаемый бесконечно длинный поезд, мчащийся мимо бесконечно длинной платформы со скоростью, приближающейся к световой. Все авторы, пытавшиеся вслед за ним в течение более чем сорока лет популяризовать теорию относительности, пользовались тем же примером. Даже в книге Бертрана Расселла "Азбука теории относительности", изданной в 1958 г., различные вопросы обсуждаются на примере поезда, несущегося со скоростью, равной 3/5 скорости света, по прямолинейному пути бесконечной длины. У этих авторов не было выбора. Какими бы надуманными ни казались эти поезда, они представлялись авторам почти что единственным примером, доступным пониманию простого читателя и не кажущимся ему какой-то фантастической чепухой. После этого неудивительно, что широкая публика считала теорию относительности в лучшем случае бесполезными умозрениями оторванных от жизни мыслителей, а в худшем - наукообразными домыслами.
Сейчас все переменилось. Мы посылаем ракеты к Луне, Марсу и Венере. Самый твердолобый скептик уже не сомневается в том, что при жизни самых юных читателей этих страниц космические станции станут реальностью. Советские и американские космонавты уже кружатся вокруг Земли со скоростью почти 30 000 км/час - и хотя скорость нашего Бориса в 115 400 км/сек намного превышает эту скорость, мы все же можем теперь более реалистично представлять себе те скорости, которых никак не могло постичь сознание наших отцов и дедов. Экспериментаторы на больших ускорителях ежедневно имеют дело со скоростями в 9/10 световой, так что их профессия является чисто релятивистской и они каждый день сталкиваются с эффектами теории относительности. За несколько лет специальная теория относительности спустилась с облаков фантазии и философского умозрения на твердую почву всеобщих потребностей и интересов.
Человеческому уму свойственно усваивать что-то с большей легкостью, если имеется явная потребность в усвоении этого. У наших отцов не было истинной потребности понять теорию относительности, но у нас она уже есть, и мы можем обратиться к приключениям Арнольда, Бориса и Вадима, не испытывая того ощущения неправдоподобности, которое смущало пассажиров бесконечно длинных поездов Эйнштейна. Хотя наши Арнольд, Борис и Вадим - не менее фантастические персонажи, все же их путешествие в космосе отражает те условия, с которыми - пусть более сложно и технически совершенно, чем это описывали мы, - сталкиваются и работают современные ученые и инженеры в своих лабораториях. Теперь, помня, что мы разбираем смысл вполне реальных понятий, вернемся к нашим трем инерциальным наблюдателям, столкнувшимся с разнообразием времен в специальной теории относительности.
Определение относительных скоростей с помощью радиолокатора
Возьмем снова движение наших наблюдателей из гл. 8, но рассмотрим несколько видоизмененный случай. Пусть снова Борис и Вадим движутся с одинаковой по величине скоростью относительно Арнольда и пусть между встречами Бориса с Арнольдом и с Вадимом промежуток времени равен одному часу, с точки зрения Бориса, а между встречами Вадима с Борисом и Арнольдом - тоже одному часу, но уже по часам Вадима. Пусть теперь, однако, наш фундаментальный коэффициент будет равен не 3/2 (отношение между промежутками во вспышках, посылаемых Борисом, и прохмежутками в их приеме Арнольдом), а просто 3 (рис. 20). Тогда один час по часам Бориса, прошедший между его встречами, станет тремя часами для Арнольда, а один час Вадима - всего третью часа, т. е. 20 мин, по часам Арнольда. Значит, согласно нашему прежнему рассуждению, по часам Арнольда прошло 3 час 20 мин между его встречами с Борисом и Вадимом. Если Арнольд отправляет второй радиолокационный импульс в 12 час 20мин дня (через 20 мин после того, как мимо него пролетел Борис), то в силу отношения 3/1 этот импульс достигнет Бориса через 60 мин после первой встречи - в 1 час дня по часам Бориса. Снова пользуясь соотношением 3/1, получим, что посланный в тот момент обратный сигнал придет к Арнольду в 3 час дня по его часам - через 160 мин после того, как был отправлен второй сигнал Арнольда. Значит, решит Арнольд, расстояние до второй встречи составляет 80 световых минут, а момент ее лежит посередине между 12 час 20 мин и 3 час дня - т. е. это 1 час 40 мин дня. Таким образом, за 100 мин по времени Арнольда Борис покрыл расстояние в 80 световых минут; это дает скорость, равную 4/5 скорости света - как раз 240 000 км/сек.
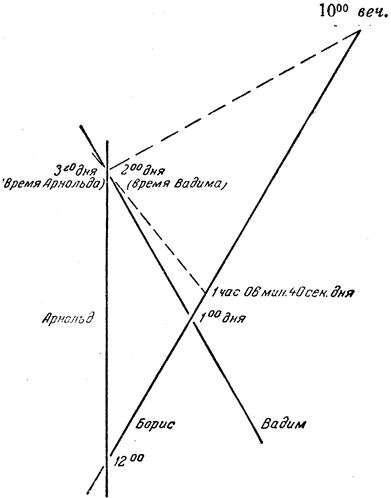
Рис. 20. Борис измеряет скорость Вадима (отношение интервалов 3:1)
При таком способе измерения скорость Бориса всегда будет меньше скорости света, Как мы увидим дальше, она вообще не может превзойти скорость света.
Что можно сказать о скорости Вадима относительно Бориса? Обыденная жизнь подсказывает нам привычную процедуру - скорости предметов можно просто складывать. Когда мимо нас проходит со скоростью 80 км/час поезд, а в нем вперед по направлению движения идет человек со скоростью 4 км/час, то скорость этого человека относительно нас составит 84 км/час. Но если мы станем вести расчет по этому примитивному способу и учтем, что скорость Вадима относительно Арнольда равна скорости Бориса, но направлена противоположно ей, а скорость Бориса составляет 4/5 скорости света, то получится, что Вадим движется относительно Бориса со скоростью, равной 8/5 световой, в явном противоречии с высказанным выше утверждением.
Однако не будем спешить с выводами. Только что мы разработали превосходный способ определения скоростей посредством той самой радиолокационной методики, которая применяется в действительности. Разве нельзя воспользоваться этим же способом, чтобы непосредственно найти скорость Вадима относительно Бориса в нашем примере? Пусть Борис решил определить, на каком расстоянии от него произошла встреча Арнольда с Вадимом. Пользуясь радиолокатором, он должен отправить импульс немного спустя после того, как Вадим пролетел мимо него - ведь свет движется быстрее Вадима, - а затем дождаться отраженного сигнала. При обсуждавшемся только что случае быстрого движения Вадим и Арнольд встретились через 200 мин (по часам Арнольда) после того, как Борис пролетел мимо Арнольда. Когда Борис должен послать свой радиоимпульс, чтобы он дошел до Арнольда именно в этот момент?
Так как отношение между интервалом при передаче к интервалу при приеме равняется теперь трем, то Борис должен по своим часам отправить сигнал через одну треть от 200 мин, т. е. через 1 час 06 мин 40 сек после того, как он миновал Арнольда (рис. 20), или через 6 мин 40 сек после того, как просигналил Вадим, находясь рядом с ним. Радиолокационный им пульс вернется к Борису за время, втрое большее, чем промежуток между встречами Арнольда с Борисом и с Вадимом, измеренный по часам Арнольда. Три раза по 3 час 20 мин дает 10 час, так что Борис примет ответный сигнал в 10 час вечера - через 8 час 53 мин 20 сек после отправления своего сигнала. Значит, расстояние до места встречи Арнольда с Вадимом по измерению Бориса равно 4 световым часам 26 световым минутам и 40 световым секундам. Момент этой встречи по часам Бориса лежит посередине между отправлением и приемом сигналов, а сигнал, принятый им, пришел через 4 час 33 мин 20 сек после того, как он повстречался с Вадимом. Значит, по данным Бориса Вадим прошел 4 световых часа 26 световых минут - 40 световых секунд за 4 час 33 мин 20 сек. Это дает скорость, близкую к скорости света, а именно около 97,5% ее, но не больше скорости света. Таким образом, складывая две скорости, каждая из которых равна 80% скорости света, мы получили лишь 97,5% скорости света.
Продолжая эти рассуждения, мы могли бы показать, что складывая любое число скоростей, каждая из которых меньше чем скорость света, мы никогда не сможем получить скорость, равную или превышающую скорость света - суммарная скорость всегда будет меньше ее. Отсюда следует, конечно, что сложение больших скоростей - вовсе не такое простое дело, как сложение малых, но этот вывод получился как раз в результате установления разумного способа измерения интервалов времени, расстояний и определения скоростей. Значит, скорость света оказалась у нас чем-то вроде радуги - как бы мы ни старались приблизиться к ней, мы никогда не сможем до нее достать.
Этот вывод представляется совершенно очевидным следствием наших предположений, если взглянуть на него с другой стороны. Когда наблюдатель движется медленнее света, отправленный им световой луч опережает его - с этим должен согласиться любой наблюдатель. Как бы ни двигался этот другой наблюдатель, излучатель света для него всегда летит медленнее самого света. А раз скорость света одна и та же для всех наблюдателей, то и его скорость по отношению к любому наблюдателю будет меньше, чем скорость света.
Взаимосвязь между k и υ
Для того чтобы распространить проделанные расчеты на самый общий случай, мы примем отношение интервалов равным k и предположим, что Арнольд посылает свой сигнал через время Т после того, как он и Борис пролетели друг мимо друга; момент встречи они оба для удобства выбирают в качестве начала отсчета времени. Борис примет тогда этот сигнал в момент времени kT, а его ответ дойдет до Арнольда в момент k•kT=k2T. Значит, Арнольд найдет, что промежуток времени между отправлением и приемом обратного сигнала равен (k2-1)T, так что расстояние от Арнольда до Бориса, когда последний посылал ответный сигнал, равно 1/2(k2-1)T. Кроме того, поскольку скорость света во всех направлениях одна и та же (и равна единице), то момент отправления Борисом ответного сигнала по определению Арнольда приходится на середину промежутка времени между отправлением прямого сигнала и приходом ответного, т. е. это 1/2(k2+l)T. Между моментом 0 и этим моментом Борис удалился из непосредственных окрестностей Арнольда на расстояние 1/2(k2-1)T. Поэтому скорость Бориса равна отношению этих двух величин, т. е.
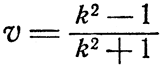
Отметим, что скорость υ здесь просто безразмерное число. Это естественное следствие того, что мы приравняли скорость света единице. Заметим также, что при k=l (интервалы одинаковы) мы получим состояние относительного покоя: υ=0; а замена k на 1/k лишь меняет знак скорости υ на обратный в согласии с выводами, сделанными в гл. 8. Наконец, при всех значениях k скорость лежит между -1 (приближение со скоростью света) и +1 (удаление со скоростью света). При υ=+1 это - прямое следствие нашего метода измерения, ибо иначе радиолокационный импульс не мог бы настичь Бориса; замена же k на обратную величину дает υ=-1. Решая уравнение (1) относительно k, получим
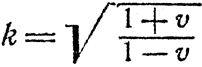
Связь между vυ и k проиллюстрирована также в табл. 5, где приведены и значения скорости в обычных единицах - км/сек.
| k | 1 | 1,001 | 1,1 | 1,5 | 3 | 10 | 100 |
|---|---|---|---|---|---|---|---|
| υ | 0 | 0,001 | 0,095 | 0,385 | 0,8 | 0,98 | 0,9998 |
| υ, км/сек | 0 | 300 | 28 500 | 115 500 | 240 000 | 294 000 | 299 940 |
Сложение скоростей
Перейдем теперь к сложению скоростей. Рассмотрим трех наблюдателей - Арнольда, Бориса и Давида, причем отношение интервалов при передаче к интервалам при приеме равно k для Арнольда и Бориса и k1 для Бориса и Давида, и предположим, что с точки зрения Арнольда Давид находится позади Бориса (рис. 21). Сигналы, отправленные Арнольдом с промежутком T, Борис примет с промежутком kT. Если при получении сигналов от Арнольда Борис будет также отправлять свои сигналы (очевидно, с промежутками kT), то Давид получит их с промежутками kk1T одновременно с сигналами от Арнольда. Значит, отношение интервалов для Арнольда и Давида равно kk1 или, говоря иначе, значения k перемножаются в цепочке наблюдателей. Это и есть фундаментальное правило сложения скоростей, дающее при малых скоростях всем знакомое обычное сложение. Отметим, что какие бы числа ни получались при перемножении величин k, скорость, соответствующая всему произведению (обоим крайним наблюдателям в цепочке), всегда меньше скорости света [см. формулу (1)].
Для того чтобы перевести закон умножения отношений на язык скоростей, обозначим через υ скорость пары Арнольд - Борис, через ω - пары Борис- Давид, а через w - пары Арнольд-Давид. Мы получим тогда:
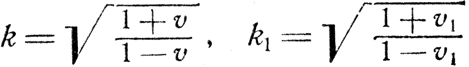
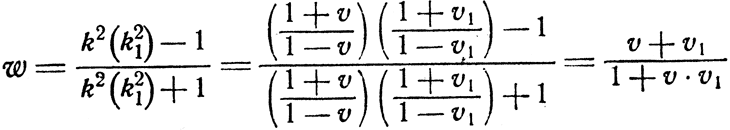
Отсюда сразу видно, что при малых υ и υ1 их сумма равна ω; в то же время любые υ и υ1 не превышающие единицы, дают ω, также не превышающую единицу. Этот результат в точности подтверждает те выводы, которые мы уже получили в частных примерах.
Собственная скорость
Существует и другой способ определения скорости; эта новая скорость не так близка к обычно используемому понятию (путь, пройденный за единицу времени), но все же оказывается полезной.
Пользуясь радиолокатором, Арнольд применяет, вероятно, единственно возможный метод определения расстояния до места встречи Бориса и Вадима. Однако для определения времени этой встречи он вычислял среднее из времен излучения и возвращения назад своего радиолокационного сигнала, хотя это не единственный способ определения времени. Вместо этого он мог бы посмотреть на часы Бориса и взять отношение того расстояния, которое Борис пролетел согласно измерению Арнольда, ко времени, которое потребовалось для того, чтобы покрыть это расстояние, по часам самого Бориса. Полученная таким образом "гибридная" величина называется собственной скоростью. Мы говорим "собственная" потому, что делим расстояние на время, в котором живет Борис - его собственное время. По часам Бориса прошло 60 мин с того момента, как он миновал Арнольда и пока не повстречал Вадима. За это собственное время он прошел 25 световых минут, и его собственная скорость поэтому равна 5/12 вместо 5/13 - значения, полученного раньше для его обычной скорости. Если теперь перейти к рассмотренному позднее более быстрому движению, когда отношение интервалов передачи и приема для Бориса и Арнольда составляло 3/1, то вспомним, что при встрече с Вадимом расстояние Бориса от Арнольда составляло 80 световых минут. Кроме того, по часам Бориса к тому времени прошел 1 час с момента встречи с Арнольдом, так что его собственная скорость в этом случае равна 4/3. Значит, собственная скорость объекта может быть больше единицы. Ясно, что она может расти неограниченно, и собственная скорость света, определенная таким же образом, будет равна бесконечности - вывод, который можно сразу же сделать из проведенных выше рассуждений.
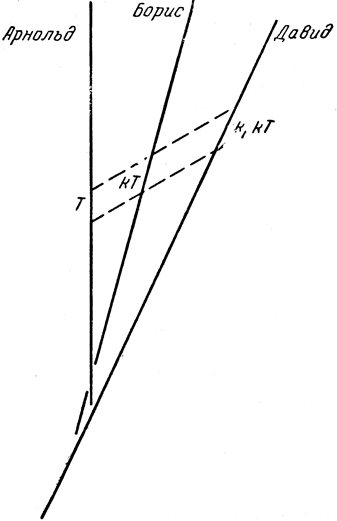
Рис. 21. Комбинирование коэффициентов k
Для многих вычислений в теории относительности удобнее использовать собственную, а не обычную скорость. Дело в том, что для получения обычной скорости мы делим длину пути, которую разные наблюдатели считают разной, на время, которое также будет разным для разных наблюдателей. Напротив, при вычислении собственной скорости мы хотя и берем прежний путь, измеряемый по-разному разными наблюдателями, но уже по крайней мере время здесь - это собственное время, измеренное самим "путешествующим" наблюдателем, а потому это нечто такое, с чем согласится любой. Кто бы ни поглядел со стороны на часы Бориса в два определенных момента, соответствующие событиям, происшедшим в жизни самого Бориса, - он увидит на них одно и то же время для каждого события, а значит, получит одинаковый интервал времени между парами событий.
Особый характер света
Из наших рассуждений следует еще один вывод. Мы уже видели, что, увеличивая отношение интервала приема к интервалу передачи между Борисом и Арнольдом с 3/2 до 3, мы приходим к возрастанию расхождения в величине времени, прошедшего между встречей Арнольда с Борисом и встречей Арнольда с Вадимом, если это время определяется по часам Арнольда и по часам Бориса или Вадима. Мы принимали, что в обоих случаях результат комбинированного измерения Бориса и Вадима был равен 2 час, тогда как результат измерения Арнольда увеличился с 2 час 10 мин до 3 час 20 мин. Очевидно, чем больше взять отношение интервалов, тем длительнее станет промежуток времени, измеренный Арнольдом. Мы можем поступить и наоборот: сохранять интервал, измеряемый Арнольдом, неизменным, и тогда при увеличении отношения промежуток времени, измеренный Борисом и Вадимом, будет убывать. Чем ближе подходит к скорости света скорость Бориса и Вадима с точки зрения Арнольда, тем труднее догонять их световым сигналам, и поэтому отношение интервала при приеме к интервалу при передаче возросло в наших примерах с 3/2 до 3 и станет возрастать далее до бесконечности, если рассматривать все большие скорости. Значит, чтобы сделать время, прошедшее с точки зрения Арнольда между его встречей с Борисом и встречей с Вадимом, постоянным, одинаковым для всех случаев, нам следует уменьшать сроки, измеренные между первой и последней встречами совместно Борисом и Вадимом. Если мы перейдем к пределу и заставим Бориса с Вадимом путешествовать верхом на световых волнах, то по их часам между этими встречами вообще не пройдет никакого времени.
Нельзя представить себе реальных людей, летающих со скоростью света, ибо, как мы увидели это раньше, не существует способа придать им такую скорость; однако можно подумать о самом свете. Можно представить себе в точке встречи Бориса с Вадимом зеркало, от которого отражается луч, посланный Арнольдом и возвращающийся назад к Арнольду. Если бы теперь этот световой луч нес с собой часы (сама по себе эта идея бессмысленна, но можно построить цепочку случаев, в пределе приближающихся к этому), то на таких часах не оказалось бы зарегистрированным никакого промежутка времени между уходом от Арнольда и возвращением к нему (сумма времени, затраченного лучом на путь от Арнольда до зеркала, а затем от зеркала обратно к Арнольду). Это можно выразить и по-другому, сказав, что свет просто не стареет, что для света время не течет. Это открытие несколько проясняет факт исключительного и универсального характера света. Свет не может измениться после того, как он был испущен, - ведь он не стареет, а значит, должен всегда оставаться одним и тем же (Здесь речь идет только о поведении света в пустоте (вакууме). В материальных средах (вода, стекло и пр.) свет распространяется со скоростью, не равной 300 000 км/сек - его скорость в них нередко бывает много меньше, так что для такой среды полученные выводы неприменимы. - Прим. перев).
|
ПОИСК:
|