10. Координаты и преобразование Лоренца

До сих пор при выводе всех следствий из принципа относительности Эйнштейна мы пользовались коэффициентом k. Мы уже пришли к новым представлениям о природе времени, и, конечно, анализ с использованием коэффициента k мог бы еще успешно использоваться в дальнейшем, особенно при выводе тех следствий принципа относительности, которые могут непосредственно наблюдаться, а потому должны послужить наилучшим его подтверждением. Но, с другой стороны, в написанных до сих пор руководствах мы всегда имеем дело с координатами и с преобразованиями координат. Такой подход, конечно, совершенно равнозначен нашему, но было бы очень полезно и нам вступить в контакт с этим более обычным математическим подходом. Вот почему эта глава будет более математической по сравнению как с предыдущими, так и с последующими, но мы надеемся, что это окажется полезным - в особенности для тех читателей, которые уже раньше кое-что знали о теории относительности.

Координаты и их роль

Математик пользуется координатами для того,чтобы описать положение геометрической точки; возможно, что на примере этого метода лучше всего разобраться в смысле и значении координат. Проще всего тот случай, когда мы имеем дело с плоскостью, например с листом бумаги, классной доской или полом комнаты. Тогда положение любой точки на этой плоскости можно определить, задав расстояния от нее по перпендикулярам до двух прямых, расположенных под прямым углом друг к другу - двух координатных осей. Обыкновенно одну координату называют х, а другую у. Та линия, на которой у равняется нулю, называется "осью х", а та, на которой х равняется нулю, - "осью у". Если эти две оси заданы, то при указании пары чисел х и у можно сразу найти на плоскости точку, соответствующую этой паре чисел; обратно, если указана какая-либо точка на плоскости, то достаточно просто измерить расстояния от нее до осей по перпендикулярам к ним, чтобы получить ее координаты. Мы видим, что это очень простой и быстрый способ указания мест точек на плоскости; поэтому он так часто и употребляется.

Здесь имеется одно затруднение, впрочем, неизбежное: координатные оси могут быть выбраны произвольно. Каждая пара осей так же хороша, как и любая другая. Что же произойдет, если изменить координатные оси? Изменять их можно двумя разными способами. Во-первых, и это проще всего, можно переместить их, но так, чтобы они остались параллельными прежним осям - иначе говоря, направление новых осей будет точно тем же, что и направление старых, только пересекаться они будут уже в новой точке. Если взять какую-то точку на плоскости и обозначить ее новые координаты через х' и у', то ясно, что они будут равны старым ее координатам просто плюс какие- то два (для каждой координаты свое) числа. Мы получаем имя и отчество каждой точки на плоскости в новых координатах, взяв ее старое имя (х) и отчество (у) и попросту прибавив одно число к имени, а другое - к отчеству. Эти добавочные числа будут теми же самыми, где бы наша точка не находилась, потому что они - просто координаты старого начала (точки пересечения старых осей) в новой системе координат.

Гораздо больше содержания (и притом очень для нас здесь существенного) в другом выборе новых координат - когда вместо того, чтобы произвести параллельный перенос осей, мы повернем нашу пару осей на какой-то угол. Пусть даже мы сохранили старое начало координат, ограничившись таким чистым поворотом, - мы все равно видим, что связь между старыми координатами и новыми (их преобразование) будет уже не такой простой. Нам незачем входить в какие-то подробности, но сразу же ясно (и это главное), что новая координата х будет зависеть сразу как от старой координаты х, так и от старой координаты у; то же самое можно сказать и о новой координате у. Другими словами, при переходе к новым координатам мы берем комбинацию старых.

С таким усложнением мы знакомы из повседневной жизни. Глядя на дом, мы называем одну его сторону шириной, а другую - длиной, но если мы завернем за его угол и взглянем на него с другого места, то прежняя ширина может нам представиться длиной, и наоборот. Если же мы посмотрим по диагонали на сложно спланированное здание, то проекции его архитектурных комплексов могут перемешаться в наших глазах, и его новая ширина окажется какой-то комбинацией старой ширины и старой длины, которые мы видели с другого места. Вся суть здесь в том, что математики называют двумерностью плоскости. Чтобы указать положение точки на плоскости, необходимо два числа, и при повороте наших осей эти числа комбинируются друг с другом. Это свойство составляет важное отличие координат от других величин. Например, представим себе, что мы проектируем систему отопления дома, размещенную под полом. Для нас будет очень важно знать температуру в любой точке пола, и температура при расчете будет не менее важна, чем указание, на каком расстоянии от двух стен находится интересующая нас точка пола. Однако, хотя для описания каждой точки пола у нас было бы теперь три числа, а именно: ее расстояния от двух стен и температура в ней, - мы все-таки не назвали бы температуру третьим измерением. Этого мы бы не сделали именно потому, что не существует такого преобразования координат, имеющего хоть какой-нибудь смысл, при котором температура "перемешивалась" бы с двумя настоящими координатами.

Такая способность комбинироваться (перемешиваться) друг с другом и есть самое характерное свойство координат. При общем преобразовании координат мы и сдвигаем начало и поворачиваем оси координат, так что если в старой системе координат точка определялась парой чисел х и у, то в новой системе она будет определяться совершенно иной парой чисел х' и у'. Тем не менее между этими разными системами координат существует тесная связь. Возьмем две точки: х, у и х, у. В новой системе координаты первой точки будут х', у' а второй х', у'. Однако и в старой, и в новой системе одна величина останется без всякого изменения - это расстояние между взятыми точками. Иначе говоря, для этих четырех чисел, которые описывают положение двух точек, должна иметься такая комбинация (именно то, что мы называем расстоянием между этими точками), которая в точности одинакова как в старой, так и в новой системе координат. Величины такого сорта математики называют инвариантами, потому что они не варьируют, не изменяются при изменениях систем координат.

Поворот осей

Поскольку преобразование, сводящееся к параллельному сдвигу осей, весьма несложно, то мы можем пользоваться им, как захотим. Например, можно сперва перенести начало координат в одну из двух рассматриваемых нами точек - скажем, в х, у, - после чего приступить к повороту осей, оставляя начало в этой точке (в принципе на эти операции можно разложить любое наше преобразование). Чему же равно расстояние точки х, у от начала координат? Для того чтобы ответить на этот вопрос, следует просто применить теорему Пифагора: квадрат искомого расстояния равен х²+у². Если повернуть вокруг этого начала координатные оси, то расстояние точки от начала останется прежним; тем самым доказывается теорема, что при повороте координатных осей выражение х²+у² переходит само в себя. Его величина не изменяется ни в малейшей степени. Из этого мы заключаем, что плоскость двумерна, потому что, во-первых, для указания места точки на ней требуются две координаты; во-вторых, когда мы меняем координатные оси, эти две координаты комбинируются друг с другом; в-третьих, существует инвариант - такая конструкция, построенная из этих координат, которая не изменяется при преобразованиях. Рассмотрим пример: пусть оси (х', у') наклонены на 30° к осям (х, у). Тогда, вспомнив основы тригонометрии, мы получим из рис. 22 закон преобразования:

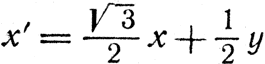
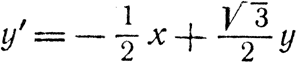
и наш инвариант действительно не изменяется:

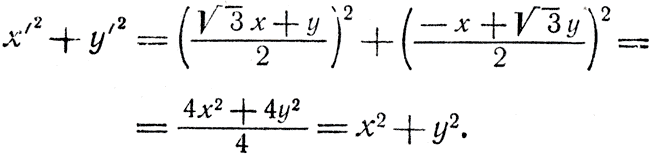
Мы говорим, что пространство, в котором мы живем, трехмерное, так как необходимы три координаты: длина, ширина и высота, или х, у и z, - для того, чтобы указать в нем положение всякой гочки. Положение точки определяется точно так же, как и в случае двух измерений. Для этого берутся три координатные оси, под прямым углом друг к другу, и расстояние по перпендикуляру от нашей точки до плоскости, в которой лежат оси х и у, называется координатой z, и т. д. (Такие системы координат, в которых оси прямолинейны и перпендикулярны друг другу, называются декартовыми; существуют еще сферические, цилиндрические и многие другие системы координат (например, такие, когда роль одной или нескольких координат играют угловые, а не линейные расстояния между точками). - Прим. перев)

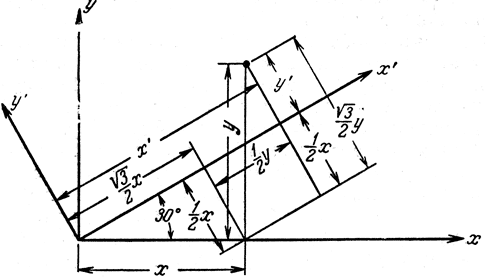
Рис. 22. Поворот координатных осей

Дело снова обстоит так, что имеются три числа, необходимые для указания точки, что эти числа комбинируются друг с другом, когда мы переходим к другой системе координат, и наконец, что существует инвариант (расстояние между точками), который не изменяется при преобразованиях координат. Мы имеем дело с двумя сортами преобразований координат - первым, почти тривиальным, когда только сдвигается начало координат, а к координатам всех точек добавляются три постоянных числа, и вторым, намного более сложным, когда оси поворачиваются так, что новые оси направлены косо по отношению к старым. Если, сохраняя в одной и той же точке начало, поворачивать таким образом координатные оси, то мы снова на основании теоремы Пифагора найдем, что величина х²+у²+z² остается неизменной. Существенно, что не меняется только одна эта величина - единственный инвариант, если допустить совершенно произвольные повороты осей.

Однако полезно еще немного остановиться на обсуждении этих преобразований. Предположим, что кто-то всегда направляет ось z по вертикали вверх; тогда он может позволить себе из всех преобразований лишь поворот осей х и у в горизонтальной плоскости. Неважно, как меняет он эти две оси - все равно координата z от этого не изменится. Значит, по мнению такого наблюдателя, в пространстве существует два инварианта - сама координата z и комбинация х²+у², не изменяющаяся при поворотах осей х и у в их плоскости. Все это звучит убедительно, пока он экспериментирует на достаточно малой площади, пока понятие вертикали остается совершенно строгим - именно, когда направления вертикали во всех точках параллельны. Однако если он захочет охватить сетью своих координат целый материк, то столкнется, конечно, с тем фактом, что направление по вертикали в одном месте не то же, что в другом, и нет разумных оснований для того, чтобы одна из осей - ось z - всегда была направлена по вертикали. Поэтому, как только он расширит свой кругозор, ему придется расширить и заколдованный ранее круг преобразований координат и рассматривать даже такие системы, в которых ось z направлена по наклонной. Когда это произойдет, он будет считать, что существуют уже не два его инварианта z и х²+у², а один x²+у²+z². До того как он пришел к такому заключению, он еще мог бы провозглашать: "Высота - это нечто совсем иное, чем ширина и длина, и никак не может случиться, чтобы она смешалась с ними; это вещи, не имеющие между собой ничего общего!". Однако, научившись ценить и наклонные оси, он позже скажет: "Конечно, все они одинаковые - и х, и у, и z. Ведь они же все перемешиваются, когда я наклоняю координатные оси, да к тому же существует всего один инвариант, построенный из всех трех".

Преобразование Лоренца

Как все это вписывается в теорию относительности? Вспомним, что путеводной звездой нам все время служил эйнштейновский принцип относительности, утверждающий, что все инерциальные наблюдатели равноправны. Именно этот принцип позволил нам сделать далеко идущие выводы о том, что происходит при больших скоростях (сравнимых со скоростью света). Самый важный из полученных нами выводов заключается в том, что физическое время - скорее индивидуальное, чем всеобщее, а результаты измерений времени, проделанных разными наблюдателями, не должны обязательно совпадать. Этот вывод был самым удивительным, он совершенно не соответствовал тому, что думали до Эйнштейна. На малых скоростях все времена совпадают, сливаясь во всеобщее время, и всякий, привыкший работать при малых скоростях, начинает думать, будто время - это инвариант. Все обстоит точно так же, как с тем наблюдателем, который экспериментировал на маленьком участке Земли, где направление вверх (вертикаль) кажется несомненным, и который мог поэтому вообразить, будто координата z - это инвариант. В гл. 8 мы уже показали, что дело обстоит иначе, что время становится другим, когда мы рассматриваем большие скорости, а значит, время нельзя считать инвариантом. Как же преобразуется время и как перейти от одного инерциального наблюдателя к другому? Эти преобразования можно уже получить с помощью нашего метода коэффициента k; они называются преобразованиями Лоренца (Лоренц получил свои преобразования, проводя теоретическое исследование законов электромагнетизма, и попытался с их помощью объяснить эксперимент Майкельсона - Морли. Ирландский физик Дж. Ф. Фитцджеральд утверждал, что отрицательного результата этого опыта следовало ожидать, если длина движущихся тел, измеренная покоящимся наблюдателем, подвергается сокращению в направлении движения. Преобразования Лоренца идеально согласуются с этой гипотезой. Эйнштейн вывел те же самые формулы преобразований, исходя, однако, из иных предпосылок. Вошло в обычай выводить это преобразование по методу, использованному Эйнштейном, и строить специальную теорию относительности, начиная с формул, связывающих пространственные и временную координаты двух наблюдателей, движущихся друг относительно друга равномерно и прямолинейно).

Пусть Арнольд пользуется координатами t и х, а Борис - координатами t' и х', так что положение Арнольда выражается как x=0, положение Бориса х'=0, а в момент встречи Арнольда и Бориса t=t'=0. Возьмем теперь событие, находящееся за Борисом с точки зрения Арнольда (рис. 23). Арнольд посылает радиолокационный импульс в момент t-х и получает его отражение в момент t+х, так что вычисленные им из этих чисел координаты t и х события равны именно t их. Подобным же образом Борис посылает сигнал в момент t'-х', а принимает его отражение в t'+x'. Пусть, однако, Борис посылает свой сигнал, когда сигнал Арнольда проходит мимо него, получая обратно отраженный, когда мимо проходит и отраженный сигнал Арнольда. Значит,

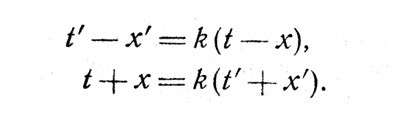
Отсюда сразу же следует, что

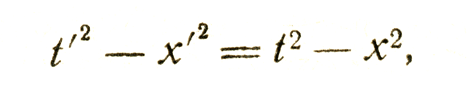
и после простых вычислений

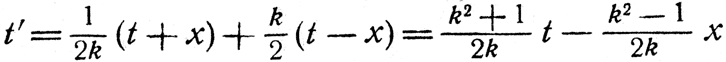
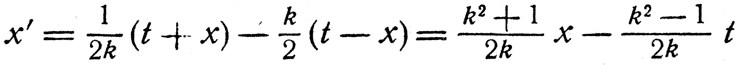
Выражая с помощью соотношения (2) на стр. 101 k через υ, получим формулы преобразований Лоренца:

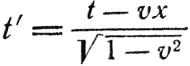
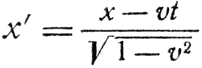
О чем мы можем заключить, взглянув на эти несложные формулы? Во-первых, для определения любой новой координаты каждого события требуется знать, чему равны обе старые координаты этого события. Пожелав узнать, чему равна временная координата определенного события для Бориса, нам нужно подставить в уравнение для t' (8) и пространственную, и временную координаты события с точки зрения Арнольда - и наоборот, так что при преобразованиях координаты t их комбинируются друг с другом. Во-вторых, из формулы (6) видно, что для такого преобразования существует инвариант, и этот инвариант удивительно похож на тот, который был у нас в двумерном случае (на плоскости), только квадраты в нем вычитаются, вместо того чтобы складываться. Мы видим, что в отношении событий на схемах Арнольда и Бориса справедливы те же рассуждения, благодаря которым мы должны были сказать, что плоскость двумерна. Чтобы определить положение события, нам потребовалось два числа: t и х; они комбинируются между собой, когда мы производим преобразование от точки зрения Арнольда к точке зрения Бориса; имеется и инвариант, построенный из них. Значит, это пространство Арнольда и Бориса следует назвать двумерным пространством, одним из измерений которого является время.

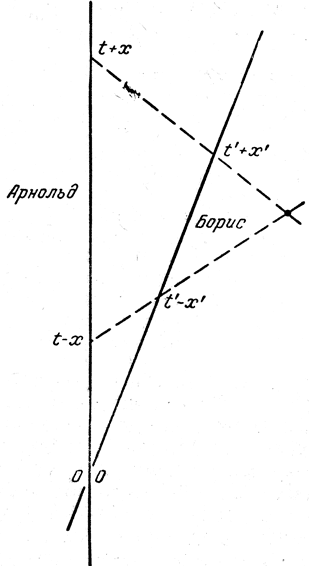
Рис. 23. Преобразование Лоренца

Чтобы разобраться в поведении остальных пространственных координат у, z и у', z', рассмотрим световой луч, испущенный событием, координаты которого в системе Арнольда равны а в системе Бориса - t₀, х₀. Поскольку свет распространяется со скоростью, равной единице, движение этого луча Арнольд опишет уравнением

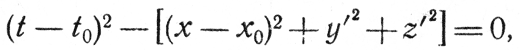
где квадратные скобки содержат квадрат расстояния от источника света. Борис запишет подобным же образом

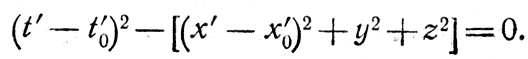
Однако

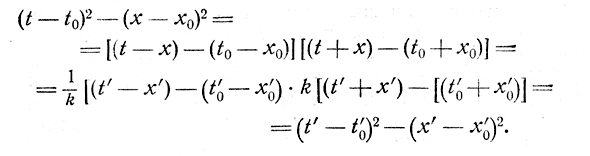
Поэтому из уравнений (9) и (10) следует, что

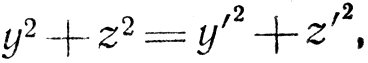
а так как подобную вспышку можно себе представить для любого события, то формула (12) должна выполняться всегда. Кроме того, заметив, что направления у и z симметричны относительно направления движения наблюдателей, мы придем поэтому к двум последним формулам преобразования Лоренца

Четыре измерения

Рассмотрим вместе формулы (6) и (13). Прежде всего мы вспоминаем пространство, в котором три пространственные координаты х, у и z перемешиваются друг с другом при поворотах. Скорость же при переходе от Арнольда к Борису перемешивает четвертую координату t с остальными тремя. Если взять все эти преобразования - и поворот, и переход к движению со скоростью Бориса - вместе, то мы придем к четырехмерному пространству х, у, z в том смысле, что для определения времени и места события требуется задать все эти четыре координаты. Кроме того, при поворотах осей либо при переходе к системе, движущейся с некоторой скоростью относительно предыдущей, все эти координаты комбинируются в новые. Наконец, существует и инвариант, а именно t²-х²-у²-z².

Такое использование "четырех измерений" часто ставит людей в тупик и просто пугает; они думают, будто физики и математики каким-то таинственным образом способны представить себе четырехмерный мир. Но это просто не соответствует действительности! Когда мы говорим о четырех измерениях, то не подразумеваем ничего, кроме того, что эти четыре величины - временная и пространственные координаты - ведут себя именно так, как только что говорилось, а значит, их можно все рассматривать как измерения в этом четырехмерном мире, точно так же, как пространственные измерения в обычном трехмерном мире. Конечно, в первый момент людей смущает, что время, прежде считавшееся инвариантом, вовсе таковым не оказалось; но ведь единственная причина того, что мы не представляли себе возможности комбинирования времени с другими координатами, - это непривычность таких больших скоростей, какие мы здесь рассмотрели. Когда скорость очень мала, то из преобразований Лоренца следует, что время не преобразуется. Однако при больших скоростях оно не остается по-прежнему неизменным!

Следствия из преобразований Лоренца

Теперь можно указать множество следствий, вытекающих из преобразований Лоренца - ведь все выводы из теории относительности являются просто результатом использования преобразований Лоренца.

Прежде всего это относительность одновременности. Из преобразований Лоренца сразу видно, что если два удаленных друг от друга события представляются одновременными Арнольду, то они уже не будут одновременными для Бориса. Раз эти события произошли далеко друг от друга, то хотя Арнольд и приписывает им обоим одну и ту же координату t, координаты х он дает им разные. Из формулы (8) тогда следует, что Борис должен будет приписать этим событиям разные значения временной координаты t. То, что один инерциальный наблюдатель воспринимает как происшедшее одновременно в двух пространственно разделенных точках, другой наблюдатель уже не будет считать одновременным. Это - новый пример индивидуальной природы времени, и в одной из следующих глав мы разберем это заново с помощью нашего метода коэффициентов k.

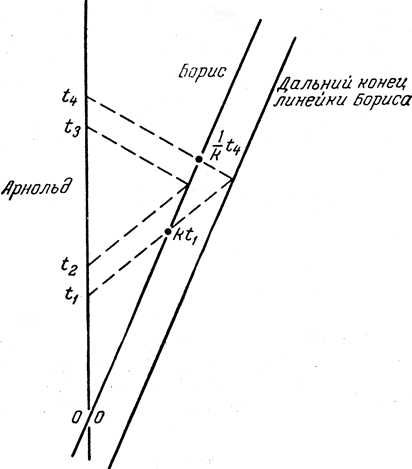
Рис. 24. Фитцджеральдово сокращение

Фитцджеральдово сокращение - так называется тот факт, что в координатах Арнольда длина линейки, которую Борис держит в направлении своего движения, будет меньше, чем длина этой же линейки по измерениям Бориса, Это непосредственно следует из преобразований Лоренца. Пусть координаты концов линейки в системе Бориса будут x'=0 и x'_*=L. Из формул (8) следует, что эти координаты в системе Арнольда будут равны соответственно

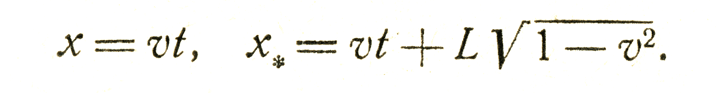
Если взять положения этих точек в один и тот же момент времени по Арнольду, то длина линейки, согласно измерениям Арнольда, будет равна всего лишь L√l-υ².

Этот же результат можно получить и по методу коэффициентов k. Чтобы измерить положение дальнего конца линейки, Арнольд пошлет сигнал в момент t₁, а отраженный сигнал придет к нему в момент t₄ (рис. 24), В момент t₂ он отправит сигнал Борису (координаты которого совпадают с координатами ближнего конца линейки) и получит назад отраженный сигнал в момент t₃. Так как Арнольда интересует разность расстояний до ближнего и дальнего концов линейки в один и тот же момент времени по его, Арнольда, часам, то ему следует так подобрать времена посылки сигналов, чтобы удовлетворялось равенство

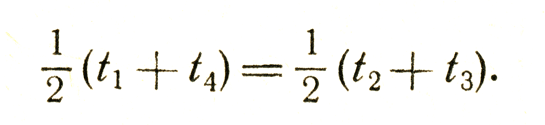
При этом, как обычно,

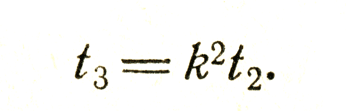
Кроме того, сигнал, отправленный в момент t₁, придет к Борису в момент kt₁ а сигнал, который Арнольд получит в момент t₄, пройдет мимо Бориса в момент t₄/k. Борис определяет длину линейки (измеряя ее) как L, так что промежуток времени между отправлением сигнала и его возвращением должен составить 2L; поэтому

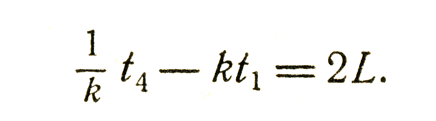
В системе Арнольда расстояние до дальнего конца линейки определяется как ¹/₂(t₄-t₁), а до ближнего - как ¹/₂(t₃-t₂), так что по измерению Арнольда длина линейки равна

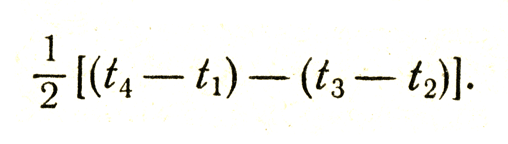
Если учесть зцесь формулы (14), (15) и (16), то мы получим

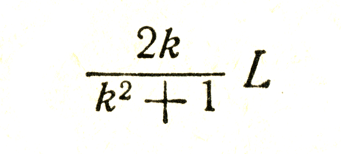
или, учитывая (2),

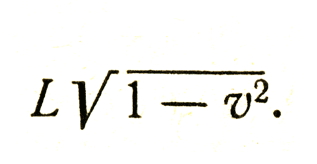
Следует подчеркнуть, что главное в рассуждениях Арнольда о сравнении расстояний до ближнего и дальнего концов линейки - это требование одновременности фиксации обоих расстояний по часам Арнольда. Видит же Арнольд вовсе не это! Если бы он сделал мгновенный снимок, то изображение Дальнего конца линейки относилось бы на нем к более раннему моменту, чем изображение ближнего конца, потому что свету приходится проходить различные пути от разных концов линейки (рис. 25). Если мы потребуем, чтобы отраженные сигналы вернулись в один и тот же момент t₃, то для этого необходимо послать радиолокационные импульсы в разные моменты t₁ и t₂, и они дойдут до Бориса соответственно в моменты kt₁ и kt₂. Теперь k(t₂-t₁)= 2L по измерению Бориса, и Арнольд найдет, что длина линейки на глаз представляется равной

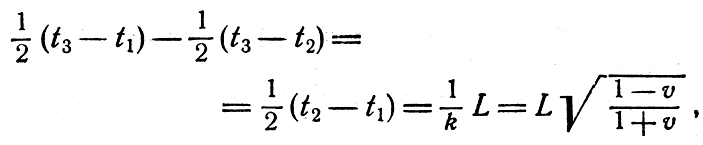
а это совсем иной результат, чем формула (19).

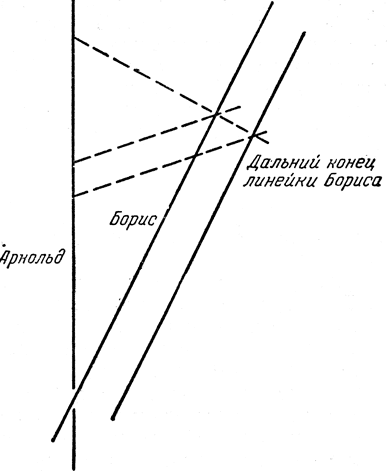
Рис. 25. Что видно на линейке Бориса

Чтобы лучше прочувствовать смысл соотношения (20), представим себе, чго на каждом конце линейки, которую держит Борис, горит огонек, и она скользит мимо другой линейки, которая покоится относительно Арнольда. Тогда те деления, которые Арнольд видит одновременно освещенными на своей линейке, и дают разность, определяемую формулой (20). Более глубокий и ученый ответ (19) Арнольд мог бы дать, если бы он сделал поправку на дополнительное время, которое нужно потратить свету для того, чтобы пройти длину линейки.

Аберрация света

Представим себе снова Арнольда и Бориса с их прежним выбором направления осей х и х'. Пусть летящий к Арнольду световой луч достигает его как раз в тот момент, когда мимо него пролетает Борис. Определяя направление, откуда пришел этот световой луч, Арнольд находит, что это направление составляет некоторый угол θ с его осью х. Борис обнаруживает луч в тот же момент, что и Арнольд, поскольку он как раз пролетает рядом с Арнольдом; спрашивается, какой угол θ' измерит он между направлением луча и своей осью х', которая, конечно, параллельна оси х системы Арнольда?

Предположим, что Арнольд и Борис поставили свои часы на нуль в момент встречи, а оси у и z своих систем (координаты в системе Бориса мы будем помечать штрихом) они направили так, чтобы на пути луча всегда было z=z'=0. Имея в виду, что, пока луч приближался к нашим наблюдателям, как t, так и t' были отрицательны, а также что скорость распространения света равна единице и для Арнольда, и для Бориса, мы получим

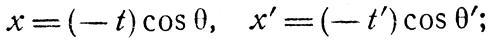
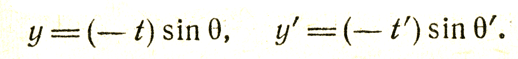
Подставив x' и t' из преобразований Лоренца (8) во вторую формулу (21) и разделив получившееся при этом соотношение для х и t на первую формулу (21), найдем

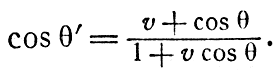
То же самое можно было бы получить, подставляя преобразования (8) и (13) в формулы (22).

Заметим прежде всего, что если θ=0 и cos θ=1, то cos θ'=1 и θ'=0, а если θ=180°, cos θ=-1, то cos θ'=-1 и θ'=180°. Несмотря на это совпадение, при промежуточных углах происходят значительные искажения. Для примера приведем в следующей таблице связь между θ и θ' при υ=0,8 (это соответствует k=3, т. е. уже рассматривавшемуся случаю):

Отметим, в частности, что вся область между θ=0 и θ=120°, составляющая для Арнольда три четверти всего неба, по мнению Бориса, втиснута в область от θ'=0° до θ'=60° и составляет только одну четверть неба.

В результате этого Борис обнаружит, что вселенная в направлении его движения сжата гораздо сильнее, по сравнению с картиной, которую видит в том же направлении Арнольд. Если Борис летит относительно Арнольда очень быстро, то большая часть неба Арнольда для него составляет лишь незначительную часть небосвода вокруг той точки, куда направлено его движение относительно Арнольда; остальная же часть неба Бориса будет для Арнольда сжата в маленький участок вокруг точки, противоположной той, к которой относительно него движется Борис. Это очень сильное искажение картины неба. Оно носит название аберрации света и исторически сыграло очень важную роль. Если бы Борис не двигался по инерции, а менял свою скорость, он обнаружил бы, что небо "переливается" вокруг него, и направления, в которых он видел бы звезды, все время менялись бы, не образуя постоянных углов друг с другом. Таким неинерциальным наблюдателем является наша Земля, обращающаяся вокруг Солнца - сегодня она летит по своей орбите в одном направлении со скоростью 30 км/сек, т. е. 1/10 000 скорости света, а через шесть месяцев она будет двигаться с той же скоростью в противоположном направлении, и соответственно этому изменятся углы между направлениями на разные звезды. Такое изменение углов было открыто еще в 1725 г. Джеймсом Брадлеем (Дж. Брадлей (1693-1762) - английский астроном, доказавший с помощью исключительно точных наблюдений в 1725-1727 гг., что явление аберрации не имеет ничего общего с годичным параллаксом (как предполагали до него), и в 1728 г. впервые объяснивший это явление. - Прим. перев), который тогда же и назвал его аберрацией света.

Первоначально аберрацию объясняли тем, что свет пролетает, словно пуля, сквозь телескоп и все время сохраняет свое направление движения, так что под действием движения телескопа места его попадания в объектив и окуляр оказываются сдвинутыми. Хотя это объяснение дает величину эффекта, мало отличающуюся от предсказываемой теорией относительности и наблюдающейся на опыте, оно в корне неправильно. Если бы мы наполнили телескоп водой, то, согласно этому старому объяснению, аберрация должна была бы увеличиться. Дело в том, что скорость света в воде иная, чем в воздухе, и свету понадобилось бы тогда больше времени, чтобы пройти от объектива до окуляра, так что телескоп сдвинулся бы за это время сильнее (прошел бы больший путь вместе с Землей в ее движении). Однако это на самом деле не так, правда, мы знаем об этом не из прямых наблюдений (Такого рода опыты производились и дали прямое подтверждение выводов, приведенных здесь Бонди (наблюдений английского астронома Эри в 1871 г.). - Прим. перев). Релятивистское объяснение, полученное с помощью формул преобразования Лоренца, очень хорошо согласуется с данными наблюдений, а кроме того, оно утверждает, что ничего бы не изменилось, если бы мы заполнили телескоп водой.

Открытие Брадлея сыграло важную историческую роль в том отношении, что оно послужило на первых порах прямой проверкой мысли Коперника о движении Земли вокруг Солнца. При этом обнаруживается, конечно, не сама скорость Земли (вещь ненаблюдаемая), но тот факт, что эта скорость изменяется, т. е. в разное время года положения звезд сдвинуты по-разному вследствие явления аберрации света. Это доказывает с полной достоверностью правильность коперниковской системы мира.