13. Масса возрастает

Исходным пунктом наших рассуждений была ньютоновская механика, которая и привела к принципу относительности Ньютона. Когда мы присовокупили к этому оптику, а тем самым представление о свете как о фундаментальном и исключительно своеобразном явлении, то мы пришли к теории относительности Эйнштейна. Затем, постоянно пользуясь методами световой сигнализации, мы изучили разнообразные следствия этой теории. В настоящей главе мы вернемся к механике и посмотрим, как следует изменить ньютоновскую механику, справедливую, как известно, при малых скоростях, для того чтобы она согласовалась с теорией относительности, рассматривающей и большие скорости.

Замедление хода времени

Сначала нам следует более внимательно подойти к понятию времени. Вернемся снова к нашим друзьям Арнольду и Борису, которые оба являются инерциаль-ными наблюдателями и находятся в одном и том же месте в 12 час дня по их часам, показывающим в этот момент одно и то же время. Относительно же друг друга они движутся с такой скоростью, что отношение между интервалами приема и передачи сигналов после их встречи равно 3/2. Значит, световой сигнал, отправленный Арнольдом через 40 мин по его часам после их встречи, достигнет Бориса, когда его часы отметят, что после встречи прошло 60 мин. Борис сразу же посылает ответный сигнал, который приходит к Арнольду через 90 мин после их встречи.

Если Арнольд захочет теперь определить тот момент, когда Борис посылал ему сигнал, то ему следует найти среднее время между 40 и 90 мин, что дает 65 мин. Хотя по часам Бориса этот момент был лишь на 60 мин позднее их встречи, по часам Арнольда он позднее встречи на 65 мин. Здесь важно не то, что Арнольд видит, как часы Бориса показывают 60 мин после их встречи, т. е. 1 час дня, когда на часах Арнольда 1 час 30 мин дня, а то, что для Арнольда существует лишь один способ учесть срок, потребовавшийся Свету для того, чтобы преодолеть его путь, а именно взять среднее между временем посылки и временем возвращения сигнала, в результате чего он получил 1 час 05 мин дня. Даже это время не согласуется с временем Бориса, и даже теперь, учтя поправку на время распространения света, он все равно обнаруживает, что часы Бориса отстают - ведь на них прошло всего 60 мин, когда по его, Арнольда, часам, минуло 65 мин. Естественно, что когда Борис движется быстрее, этот эффект становится заметнее.

Так, если мы снова, как делали это раньше, примем отношение интервалов передачи и приема равным 3/1, то найдем, что сигнал, достигший Бориса в 1 час дня по его часам, должен быть отправлен по часам Арнольда в 12 час 20 мин дня. Ответный сигнал должен вернуться к Арнольду в 3 час дня по его часам. Средним для этих двух моментов, т. е. для 12 час 20 мин и 15 час, будет 1 час 40 мин дня. Это момент по времени Арнольда, когда, согласно его определению, Борис ему отвечал, т. е. 1 час лия по часам Бориса. Итак, в системе Арнольда после учета времени, затраченного светом на весь путь, снова оказывается, что часы Бориса отстают - ведь они "прошли" всего 60 мин за 100 мин (от 12 час дня до 1 час 40 мин) по часам Арнольда. Это и есть замедление времени или замедление хода часов, оказавшееся во втором случае, которого мы будем продолжать придерживаться до конца этой главы, равным отношению 100/60, или 5/3.

Пусть теперь у Бориса есть линейка с метровыми делениями, которую он держит под прямым углом к направлению, в каком он видит Арнольда; пусть такая линейка есть и у Арнольда, и держит он ее параллельно линейке Бориса, т. е. тоже под прямым углом к направлению, в каком он видит Бориса. Тогда 1 м на линейке Арнольда выглядит так же, как 1 м на линейке Бориса, и наоборот, потому что когда Арнольд продвинется на 1 м вдоль своей линейки, т. е. перпендикулярно направлению Бориса, то напротив него окажется очередная метровая отметка на линейке Бориса. Значит, нет никакого труда переводить друг в друга расстояния, измеренные вдоль этих линеек - они просто равны друг другу.

Пусть теперь у Бориса вдоль его линейки движется частица со скоростью, которая, по измерениям Бориса, равна 60 км/час. Какой будет эта скорость для Арнольда? За выбранный промежуток времени по часам Бориса частица пройдет некоторое расстояние вдоль линейки Бориса, и Арнольд измерит точно тот же путь. Но тот промежуток времени, который по часам Бориса равен 60 мин, по часам Арнольда составит целых 100 мин!

В результате Арнольду покажется, что эта частица вместо того, чтобы двигаться со скоростью 60 км/час, будет делать всего 36 км/час, потому что те 60 мин, за которые эта частица по часам Бориса проходит 60 кму представляются Арнольду уже 100 мин, и пройти 60 км за 100 мин - это как раз означает движение со скоростью 36 км/час. Таким образом, если скорость движения вдоль линейки, измеряемую Борисом, принять за 100%, то скорость, найденная Арнольдом, будет равна 60%, так как длйны в рассматриваемом направлении одни и те же для обоих наблюдателей, а времена Арнольда и Бориса разные.

Возрастание массы

Однако в механике основной величиной является не скорость, а импульс. Полезно вспомнить, что это важное понятие ньютоновской механики представляет собой произведение скорости на массу и подчиняется закону сохранения. Для наших целей лучше определять величину импульса попроще. Можно, например, измерять импульс пули той наибольшей толщиной брони, которую она способна пробить. Предположим для простоты, что процесс пробивания брони пулей, ударяющейся в нее под прямым углом, целиком зависит лишь от импульса пули, и оставим в стороне такие усложняющие дело вещи, как форма пули и материал, из которого оиа сделана. Когда Борис стреляет определенным типом пули с определенной скоростью, то он может измерить ту наибольшую толщину брони, которую может пробить такая пуля. Если, с точки зрения Бориса, слой брони располагается перпендикулярно направлению полета пули, то и толщину пробитого слоя ему нужно измерять под прямым углом к поверхности этого слоя, и раз Арнольд смотрит на броню с торца, то результат его измерения толщины будет тот же, что и у Бориса.

Таким образом Арнольд может определить импульс пули Бориса и получить точно тот же результат, что и Борис. Напротив, измеряя скорость пули Бориса, движущейся в поперечном направлении, Арнольд получит всего 60% той величины скорости, которую отметил Борис. Значит, для того, чтобы получить требуемое значение импульса - то же, какое получил Борис, - Арнольд должен принять, что масса пули равна для него 5/3 массы, которую измерил Борис. Очевидно, это возрастание массы связано с замедлением времени, которое, в свою очередь, вызвано движением Бориса относительно Арнольда с данной скоростью. Значит, скорость движения Бориса привела, с точки зрения Арнольда, к увеличению массы пули Бориса. Благодаря этому эффекту увеличатся массы всех предметов, принадлежащих Борису, - ведь все их можно было бы исследовать на манер пуль, либо просто мы могли бы воспользоваться пулями для того, чтобы промерить все массы у Бориса.

Такой рост массы, т. е. инертности, нетрудно связать с другим фактом. С точки зрения Арнольда, если Борис движется по отношению к нему, то и сам Борис и все сопутствующие ему предметы имеют значительную энергию движения (кинетическую энергию). Разделив эту энергию на квадрат скорости света, мы придем к этой добавочной массе для каждого предмета Бориса. В наших единицах, когда скорость света равна единице, а скорости умеренны, так что справедлива механика Ньютона, эта добавочная масса точно равна ньютоновской кинетической энергии ¹/₂mυ², Поэтому разумно предположить, что в этом, как и в любом другом случае, теория относительности должна дать закон, распространенный на случаи больших скоростей и продолжающий законы Ньютона, и добавочная масса должна всегда равняться кинетической энергии, если взяты наши единицы. Чтобы перевести этот результат в привычные единицы, заметим, что энергия выражается через массу, длину и время как произведение массы на квадрат скорости. Поэтому в тех единицах, в которых скорость света равна не 1, а, скажем, с, добавочная масса будет равна кинетической энергии, деленной на с². Значит, наш вывод с одинаковым успехом можно выразить как возрастание массы со скоростью либо как наличие массы у энергии, и в этом втором случае добавочная масса пули рассматривается как инертность энергии ее движения.

Согласно первому подходу, масса, вместо того чтобы быть постоянной, как этого требовала теория Ньютона, в теории относительности превращается в нечто, зависящее от скорости, и легко понять, что эта масса делается сколь угодно большой, когда скорость стремится к скорости света. Впрочем, стоит отметить, что если взять "собственную скорость", которую мы ввели в гл. 9, то импульс получается при умножении ее на массу, уже не зависящую от скорости.

Когда частица движется со скоростью ненамного меньше скорости света, то ее масса намного превышает ее массу при покое - так называемую массу покоя. Если мы теперь передадим этой частице еще дополнительную энергию, чтобы она стала обладать большей пробивной силой, то мы сможем увеличить ее скорость лишь очень ненамного. Значит, энергия и пробивная сила частицы увеличиваются теперь за счет роста ее массы, и этот рост не имеет предела. Этот эффект наблюдается, он подробно изучен и в точности подтвержден, и, вероятно, это служит лучшей проверкой теории относительности.

Ускорение протонов

Для примера можно обсудить движение протонов в гигантском ускорителе Европейского центра ядерных исследований (ЦЕРН) в Мейрене, близ Женевы (Швейцария). Когда этот крупнейший ускоритель работает на полную мощность, он придает протонам энергию в 28 Бэв, выражаясь на языке физиков-ядерщиков (Электрон-вольт (эв) - это энергия, приобретаемая электроном при прохождении разности потенциалов в 1 в. Свечение телевизионной трубки (кинескопа) вызывается падением на ее экран электронов с энергией около 10000 эв. 1 Бэв - это 1000 000 000 эв, причем 6 Бэв равняются приблизительно 1 ватт-секунде - иначе говоря, каждый протон при всей своей мизерности (а в 1 г содержится 540 тысяч миллионов миллионов миллионов протонов) несет на выходе ЦЕРНовского ускорителя столько же энергии, сколько излучает ее в форме тепла и света в секунду одна маленькая электрическая лампочка в 5 вт). При такой энергии масса протона круглым счетом в 30 раз превышает его массу покоя. При этом он движется со скоростью, лишь на 160 км/сек, меньшей, чем скорость света (300 000 км/сек). Развивая этот пример, посмотрим, что происходит при ускорении протонов до такой скорости. Когда их энергия достигает 95% окончательной величины, то их скорость отличается от указанной конечной величины скорости лишь на ¹/₁₈₀₀₀ скорости света, т. е. на каких-нибудь 17 км/сек. Такая разность скоростей лишь ненамного больше скорости космических ракет, запускаемых в последнее время, и дальнейший этап ускорения поэтому относительно мало увеличивает скорость протонов. Главное значение его в увеличении их массы. Таким образом, на этом этапе добавление энергии почти не повышает скорости, но все же увеличивает пробойную силу за счет роста массы.

Когда мы отметили, что энергия этих частиц проявляет себя в виде массы, у нас должны были возникнуть следующие два вопроса:

1. Все ли формы энергии (такие, как свет и другие виды излучения, ядерная энергия и пр.) связаны с массой - или это качество связано лишь с энергией движения?

2. Пусть часть массы этих частиц соответствует энергии; соответствует ли тогда энергии и их масса покоя (та масса, которой они обладают в состоянии покоя)?

Что касается первого вопроса, то ясно, что с массой связана любая форма энергии, потому что самым характерным свойством энергии является ее способность переходить от объекта к объекту и из одной формы в другую (вспомним, например, такую цепь: химическая энергия угля - тепловая энергия пара на электростанции - электрическая энергия в проводах - энергия движения электропоезда). Если бы при переходе энергии из одной формы в другую масса изменялась (не сопровождала бы энергию), то не осталось бы камня на камне и от закона сохранения импульса, который выведен непосредственно из опыта и совершенно не зависит от внутренних изменений физической системы.

Представьте себе космический корабль с выключенными двигателями, летящий с постоянной скоростью. Его пассажиры используют энергию (запасенную, скажем, в аккумуляторах) то для приготовления пищи, то для работы стиральной машины. Согласно закону сохранения, эти внутренние превращения не могут изменить импульса системы в целом. Значит, если наш корабль покоился относительно одного инерциального наблюдателя до потребления в нем энергии, то он должен продолжать покоиться и после этого. Поэтому он не должен изменить своей скорости и относительно другого инерциального наблюдателя. Так как при этом не изменился и импульс, то масса должна оставаться постоянной и, следовательно, энергия должна обладать одной и той же массой, будь она заключена в аккумуляторе или имей она форму энергии движения стиральной машины (либо тепловой энергии кипятильника и пр.).

Уравнение Эйнштейна

Итак, каждая форма энергии обладает массой, которая равна, как и в случае энергии движения,

или

это и есть знаменитая формула Эйнштейна.

Сам Эйнштейн в одной из своих первых работ по теории относительности воспользовался другим способом для того, чтобы доказать наличие массы у энергии. Подумаем сначала, как заметить наличие массы, а не веса (вызванного условиями нашей жизни в поле силы тяжести Земли). В основном масса проявляет себя при действии силы, и в гл. 2 мы видели, как эта взаимосвязь массы и силы привела к понятию импульса. Важность понятия импульса следует из того, что оно применимо к системе в целом - независимо от того, что может происходить внутри этой системы (вспомним рассуждения о ребенке и коляске в гл. 2). В частности, если на систему не действуют никакие внешние силы, то ее импульс не может измениться, что бы ни происходило внутри этой системы. А раз импульс характеризует движение центра массы системы (ее центр тяжести), то, если этот центр первоначально находился в покое, он останется неподвижным и при всех переменах внутри системы, если снаружи на эту систему не действуют никакие силы. Сказанное представляет собой только более точное выражение той мысли, что невозможно поднять самого себя за волосы.

Приведем конкретный пример: пусть на гладком горизонтальном столе лежит длинный ящик (рис. 32). Если никто этот ящик не толкает, а его центр массы первоначально покоился, то этот центр будет оставаться неподвижным и впредь, что бы внутри ящика ни происходило. Это, однако, совсем не значит, что наружные стенки ящика никогда не будут двигаться! Если массы, находящиеся внутри ящика, сдвигаются, то изменяется и положение центра масс относительно его стенок - а коль скоро центр масс должен сохранять одно и то же положение, то сдвинется сам ящик. Предположим теперь, что в одном конце ящика лежит шар, а за ним - сильная сжатая пружина, которую в определенный момент отпускает часовой механизм. Когда часовой механизм сработал и пружина освободилась, она отбросила шар в другой конец ящика, где лежит какое-то вязкое вещество, останавливающее попавший в него шар. Что же произойдет с ящиком?

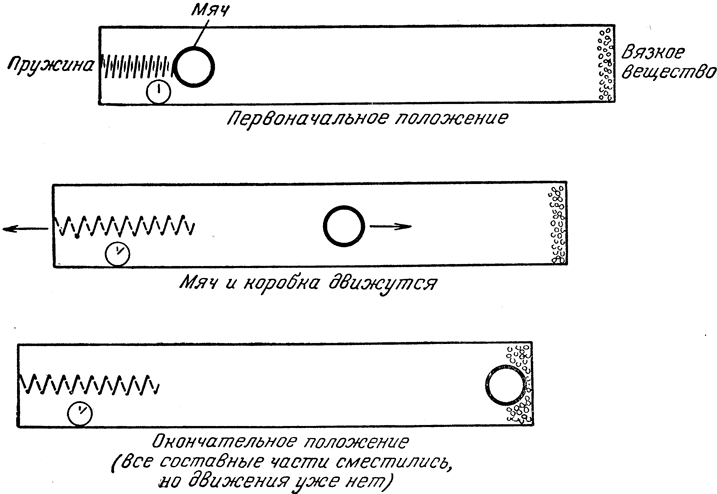
Рис. 32

Этот опыт подобен выстрелу из ружья. Происходит отдача - ящик начинает двигаться в направлении, противоположном направлению движения шара. Центр же системы в целом (ящик+шар), хотя и будет двигаться относительно ящика, останется неподвижным в пространстве, так что сам ящик станет двигаться в сторону, противоположную шару. Это движение будет продолжаться, пока шар не ударится в вязкое вещество у противоположной стенки, и это столкновение остановит ящик. Внешний наблюдатель лишь отметит, что ящик, неподвижный вначале, внезапно пришел в движение и так же неожиданно опять остановился; его окончательное положение при этом отличается от первоначального. Если он знаком с законом сохранения импульса, то признает, что центр масс всей системы в целом (ящик+его содержимое), покоившийся вначале, должен был оставаться неподвижным все время, потому что не действовало никакой внешней силы. Он должен будет поэтому прийти к выводу, что сдвиг ящика, заметный снаружи, вызван сдвигом масс внутри ящика (сдвиг шара). Если ему сообщить, на какое расстояние передвинулся шар и чему равна масса ящика, включая пружину и часовой механизм, то он может на основании величины сдвига самого ящика определить величину массы шара.

Этот пример - прямое следствие ньютоновской механики, и такие вычисления не затрудняли и самого Ньютона. Новый вывод, к которому пришел Эйнштейн, получается, если заменить в этом примере шар световой вспышкой. Необходимым свойством света в опыте Эйнштейна является тот факт, что свет оказывает давление на предметы. Падая на черную поверхность и поглощаясь на ней, он передает этой поверхности толчок; падая на зеркало и отражаясь от него, он передает ему двойной толчок. При любых практически достижимых интенсивностях света это давление весьма мало, но его существование непосредственно следует из максвелловской теории света, созданной еще за 40 лет до теории относительности, и его удается обнаружить, поставив опыт достаточно тонко.

Предположим, что мы взяли тот же ящик, но часовой механизм включает теперь в цепь батареи мощную лампу-вспышку, дающую короткий и очень сильный световой импульс (рис. 33). Пусть все стенки ящика светлые и хорошо отражающие свет, за исключением дальней (от лампы) стенки, окрашенной в черный цвет. Когда лампа включилась, она испускает свет во все стороны; если она ближе к одному концу ящика, то там отражается половина излучаемого лампой света, и на эту стенку действует давление, заставляющее ящик двигаться. Когда немного позднее свет дойдет до черного конца ящика (а ведь свету требуется некоторое время, чтобы пройти через длинный ящик!), то теперь свет здесь полностью поглотится, оказав на стенку такое давление, что ящик остановится.

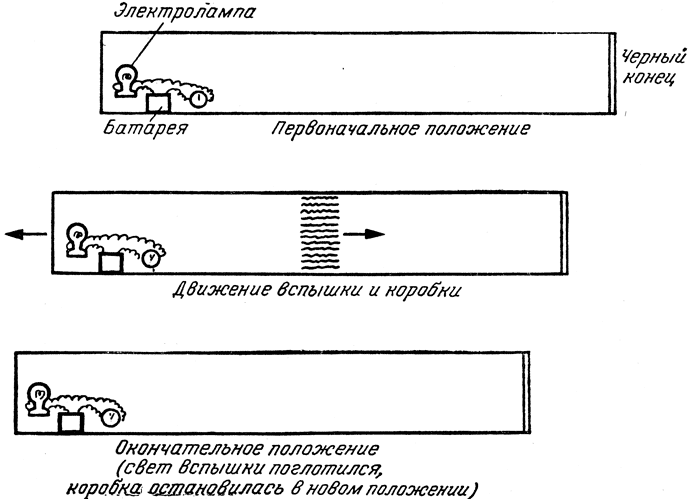
Рис. 33

Для внешнего наблюдения картина будет в принципе та же, что и в опыте с шаром. Ящик, бывший сначала неподвижным, внезапно приходит в движение, а потом останавливается в новом месте. Поэтому наблюдатель будет вынужден признать, что была перенесена масса из конца, где находится лампа, в зачерненный конец ящика, и величину этой массы он сможет сосчитать, зная сдвиг ящика. Из максвелловской теории света следует, что давление света на черную поверхность равно его интенсивности, деленной на скорость света. Учитывая это соотношение совместно с длительностью распространения света в ящике и продолжительностью вспышки, Эйнштейн обнаружил, что величина передвинутой массы равна энергии вспышки, деленной на квадрат скорости света.

Бесспорно, что энергия была здесь перемещена из конца ящика, где была лампа (и где первоначально эта энергия была запасена в батарее), в зачерненный конец, который нагрелся вследствие поглощения в нем света. Значит, этот мысленный эксперимент Эйнштейна показывает, что такой перенос энергии Е сопровождается переносом массы т, и эти две величины связаны друг с другом соотношением

Итак, энергия света, точно так же, как энергия движения, обладает массой. И снова, опираясь на этот вывод, мы можем, как и прежде, заключить, что всякая энергия должна обладать массой и должна быть связана с ней этим соотношением.

Переходя теперь к вопросу о том, соответствует ли энергии масса покоя, мы должны обратиться к ядерной физике. Все атомные ядра состоят из протонов и нейтронов. Масса сложного ядра меньше (иногда почти на 1%), чем сумма масс тех протонов и нейтронов, из которых оно состоит. Эта разность вызвана освобожденной (и излученной при этом) энергии, когда протоны и нейтроны, объединившись, составили это сложное ядро. В этом вся суть ядерной (атомной) энергии (атомные бомбы, атомные электростанции), и это же - доказательство эквивалентности массы и энергии. Таким образом, теория Эйнштейна не только объединила оптику и механику и не только выяснила смысл времени и пространства, но и объединила понятия массы и энергии.

Теория и наблюдения

На этом заканчивается наша короткая экскурсия в теорию относительности. Надеюсь, что мне удалось показать, как эта теория, казавшаяся на первых порах такой таинственной, на самом деле естественно и понятно вытекает из наших обычных представлений, являясь их продолжением в область больших скоростей. И то, что в ней непривычно для нас, непривычно только потому, что непривычны сами эти большие скорости. Но ведь нет никакого другого способа, который сделал бы мир больших скоростей таким простым и понятным для нас, кроме теории относительности Эйнштейна.

Однако главной целью любой научной теории является не просто простота и понятность - и не только обогащение нашего опыта и приведение разных наблюдений во взаимосвязь. Теория должна также соответствовать фактам, и в этом отношении можно смело сказать, нет, наверное, другого раздела физики, который был бы так проверен, изучен и опять проверен опытами, как теория относительности. Конечно, не был проверен на опыте ни один из тех мысленных экспериментов, на примере которых мы обсуждали эту теорию ради простоты, но точек соприкосновения этой теории с наблюдаемыми фактами настолько много, что и в тех примерах, о которых мы говорили, можно быть уверенными, что эта теория правильно описывает все случившиеся там происшествия.

Где бы ни проявлялись большие скорости - в ускорителях элементарных частиц или в оптике, - теория относительности неизменно выдерживала с честью опытную проверку. В ее лице к нашим представлениям о природе добавился такой раздел, которому, как мы верим, обязаны соответствовать все физические теории. И если нам удалось здесь показать, что эта теория не трудна и не таинственна, то можно сказать, что цель этой книги достигнута.