
8. К истории закона сохранения количества движения
Понятие количества движения как специальной механической величины, выражающейся произведением массы тела на скорость его движения, ввел Ньютон в "Математических началах натуральной философии". Количество движения связывалось вторым законом динамики с силой, изменение количества движения служило мерой силы.
С другой стороны, произведение массы на скорость рассматривалось как мера движения. Закон сохранения количества движения появился впервые именно при рассмотрении мер движения.
Первая формулировка принадлежит Декарту. В своем основном труде "Начала философии", вышедшем в 1644 г., Декарт развивает мысль о том, что Вселенная заполнена различными формами движущейся материи. Первопричиной движения он считает бога и дает следующую теологическую формулировку закона сохранения: "Бог - первопричина движения, он постоянно сохраняет в мире одинаковое его количество".
Декарт не дал математического выражения закона. Он лишь наметил первый шаг в следующей формулировке: "Когда одна частица материи движется вдвое скорее другой, а эта последняя вдвое по величине больше первой, то в меньшей столько же движения, сколько и в большей из частиц; и, что насколько движение одной частицы замедляется, настолько же движение какой-либо иной возрастает".
Далее смысл закона не проясняется, а, наоборот, запутывается. Лейбниц начал дискуссию о мере движения в работе с интересным названием "Краткое доказательство замечательного заблуждения Декарта и других в вопросе об одном законе природы, по которому, как они полагают, благодаря Господу сохраняется всегда одно и то же количество".
Лейбниц считает мерой движения не произведение mv, а произведение mv2. Он делает первый шаг к открытию закона сохранения энергии, но безнадежно запутывает вопрос о соотношении законов сохранения количества движения и энергии. Эта путаница бытовала более 100 лет и мешала прояснению закона сохранения энергии.
Развитие ньютоновской динамики привело к выяснению связи между законами динамики и законом сохранения количества движения.
Для одного тела 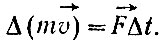 При отсутствии внешних сил
При отсутствии внешних сил 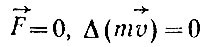 и сразу же следует сохранение количества движения:
и сразу же следует сохранение количества движения: 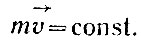 В случае постоянной массы
В случае постоянной массы 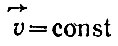 мы приходим к первому закону динамики.
мы приходим к первому закону динамики.
Рассматривая замкнутую систему взаимодействующих тел, можно написать
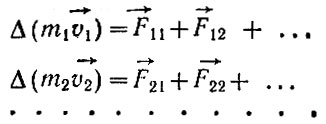
Суммируя правые и левые части и пользуясь третьим законом динамики, согласно которому 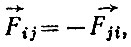 получаем
получаем
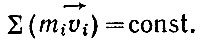
Методическое замечание. Рассмотренная связь между законами динамики и законом сохранения количества движения является результатом прямой логической линии развития механики. Здесь все строго, четко и ясно. Исторически это была не прямая, а очень сложная кривая. Естественно, что учащихся не следует вести по этой кривой. Важно подчеркнуть, что мы имеем дело не с выводом закона сохранения количества движения, как это часто представляют, а с выражением внутренней связи между законами динамики и законами сохранения.
В становлении закона сохранения количества движения важную роль сыграли его практические приложения. Изобретатели еще задолго до открытия закона использовали его в практике. Реактивное действие струи воды или газа было известно еще древним грекам. Однако для широкого использования реактивного движения в технике пришлось пройти очень долгий путь. Основоположник космических полетов К. Э. Циолковский разработал принципы практического использования реактивного движения только в 20-х годах нашего века, первые реактивные самолеты появились в конце Великой Отечественной войны, а первый искусственный спутник Земли запущен в 1957 г.
Следует иметь в виду, что вопрос о мерах движения, о связях законов сохранения с другими законами природы выяснен только в связи с развитием принципов теории относительности Эйнштейна и законов симметрии.
В настоящее время твердо установлено, что движение имеет две меры - скалярную и векторную. Скалярная мера - энергия, векторная - импульс. При этом обе эти меры являются составляющими единой меры - релятивистского тензора энергии - импульса.
Замена термина "количество движения" на "импульс" имеет глубокий физический смысл. Дело в том, что развитие физики показало, что количеством движения обладают не только частицы вещества, но и частицы электромагнитного излучения - фотоны. Для фотона мы не можем написать произведение 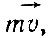 как для кусочка вещества. Фотон количественно определяется двумя соотношениями E=hv и E=mф·c2 отсюда
как для кусочка вещества. Фотон количественно определяется двумя соотношениями E=hv и E=mф·c2 отсюда 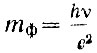 и импульс
и импульс 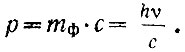
|
ПОИСК:
|