20. Световые волны

 ●249. Всегда ли применим закон обратных квадратов?

При больших размерах источника света нельзя пользоваться законом обратных квадратов для расчета освещенности поверхности. Однако можно мысленно разбить всю поверхность большого источника на столь малые участки, чтобы для каждого из них закон обратных квадратов был применим. Почему же закон неприменим для источника в целом?

 ●250. Пламя свечи - неиссякаемый источник энергии.

Энергия, излучаемая точечным источником, падающая в единицу времени на единицу поверхности, нормально расположенной к к лучам на расстоянии r от источника, равна

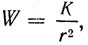
где К - энергия, получаемая в единицу времени той же поверхностью от того же источника, помещенного на единичном расстоянии. Следовательно, внутри самого пламени свечи, для которого r = 0, должно быть W = ∞ т. е. пламя свечи дает в единицу времени бесконечно большое количество энергии, что, конечно, неверно. В чем ошибка рассуждений?

 ●251^*. Может ли свеча дать бесконечно большую энергию?

Пусть в центре вогнутого сферического зеркала (в пределе в центре зеркальной сферы) помещена свеча. Лучи после отражения снова сойдутся в центре зеркала, но сила света действительного изображения свечи будет несколько меньше одной свечи, положим 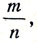, где m 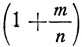свечи. Этот источник света дает действительное изображение с силой света 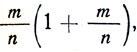так что общая сила света будет:

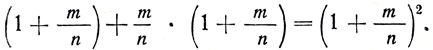
Повторяя те же рассуждения бесчисленное число раз, придем к заключению, что в центре зеркала находится источник света с общей силой 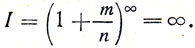Этот вывод явно противоречит теории и опыту. В чем ошибка рассуждений?

 ○252. Ближе - холоднее, дальше - теплее.

Чем ближе площадка к точечному источнику света инфракрасного излучения, тем больший поток энергии падает на нее. Зимой Земля ближе к Солнцу, чем летом. Однако зимой холоднее, чем летом. Как разрешить это противоречие?

 ●253. Экспозиция не зависит от расстояния.

Фотографируя некоторый предмет аппаратом, главное фокусное расстояние объектива которого равно 5 см, например с расстояния 10 м, делают экспозицию 0,01 сек. Если съемку того же предмета производят с расстояния 20 м, то экспозицию не меняют.

Но ведь с увеличением расстояния световой поток от предмета, падающий на фотопленку, уменьшается. Значит, надо было бы увеличивать экспозицию, чтобы получить снимок того же качества. Как разрешить противоречие?

 ○254. Яркость объемного источника света не зависит от расстояния.

Освещенность, которую дает электрическая лампа с матовой поверхностью стеклянного баллона, обратно пропорциональна квадрату расстояния до лампы. Однако, приближаясь или удаляясь от лампы, мы видим ее баллон одинаково ярким (случаи очень близкого приближения лампы к глазу и удаления ее "на бесконечность" исключаются). Как объяснить этот парадокс?

 ●255. Условия интерференции.

Если разность хода световых лучей равна nλ, где n - целое число, а λ - длина волны, то волны усиливают друг друга. В точках А и В (рис. 131) находятся когерентные источники света. От этих источников свет распространяется в вакууме и попадает в точку К. Расстояние АК - ВК = nλ. Почему же не всегда в точке К наблюдается интерференционный максимум?

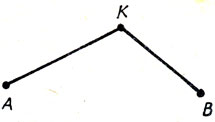
Рис. 131

 ●256. "Исчезновение" энергии при интерференции.

При определенных условиях два луча света, интерферируя, дают темноту. При этом энергия колебаний в этих точках равна нулю.

С другой стороны, каждый луч несет с собой некоторую энергию (с лучом связан поток энергии).

Не противоречит ли явление интерференции закону сохранения энергии: два потока энергии, складываясь, дают нуль?