21. Геометрическая оптика

 ○257. Когда светлое пятно на экране подобно форме отверстия?

Если через малое отверстие любой формы (квадратное, треугольное) в листе картона пропустить в комнату пучок солнечных лучей и принять его на экран, поставленный перпендикулярно к лучам, то получается круглое изображение солнца. Если же отверстие достаточно велико, то изображение на экране представляет фигуру, подобную фигуре отверстия. Объясните парадокс.

 ○258. Одинаковы ли размеры предмета и его изображения в плоском зеркале?

Наблюдатель К видит предмет АВ и его изображение в плоском зеркале CD (рис. 132). Размеры предмета и изображения представляются ему различными. Но ведь известно, что плоское зеркало не изменяет размеров светящегося предмета. Как разрешить это противоречие?

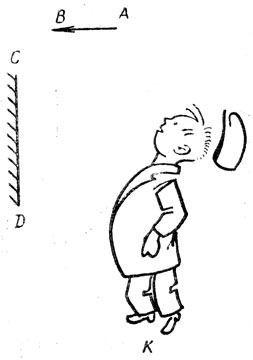
Рис. 132

 ○259. Можно ли осветить изображение?

В плоском зеркале АВ получено мнимое изображение предмета C₁D₁ (рис. 133). Если из Н направить параллельный пучок лучей в направлении на изображение C₁D₁, то можно заметить, что оно становится светлее. Но ведь за зеркалом изображение Мнимое! А кроме того, лучи за зеркало проникнуть не могут. Как же объяснить парадокс?

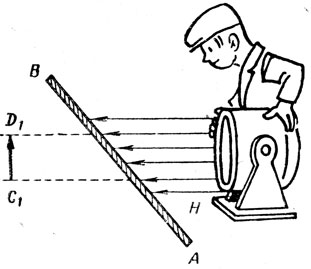
Рис. 133

 ●260. почему плоское зеркало не дает обратного изображения?

При отражении в плоском зеркале наша правая и левая стороны меняются своими местами. А верх и низ остаются неизменными. Нет ли здесь противоречия?

 ○261. Плоское зеркало дает перевернутое изображение.

Плоское зеркало дает прямое, мнимое и симметричное изображение.

Система двух плоских зеркал, следует ожидать, должна также дать прямое и мнимое изображение. Однако, если рассматривать в двух плоских зеркалах, расположенных под прямым углом КОМ (рис. 134), предмет АВ, наблюдается его мнимое и перевернутое изображение. Объясните парадокс.

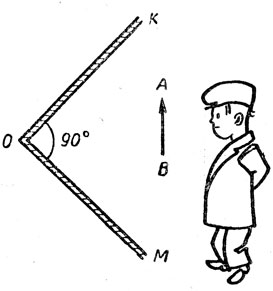
Рис. 134

 ○262. Всегда ли изображение в зеркале мнимое?

Всякую вогнутую сферическую зеркальную поверхность можно рассматривать как совокупность бесконечно малых плоских зеркал. Изображение в плоском зепкале всегда

мнимо. Следовательно, во всяком вогнутом зеркале общее изображение тоже должно быть всегда мнимым. Но это заключение, вообще говоря, не совпадает с опытом - вогнутое зеркало в ряде случаев дает действительное изображение. Как разрешить этот парадокс?

 ●263. Действительное изображение или мнимое?

Светящаяся точка А находится в фокальной плоскости зеркала. Общепринятое построение изображения (рис. 135) дает действительное А₂ и мнимое А₁ изображения. Почему получилось противоречие?

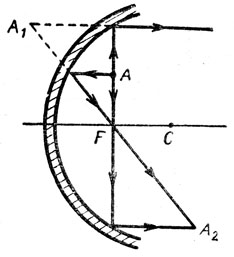
Рис. 135

 ○264. Как и куда смотреть?

Вогнутое сферическое зеркало, радиус отверстия которого - величина того же порядка, что и радиус сферы, дает на экране размытое действительное изображение. Однако при рассматривании этого изображения в зеркале оно видно четким (хотя и искаженным). Нет ли здесь противоречия?

 ●265. Задача-шутка.

Учитель: "Недалеко то время, когда Луна будет заселена людьми".

Ученик: "Люди не смогут поселиться на Луне, так как им надо будет покидать ее, когда она будет принимать форму узкого серпа". Имеет ли физический смысл подобное утверждение?

 ●266. Возможно ли это?

Инженеры-конструкторы давно ищут способ концентрации большой лучистой энергии в малом объеме. Хорошо известен фантастический "гиперболоид инженера Гарина". Широкое применение в наше время получают лазеры и мазеры.

Один изобретатель предложил устройство для концентрации лучистой энергии, основной частью которого является коническая зеркальная труба, от внутренней поверхности которой отражаются лучи, посылаемые источником С (рис. 136). Совершив ряд отражений, эти лучи выйдут через отверстие О, которое можно сделать сколь угодно малым и, следовательно, достичь сколь угодно большой мощности светового потока. В чем ошибка проекта?

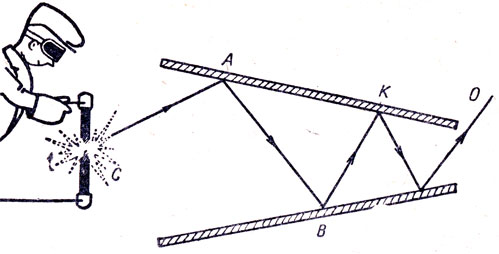
Рис. 136

 ○267. Почему пена непрозрачна?

Воздух прозрачен для света, вода также. А пена - пузыри воды, наполненные воздухом,- непрозрачна.

Аналогично одеколон и вода дают непрозрачную смесь молочного цвета, туман или облако непрозрачны, хотя состоят из прозрачных капелек воды. Объясните парадокс.

 ○268^*. Почему дно водоема видно четким?

Лучи, исходящие из какой-либо точки предмета С (рис. 137), находящегося в воде, проходят сквозь плоскую границу между водой и воздухом. Где находится изображение точки С?

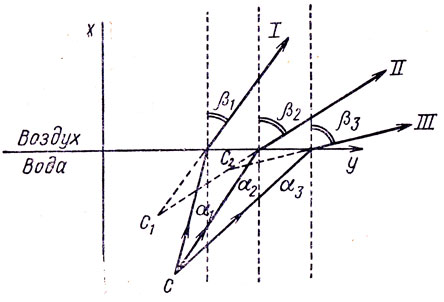
Рис. 137

Решение. Возьмем три луча, лежащие в вертикальной плоскости XOY, причем ось У направлена вдоль поверхности воды. Уравнения лучей внутри воды имеют вид:

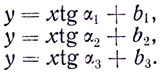
Так как они исходят из одной точки С, то имеет место соотношение:

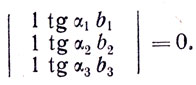
Уравнения преломленных лучей имеют вид:

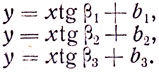
Так как tgα₁:tgα₂: tgα₃ ≠ tgβ₁:tgβ₂:tgβ₃, то

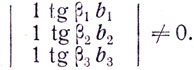
Это означает, что преломленные лучи не имеют общей точки, т. е. продолжения направлений преломленных лучей в сторону воды не пересекаются в одной точке. Значит, нет изображения точки С. И все же, глядя на дно водоема, мы видим его четко. Как разрешить этот парадокс?

 ○269. Где самое глубокое место водоема?

Если стоять по пояс в воде водоема, дно которого горизонтально, то профиль дна представляется таким, как на рисунке 138, причем самым глубоким местом будет то, в котором находится наблюдатель А. Как объяснить этот парадокс?

Рис. 138

 ○270. Нет ли здесь волшебства?

Мимо большого стеклянного аквариума в форме параллелепипеда (рис. 139) на близком расстоянии (примерно полметра) проходит наблюдатель параллельно одной из его граней. При этом происходит следующее явление: когда наблюдатель подходит к аквариуму, все находящиеся в воде предметы (камни, растения, неподвижные рыбы) как бы удаляются от стекла, на которое он смотрит, а при удалении наблюдателя от аквариума эти предметы снова как бы приближаются к стеклу. Объясните этот парадокс зрения.

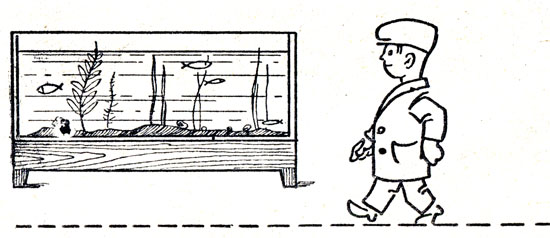
Рис. 139

 ○271. Оконное стекло не дает смещения предметов.

Плоскопараллельная пластинка смещает проходящий через нее луч параллельно самому себе.

Оконное стекло - плоскопараллельная пластинка. Однако (вопреки логике) при рассматривании -предметов через оконное стекло они не кажутся смещенными? Как разрешить парадокс?

 ○272. Равен ли день ночи во время равноденствия?

Астрономические вычисления указывают, что во время равноденствия продолжительность дня и ночи одинакова.

Однако истинная продолжительность дня всегда больше той, которую дают астрономические вычисления. Например, 23 сентября 1968 г. продолжительность дня (по календарю) составляла 12 ч 11 мин. Нет ли здесь противоречия?

 ○273. Парадокс лунного затмения.

Лунное затмение происходит лишь в том случае, когда Луна попадает в тень, отбрасываемую Землей.

Иногда лунное затмение происходит в то время, когда Солнце и Луна находятся у диаметрально противоположных точек горизонта, но непосредственно над горизонтом, когда Луна никак не может находиться внутри конуса тени, отбрасываемой Землей. Как объяснить этот парадокс?

 ○274. Когда бумага становится прозрачной?

Бумага - тело, почти непрозрачное для света. Стеарин также непрозрачен. Но стеариновое пятно на бумаге прозрачно. Как объяснить этот парадокс?

 ○275. О параллельных пучках света.

В учебниках физики указывается, что параллельный пучок лучей не может быть реализован на опыте. Однако основным свойством линзы считается, получение с ее помощью параллельного пучка, если источник расположен в фокусе линзы. Нет ли здесь противоречия?

 ○276. Видит ли глаз предметы прямыми?

Двояковыпуклая линза дает на экране перевернутое изображение предмета. Хрусталик глаза - двояковыпуклая линза. Значит, в глазу на сетчатке получается перевернутое изображение. Однако мы не видим окружающие нас предметы перевернутыми. Объясните парадокс.

 ○277. Где источник света?

Легонько нажмите пальцем на левое глазное яблоко со стороны переносицы (в правой части глаза). Тогда видны светлые круги в левой части глаза. Их происхождение - механическое раздражение сетчатки. Но ведь это раздражение было в правой, а не в левой части глаза. Как объяснить это несоответствие?

 ○278. И глаз может ошибаться.

Проколите маленькое отверстие в куске бумаги и держите его очень близко от глаза, смотря против света. Между отверстием и глазом поместите булавку головкой вверх. Изображение булавки получается головкой вниз. Объясните парадокс.

 ○279. Почему видит глаз?

Если предмет находится в фокальной плоскости собирающей линзы (или зеркала), изображение предмета на экране/как видно из геометрического построения (рис. 135), не получается. Почему же мы все-таки "видим" изображение, если смотрим через линзу на предмет, находящийся в фокальной плоскости? Как разрешить это противоречие?

 ○280. Что такое струи дождя?

Дождь - это движущиеся капли воды. Мы видим не капли, а струи. Как объяснить этот парадокс?

 ○281. Куда вертятся колеса?

На экране кино колеса экипажа нередко вертятся в направлении, не соответствующем направлению движения экипажа. Как объяснить этот парадокс?

 ○282. Как образовалось в кисти руки "отверстие"?

Сверните трубку из листа бумаги. Возьмите ее в левую руку. Расположите трубку перед левым глазом. Держите ладонь правой руки так, чтобы край ладони касался стенки трубки. Смотрите левым глазом в трубку, а правым на ладонь, повернутую к глазу.

В кисти руки видно круглое отверстие (рис. 140), через которое правый глаз видит то же, что и левый через трубку. Но ведь в ладони никакого отверстия нет! Как объяснить парадокс?

Рис. 140

 ○283. Почему очки не дают перевернутого изображения?

Пользуясь очками с двояковыпуклыми линзами, видят предметы прямыми, хотя они и находятся от стекол очков на расстояниях, больших двойного фокусного.

С другой стороны, известно, что изображение предмета, находящегося от выпуклой линзы на расстоянии, большем фокусного, на экране является перевернутым. Как разрешить это кажущееся противоречие?

 ●284. Почему звезды - точки, а не бесконечные плоскости?

Представим себе на очень большом расстоянии от нас какой-либо светящийся предмет (например, звезду) и неограниченных размеров светящуюся плоскость. От светящегося предмета до нас дойдет волна, которую можно принять за сферическую с бесконечно большим радиусом. От светящейся же плоскости получится волна плоская.

Вследствие незначительных размеров зрачка глаз может получить впечатление только от бесконечно малой части поверхностей, дошедших до него волн. Понятно, что очень малые части сферы с бесконечно большим радиусом и плоскости, в сущности, одно и то же. Следовательно, и зрительные ощущения в обоих случаях должны быть одинаковыми.

Таким образом, звезды должны бы казаться нам светящимися плоскостями неограниченных размеров, а не точками, как это наблюдается в действительности¹.

¹ (Нельзя думать, что в данном случае глаз улавливает незначительное отклонение лучей от параллельности, так как можно привести примеры, где и более грубые отклонения оказываются для глаза незаметными. Так, напри* мер, для установки зрительной трубы "на бесконечность" практически достаточно установить ее по удаленному на несколько километров предмету.)

 ○285. Параллельны ли лучи Солнца?

Солнечные лучи, пробивающиеся сквозь тучи, представляются радиально расходящимися во все стороны, подобно сиянию (рис. 141). Между тем солнечные лучи, падающие на Землю, параллельны. Как объяснить получившееся противоречие?

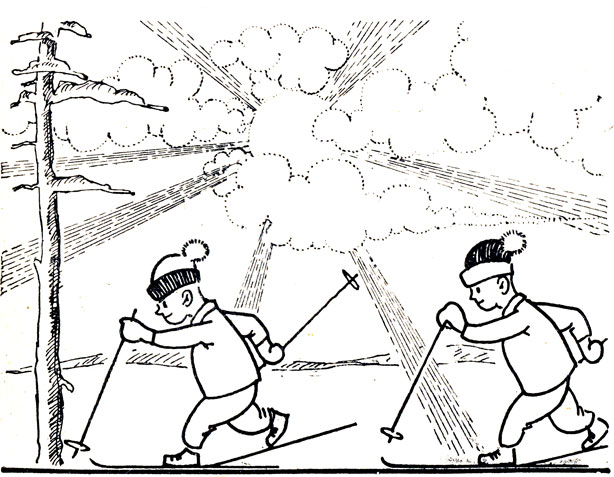
Рис. 141

 ○286. Одинаков ли угловой диаметр Луны?

Восходящая Луна нам представляется большего диаметра, чем когда она находится на большой высоте над горизонтом. Но ведь не удаляется же Луна при этом. Как объяснить парадокс?

 ○287. Какова толщина нити?

Раскаленная нить в электрической лампе кажется значительно толще той же нити в холодном состоянии. Объясните парадокс.

 ○288. Черная молния.

А. М. Горький сравнивает буревестника с черной молнией. . У А. И. Куприна есть рассказ "Черная молния", в котором читаем: "Все небо обложили громоздкие лиловые и фиолетовые тучи с разорванными серыми краями... Была одна мокрая густая тьма. Сверкнула первая молния... за ней другая, третья. Потом пошло и пошло без перерыва. ...Небо не вспыхивало от молний, а точно все сияло их трепетным голубым, синим и ярко-белым блеском... И вот я увидел черную молнию. Я видел, как от молнии полыхало на востоке небо, не потухая, а все время то развертываясь, то сжимаясь, и вдруг на этом колеблющемся огнями голубом небе я с необычайной ясностью увидел мгновенную и ослепительную черную молнию. И тотчас же вместе с ней страшный удар грома точно разорвал пополам небо и землю и бросил меня вниз, на кочки... О, что это была за ужасная ночь. Эти черные молнии наводили на меня необъяснимый животный страх". Как объяснить парадоксальное явление, называемое - "черной молнией"?