
3) Работы Галилея в области механики
Нетрудно определить, что сделано Галилеем по основным вопросам. Для этого достаточно прочитать его "Беседы", в которых он за несколько лет до своей смерти систематизировал всё, что им было сделано в этой области.
В ряде случаев разбор этих вопросов облегчается тем, что сам Галилей в этой работе указывает, что он наследовал от своих предшественников и что разработал или открыл заново.
Галилей занимался следующими основными вопросами механики:
1) равномерным движением тел;
2) законом свободного падения тел;
3) движением тел по наклонной плоскости;
4) теорией маятника;
5) законом сложения сил;
6) движением тела, брошенного под углом к горизонту;
7) разработкой понятия относительного движения.
Прежде чем перейти к рассмотрению того, что сделал Галилей в каждом из этих разделов механики, следует остановиться на некоторых общих положениях.
Галилей оставил после себя не отдельные работы или даже отрывочные записи о них, как это, например, имело место с научным наследством Леонардо да Винчи, а им самим написанное, систематизированное изложение всего того, к чему он пришёл в области механики.
Изложены эти вопросы прекрасным литературным языком, в стиле лучших традиций древних геометров. В трудах видно стремление к чёткости и глубине формулировок. Для времени Галилея это является исключительным явлением, которое может быть оценено должным образом, если мы учтём, что ни о какой установившейся терминологии в то время ещё не могло быть речи. Галилей стремился каждое из своих утверждений сопровождать основными следствиями, которые из этих утверждений вытекали.
Второе, о чём следует сказать, - это о применяемых Галилеем математических методах.
Выше говорилось, что любимым его учителем был Архимед. Галилей развил метод геометрических построений Архимеда. Для анализа законов неравномерного движения выгодней было пользоваться аналитическими методами, опирающимися на дифференциальное исчисление, но последнее было открыто много позже.
Далее будут приведены примеры того, как геометрические приёмы, которые применял Галилей, позволяли ему в отдельных случаях решать задачи значительно проще и нагляднее, чем решение их современными приёмами.
Изложение своих работ по механике Галилей* начинает с рассмотрения равномерного движения. Здесь Галилей внёс, на первый взгляд, не много нового по сравнению с тем, что по этому вопросу было известно до него. Он дал определение понятию "равномерное движение", уточнил его, исключив возможность ошибки из-за скрытой неточности предыдущих формулировок, и целым рядом задач проиллюстрировал свойства такого движения. Если внимательно прочесть это место "Бесед", то станет ясным, что Галилей ставил своей целью уточнение терминов и формулировок и иллюстрацию применяемого им математического метода.
* (См. "День третий" "Бесед".)
Иначе обстоит дело с вопросом о законах свободного падения тел. До Галилея физика располагала лишь ложным утверждением Аристотеля о том, что тело падает потому, что его толкает воздух, врывающийся в разреженную область позади тела, образующуюся при его падении.
Очевидно, Галилей не знал трудов Леонардо да Винчи по этому вопросу, но если бы и знал их, он смог бы воспользоваться лишь открытием Леонардо да Винчи по первой части вопроса. Оно состояло в том, что причиной падения тела является сила тяжести и что движение тела при этом имеет равноускоренный характер. Развивая это утверждение, Леонардо да Винчи пытался совместить несовместимое. Он указывал, что при таком равноускоренном движении не только скорость, но и пройденный путь нарастает на постоянную величину в единицу времени. Галилей начал с доказательства того, почему движение свободно падающего тела должно быть равноускоренным. В современной механике для нахождения законов свободного падения обычно пользуются вторым законом Ньютона, гласящим, что изменение количества движения тела в единицу времени равно действующей силе и направлено по этой последней. Его можно написать в виде:
(1)
| dp | = F. | |
| dt |
или, учтя, что количество движения р равно произведению массы на скорость
(2)
p = m · υ,
мы можем также написать (при условии, что изменением массы со скоростью можно пренебречь):
(3)
| m | dv | = F. |
| dt |
Отсюда, если сила равна нулю, изменение скорости тоже равно нулю. Движение тела в этом случае будет равномерным, или в частном случае тело будет в покое (скорость постоянна или равна нулю).
Если же сила равна постоянной величине, то изменение скорости будет тоже постоянной величиной, т. е. движение будет равноускоренным.
Законы Ньютона были сформулированы почти через 50 лет после смерти Галилея и ему, следовательно, приходилось начинать с обоснования, почему при постоянной величине действующей силы движение будет равноускоренным.
Доводы, которые использует для этого Галилей, многообразны. Он утверждает, что "Умом своим мы можем признать такое движение единообразным и неизменно равномерно ускоряющимся, так как в любые равные промежутки времени происходят и равные приращения скорости", и в другом месте говорит: "Поэтому, когда я замечаю, что камень, выведенный из состояния покоя и падающий со значительной высоты, приобретает всё новое и новое приращение скорости, не должен ли я думать, что подобное приращение происходит в самой простой и ясной для всякого форме?"
Но во всех этих умозаключениях больше уверенности в том, что это именно так и должно происходить, чем. убедительности, а убеждать перипатетиков-мастеров словесных узоров их же оружием вряд ли эффективно.
Как бы чувствуя это, Галилей основной упор делает на результаты опытных данных. Он говорит, например: "Мы тем не менее решили рассматривать только те явления, которые действительно имеют место в природе при свободном падении тел", и далее: "Наконец, к исследованию естественно ускоренного движения нас непосредственно привело внимательное наблюдение того, что обычно имеет место и совершается в природе".
Утверждение, что движение свободно падающего тела происходит равноускоренно, является само по себе большим открытием, но не решает полностью задачи.
В современной механике исходное выражение для равноускоренного движения пишется в виде:
| m | dv | = F |
| dt |
или, чго то же:
(4)
| dv = F | = g; | |
| dt = m |
отсюда легко можно вывести остальные выражения, которые нужно знать, чтобы судить о законах равноускоренного движения.
Выражение для изменения скорости со временем может быть написано в вида:
(5)
υ = gt,
учтя, что
| v = | ds | , |
| dt |
мы можем написать выражение для пройденного пути:
(6)
| S = | gt2 | ; |
| 2 |
отсюда для величины времени, необходимого для того чтобы пройти путь S, можно написать следующее выражение:
(7)
| t = √ | 2s | |
| g |
и для скорости, которую будет иметь тело в конце заданного пути:
(8)
υ = √2gS
Методы математического анализа для таких вычислений были разработаны Лейбницем значительно позже, а пока Галилею приходилось искать другие пути. Он находил их при помощи излюбленной им геометрии, причем наглядным путём устанавливал все те соотношения, имеющие место при равноускоренном движении, которые были приведены выше. Во второй, третьей и четвёртой темах VII главы применение этих методов будет разобрано на конкретных примерах.
До последнего времени, когда хотят основы механики изложить возможно нагляднее, без применения высшей математики или даже минимального использования алгебры, прибегают в ряде случаев к геометрическим построениям Галилея*.
* (См., например, Н. Фадеев, Экспериментальная механика, изд 13, ГОНТИ. 1931.)
Леонардо да Винчи положил начало современному представлению о законах свободного падения тела и заложил основы этой области механики.
Полное открытие законов движения свободно падающих тел безусловно принадлежит Галилею.
Совершенно естественно, что следующим шагом в деле изучения движения тел под действием силы тяжести было изучение движения по наклонной плоскости. Если Леонардо да Винчи, который в этой области является первым, интересовался наклонной плоскостью главным образом как простейшей машиной, где можно за счёт скорости получить выигрыш в силе, то Галилей интересовался законами движения тел по наклонной плоскости под действием силы тяжести как средством повышения точности экспериментального изучения законов свободного падения.
Можно предполагать, что вопросами движения маятника Галилей занимался раньше, чем движением тел по наклонной плоскости, но в "Беседах" рассмотрение второго вопроса, для логичности изложения, предшествует рассмотрению теории маятника.
В этом разделе Галилей подробно рассматривает вопросы о зависимости конечной скорости движения от высоты наклона, о Сохранений равноускоренности при движении тела по наклонной плоскости под действием силы тяжести, о времени движения в зависимости от наклона и ряд других вопросов, связанных с движением по наклонной плоскости.
Для характеристики того, какое место в механике Галилея занимали вопросы движения тел по наклонной плоскости, достаточно сказать, что из двадцати двух теорем, приведённых в "Дне третьем" "Бесед", двадцать посвящены этому вопросу и только две - вопросам свободного падения.
Сам Галилей говорил, что вопросом движения по наклонной плоскости он заинтересовался потому, что видел в нём возможность получения равноускоренного движения, значительно замедленного по сравнению со свободным падением. Тем самым он надеялся повысить точность экспериментальной проверки утверждения Аристотеля, что скорость падения тела зависит от его тяжести.
Он говорил: "Чтобы иметь дело с движением по возможности медленным, при котором уменьшается сопротивление среды, изменяющее явление, обусловливаемое простой силой тяжести, я придумал заставлять тело двигаться по наклонной плоскости, поставленной под небольшим углом к горизонту; при таком движении совершенно так же, как при свободном отвесном движении, должна обнаружиться разница, происходящая от веса".
Если следовать за биографами Галилея, то поиски путей повышения точности измерения скорости падения тел разной тяжести Галилей начал путём изучения движения маятника ещё сравнительно в раннем возрасте.
В самом деле, если рассматривать движение маятника как последовательный ряд падений и подъёмов тела по дуге окружности, то при независимости характера изменения скорости движения тела от его тяжести, маятники одинаковой длины должны качаться одинаково, вне зависимости от величины подвешенных грузов. Таким образом, имелась возможность очень наглядно проверить справедливость утверждений Аристотеля о влиянии веса тел на скорость их падения. Галилей провёл подобные опыты. Результаты своих исследований он описывал следующим образом: "Для этого я взял, в конце концов, два шара-один из свинца, другой - из пробки, причём первый был в сто раз тяжелее второго, и прикрепил и подвесил их на двух одинаковых тонких нитях длиной в четыре или пять локтей; когда, затем, я выводил тот и другой шарик из отвесного положения и отпускал их одновременно, то они начинали двигаться по дуге круга одного и того же радиуса ... после того как шарики производили сто качаний туда и обратно, становилось ясным, что тяжёлый движется столь согласованно с лёгким, что не только после ста, но после тысячи качаний не образуется ни малейшей разницы во времени".
Может быть, потому, что маятник служил Галилею лишь для экспериментальных целей, он не развил до конца его теорию*.
* (Об этом подробнее рассказано в пятой теме VII главы.)
Так же, как в вопросах исследования свободного падения тел и в вопросах сложения и разложения сил, Галилей повторно открыл то, что уже сделал до него Леонардо да Винчи, а затем существенно развил этот вопрос. Леонардо показал, что силу в ряде случаев удобно представлять в виде двух составляющих. Это он продемонстрировал при анализе движения тел по наклонной плоскости, где силу тяжести он разложил на силу, направленную по движению тела, и на силу, придавливающую тело к наклонной плоскости.
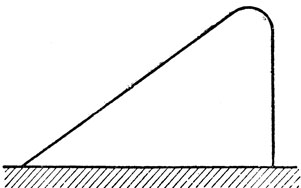
Рис. 1
Леонардо правильно выбрал направление этих сил, но не указал, как количественно определить их величину. Галилей в своих рассуждениях о параболическом движении брошенного тела показал, что он имеет представление о сложении сил хотя бы для случая, когда они перпендикулярны друг к другу. Трудно установить., в какой степени были известны ему при этом труды его современника Стевина, который много работал над вопросами сложения сил. Стевин занимался этим вопросом как чисто геометрической задачей, а Галилей развил его применительно к параболическому движению тела, брошенного под углом к горизонту.
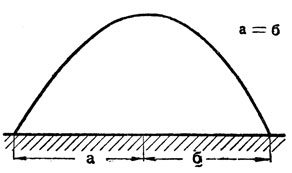
Рис. 2
Вопрос о том, как движется тело, брошенное под углом к горизонту, занимал ещё учёных древности. На основе учения Аристотеля считалось, что тело, брошенное под углом к горизонту, сначала летит прямолинейно, потом описывает дугу круга и далее падает вертикально вниз (см. рис. 1). Подобная кривая считалась правильной, пока Леонардо да Винчи не ввёл в рассуждения понятия, являющиеся прообразом современных представлений об инерции. Правда, сначала он считал, что обе ветви кривой должны быть симметричны (см. рис. 2), но в последующем понял, какова должна быть в действительности траектория тела, брошенного под углом к горизонту, и изображал её так, как это показано на рисунке 3.
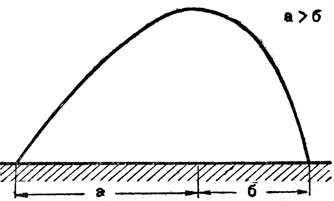
Рис. 3
Итальянский учёный Тарталья, которого некоторые историки называют основоположником баллистики, в своём труде, опубликованном в середине XVI в., углубил представления о характере движения брошенного тела. Он утверждал, что тело летит в этом случае по кривой, кривизна которой непрерывно меняется,
Но в действительности первым, достаточно полно для своего времени, исследовал этот вопрос лишь Галилей. Он доказал, что кривая, по которой летит тело, брошенное под углом к горизонту, является параболой.
Галилей показал также приёмы вычисления этой параболы, исходя из того, что в любой точке на тело действует сумма двух сил*. Он понимал, что полученные им параболические кривые движения в действительности несколько отличны от истинных за счёт трения летящего тела о воздух.
* (Подробнее этот вопрос будет разобран в пятой теме VII главы.)
Во всяком случае, Галилей не только опроверг выводы механики Аристотеля, как это сделал в своё время Леонардо да Винчи, но показал также, к какому виду движения приводят новые исходные положения.
Обратимся теперь к одному из важнейших открытий в области механики-открытию так называемого принципа относительности Галилея. Наблюдая механические процессы в движущихся системах (например, на корабле), Галилей установил, что эти процессы протекают совершенно одинаково, покоится ли система или движется равномерно и прямолинейно.
На современном языке этот принцип можно сформулировать так: в системах, движущихся друг относительно друга равномерно и прямолинейно, любые одни и те же механические опыты дают одинаковые результаты.
Принцип относительности Галилея. Галилей, например, утверждал, что при равномерном и прямолинейном движении корабля при помощи механических опытов нельзя обнаружить, движется корабль или нет. Если подбросить вверх какой-нибудь предмет или следить за каплей воды, падающей с верхнего сосуда в нижний, то для наблюдателя на корабле все эти процессы будут казаться одинаковыми, вне зависимости от того, имеет ли место прямолинейное и равномерное движение корабля или он находится в покое.
Этот принцип справедлив лишь при малых, относительно скорости света, скоростях движения. Для скоростей, близких к скорости света, и для сложных электромагнитных процессов он неприменим.
В настоящее время создана теория относительности, покоящаяся на более общих принципах. Однако принцип относительности Галилея для развития механики был очень плодотворным.
|
ПОИСК:
|