
Разбор основных тем по физике Галилея

Тема первая: Равномерное движение
Утверждения Галилея
("Беседы": а) стр. 323; б) стр. 329; в) стр 306; г) стр. 331; Д) стр. 335; е) стр. 336; ж) стр. 344; з) стр. 349.)
а) Движением равномерным, или единообразным, я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собой.
б) Если равномерно движущееся тело проходит с постоянной скоростью два расстояния, то промежутки времени прохождения последних относятся между собой, как пройденные расстояния.
в) При неравных скоростях, на равных пройденных расстояниях, отношение скоростей равно обратному отношению промежутков времени.
г) Если два тела движутся равномерно, то отношение скоростей их равняется отношению пройденных расстояний, умноженному на обратное отношение времён движения.
Разбор утверждений
В вопросах равномерного движения Галилей, на первый взгляд, не открыл ничего нового. Все эти утверждения могут быть найдены в той или иной форме у ряда Других учёных, начиная от древних.
Линейные пропорции, в которых выражались величины, характеризующие равномерное движение, до того, как в механику вошла алгебра и высшая математика, позволяют в этом случае доказывать большое число теорем, пересказывая в разных комбинациях соотношения между скоростью, временем и величиной пройденного пути.
Если всё же в этой книге проводится разбор утверждений Галилея и по вопросам равномерного движения, то это диктуется двумя соображениями.
Первое из них состоит в том, что, разбирая эти утверждения, мы убеждаемся, насколько уже чётка терминология и формулировки в механике Галилея и насколько они приближаются к современным. Недаром в течение нескольких веков во многих учебниках физики и механики дословно переписывались эти теоремы
В книге Галилея "Беседы", которой он завершил свою творческую жизнь и в которой он обобщил все свои работы по механике, раздел, посвященный равномерному и равноускоренному движению ("День третий"), начинается с утверждений, приведённых выше. Он нужен Галилею для установления терминологии и для иллюстрации методики. Это удобнее сделать на простейших вопросах равномерного движения.
Галилей нигде не пользуется алгеброй ни для доказательств, ни для записей формулировок теорем. Если бы он это сделал, то утверждения "б", "в", "г" можно было бы записать в виде:
(б)
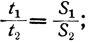
(в)
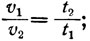
(г)
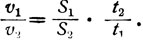
Причём все эти выражения можно было бы вывести как следствие из исходного выражения для равномерного движения:
S = υ · t
Галилей пользуется геометрическими методами доказательств и, следуя традициям древних геометров, для убедительности этих доказательств чётко идёт от более простого к более сложному. Этим и объясняется, почему при разборе принципиально нового для того времени вопроса о равноускоренном движении Галилей начинает с привычных, уже установившихся взглядов и на них приучает к чётким строгим формулировкам.
Вторая, весьма характерная особенность утверждений Галилея состоит в стремлении к полноте формулировок. В этом отношении характерно утверждение, приведённое в пункте "а". Здесь прибавление слова "любые" делает старое утверждение, известное по своей идее ещё до Галилея, более полным и строгим.
Сам Галилей придавал этому большое значение. Так, он говорил: "К существовавшему до сего времени определению (которое называло движение равномерным, просто, при равных расстояниях, проходимых в равные промежутки времени) мы прибавили слово "любые", обозначая тем какие угодно равные промежутки времени, так как возможно, что в некоторые определённые промежутки времени будут пройдены равные расстояния, в то время как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны".
Доказательства утверждениям, приведённым выше, Галилей строит в виде геометрических теорем в их классической форме. Здесь и доказательства от обратного, и сравнение отрезков масштабных линий, и допущения.
Заключение
В своих утверждениях по вопросам равномерного движения Галилей не внёс ничего принципиально нового, сущность вопроса толковалась правильно и до него. Он только чётко сформулировал основные положения, применив терминологию, схожую с принятой в наше время.
Он также указал на необходимость чёткости и полноты формулировок. Он показал, например, в утверждении, приведённом в пункте "а", что введение одного только слова исключает возможность ошибки, которая таилась в формулировках предшественников.
Тема вторая: Законы свободного падения тел
Утверждения Галилея
(Как уже указывалось выше, основные труды Галилея-"Беседы" и "Диалог" написаны в виде обмена мнениями между рядом лиц Когда берутся утверждения из этих книг они основываются на высказывании того собеседника который, бесспорно, госорит от имени Галилея. Утверждения взяты из "Бесед": а) стр. 144; б) стр. 306; в) стр. 311; г) стр. 313; д) стр 315. )
а) Я не сомневаюсь в том, что одно и то же тело в одной и той же среде имеет постоянную скорость, определенную природой, которая не может увеличиться иначе, как от приложения новой силы, или уменьшится иначе, как от препятствия, замедляющего движение.
б) Равномерно, или единообразно, ускоренное движение есть такое, при котором в равные промежутки времени прибавляются и равные моменты скорости.
в) Время, в течение которого тело, вышедшее из состояния покоя и движущееся равномерно ускоренно, проходит некоторое расстояние, равно времени, в течение которого это же расстояние было бы пройдено тем же телом при равномерном, движении, скорость которого равняется половине величины наибольшей конечной скорости, достигаемой при первом равномерно ускоренном движении.
г) Если тело, выйдя из состояния покоя, падает равномерно ускоренно, то расстояния, проходимые им за определённые промежутки времени, относятся между собой, как квадраты времени.
д) Таким образом, в то время как скорость возрастает в равные промежутки времени как простой ряд последовательных чисел, расстояния, пройденные за те же промежутки времени, относятся между собой, как последовательные нечётные числа.
Разбор утверждений
Как уже говорилось в IV главе, для исследования за-в свободного падения в том виде, как это принято в наше время, у Галилея не было математического аппарата, который был разработан в последующие века. Он использовал столь излюбленные им геометрические методы Архимеда, и это наложило известный отпечаток не только на терминологию, но и на всю методику разработки этого вопроса.
С точки зрения формы - это изложение вопроса в виде теорем, лемм и следствий из них, С точки зрения содержания - это стремление изобразить зависимости в виде пропорций. Это часто мешает выразить закон достаточно полно. Например, при рассмотрении свободного падения, это приводит к тому, что уделяется много внимания вопросам сравнения скоростей, сопоставлению величин пройденного пути, но почти совершенно не указываются методы абсолютного определения этих величин.
Перейдём теперь к разбору отдельных утверждений.
В утверждении "а" Галилеем изложены положения, которые легли в основу того, что мы называем первым законом Ньютона. В нём выражено стремление тела сохранить движение и возможность изменения характера этого движения лишь за счёт внешней силы. Недаром первый закон Ньютона во многих учебниках в подзаголовках называют "законом Галилея".
Предположение Галилея о стремлении всякого тела сохранять своё движение (закон инерции)* находилось в коренном противоречии с господствовавшими до этого взглядами, что тело движется только тогда, когда к нему приложена внешняя сила.
* (Ведь то, что сделал в этой области Леонардо да Винчи, лежало под спудом.)
Эта тема начата с утверждения Галилея о равномерном движении потому, что без него трудно понять ход мышления Галилея. В самом деле, если равномерное движение имеет место всегда, когда тело находится лишь под действием инерции, то любое приложение внешней силы Должно нарушить характер этого движения. Возникает вопрос: каков же должен быть характер движения при наличии внешней силы?
Мы уже приводили выше высказывания самого Галилея, что в вопросах изучения законов свободного падения он видит свои заслуги не в том, что он указывал на ускоренный характер этого падения*. Основной своей заслугой Галилей считал утверждение о равноускоренном характере этого движения.
* (Он сам говорил в предисловии к "Третьему дню" "Бесед", что это знали задолго до него.)
Галилей много внимания уделил тому, чтобы доказать, почему движение свободно падающего тела обязательно должно быть равноускоренным, Начинает он с доводов умозрительного характера, Он, например, говорит:
"Когда я замечаю, что камень, выведенный из состояния покоя и падающий со значительной высоты, приобретает всё новое и новое приращение скорости, не должен ли я думать, что подобное приращение происходит в самой простой и ясной для всякого форме? Если мы внимательно всмотримся в дело, то найдём, что нет приращения более простого, чем происходящее всегда равномерно".
И заключает он словами: "Наконец, к исследованию естественно ускоренного движения нас непосредственно привело внимательное наблюдение того, что обычно имеет место и совершается в природе".
На основании всех своих рассуждений он приходит к выводу, что единственно возможным движением свободно падающего тела является равноускоренное движение.
В трудах Галилея мы можем найти страницы, посвящённые доказательству того, что тело набирает скорость равномерно, без скачков, что падающее тело начинает своё движение с ничтожно малых скоростей, а не сразу скачком набирает скорость, как это казалось многим его современникам и как это часто кажется наблюдателю.
Галилей даёт определение равноускоренного движения в том виде, как оно изложено в пункте "б". Это определение современными средствами математики может быть записано в форме:
υ = gt,
где υ - скорость в данный момент,
g - ускорение силы тяжести,
t - время.
Сделав это исходное утверждение, мы можем, как это показано было в выражениях 5 - 8 главы IV, средствами дифференциального исчисления найти ответ на все интересующие нас вопросы о характере движе-ния равноускоренно падаю-щего тела, Однако в распоряжении Галилея этих средств ещё не было, и он должен был ещё искать пути решения задач механики.
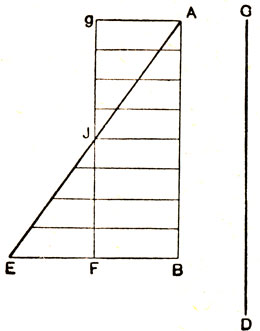
Рис. 6
Как мы уже говорили, Галилей, следуя Архимеду, широко использовал геомет-рию для решения механических задач.
Для характеристики геометрических методов, применяемых Галилеем, ниже будет приведён дословный текст доказательства теоремы, приведённой в утверждении "в".
"Пусть линия АВ (см. рис. 6) представляет время*, в течение которого тело, выйдя из состояния покоя в точке С, проходит при равномерно ускоренном движении расстояние CD, Отметим, далее, степени скорости, приобретаемые телом в конце каждой отдельной частицы времени АВ; степени эти, постепенно увеличиваясь, возрастают в конце до величины ЕВ, которую и отложим на линии, перпендикулярной к АВ; соединив точки А и Е и проведя линии, параллельные ЕВ, на равных друг от друга расстояниях, отложенных на АВ, мы представим таким способом возрастающие степени скорости, начиная от А.
* (Построение, в котором время выражается линией геометрического чертежа, было смелым приёмом Галилея.)
Разделим линию ЕВ пополам в точке F и проведём линии Fg и Ag, параллельные А В и, соответственно, BF. Параллелограм AgFB будет равен треугольнику АЕВ, так как линия gF делит АЕ пополам в точке I; если поэтому продолжить параллельные линии, заключённые в треугольнике АЕВ до линии Ig, то сумма параллельных линий, заключённых в четырёхугольнике, будет равна сумме тех же линий, заключённых в треугольнике АЕВ; в самом деле, сумма тех из них, кои заключены в треугольнике IEF, равна сумме заключённых в треугольнике gIA, остающиеся же части, заключённые в трапеции AIFB, являются общими. Так как каждой отдельной частице времени А В соответствует и отдельная точка на линии А В, а проведённые через эти точки параллели, заключённые в треугольнике АЕВ, представляют возрастающие степени скорости, в то время как такие же параллели, заключённые внутри пара плелограма, представляют равную им совокупность равномерных скоростей, то ясно, что все моменты скорости ускоренного движения представлены возрастающими параллельными линиями треугольника АЕВ, а равномерного движения - аналогичными линиями параллелограма gB. то, чего не достаёт моментам в первое время движения (т. е. моментам, представленным параллельными линиями, заключёнными в треугольнике AgJ), возмещается моментами, представленными параллельными линиями треугольника IEF. Отсюда следует, что два тела пройдут равные расстояния в одно и то же время, если одно, выйдя из состояния покоя, будет двигаться равномерно ускоренно, а другое-просто равномерно со скоростью, равной половине максимальной степени скорости, достигнутой при ускоренном движении, что и требовалось доказать".
Вели провести это же доказательство, пользуясь уравнением 1, то оно будет иметь следующий вид.
Скорость, которую приобретает падающее тело через промежуток времени t0 после начала падения, будет равна:
(2)
υ0 = gt0;
путь, пройденный в это же время, определится из выражения*
* (См уравнение 6, главы IV.)
(3)
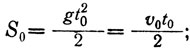
при равномерном же движении
(4)
υ = const.
(5)
S = υ · t.
Откуда следует, что для того, чтобы S = S0 и t = t0, требуется выполнение условия , что и доказывал Галилей.
В этом случае, как и в ряде других, геометрические доказательства Галилея более многословны, чем современные алгебраические, но, как будет видно далее, они в отдельных случаях значительно нагляднее и даже проще.
В утверждении пункта "г" Галилей высказывает принципиально новые положения. Даже гениальная прозорливость Леонардо да Винчи не дала ему возможности понять, что квадратичная зависимость между пройденным путём и временем, за которое этот путь пройден, является характерной особенностью равноускоренного движения.
Если записать это утверждение алгебраическим языком, то оно будет иметь вид:
(6)
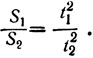
От этого утверждения до зависимости
(7)
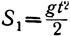
всего один шаг.
Насколько он был близок к этому, видно из утверждения "д". В самом деле, из него следует, что S=at2, и только не доказано, что коэффициент пропорциональности а равен половине ускорения.
Само же доказательство этого утверждения может быть проведено следующим образом. Приняв, что скорость в единицу времени вырастает на единицу своего измерения, мы можем скорость в конце каждой последующей единицы времени изобразить в виде простого ряда чисел:
(8)
1, 2, 3, 4, 5...n, n+1, n+2...
Поскольку пройденный путь за единицу времени ΔS в любой промежуток равен разности между путём, пройденным за п единиц времени, и путём, пройденным за n - 1 единиц времени, то мы можем написать:
а так как выражение 2n - 1 в общем виде представляет собою ряд нечётных чисел, уравнение 9 и подтверждает закономерность, приведённую в пункте "г",
Сам Галилей доказывает это последовательным сравнением площадей фигур, получаемых в треугольнике движения, аналогичного приведённому на рисунке 6.
Заключение
Разрабатывая вопросы равноускоренного движения, Галилей показал, что именно такое движение свойственно свободно падающему телу. Он дал строгое определение этому виду движения, показал, как нарастает в этом случае скорость, указал, по какому закону нарастает величина пройденного пути.
Чтобы выведенные законы движения свободно падающего тела были полными, ему надо было отойти от принятого им сравнительного метода и дать прямые зависимости между скоростью, ускорением, временем и пройденным путём.
Законы движения свободно падающего тела были выведены Галилеем для идеализированных условий, без учёта трения. Это не значит, что он не понимал влияния трения на характер происходящих при свободном падении процессов. В шестой теме этой главы будет показано, как глубоко уже были поняты Галилеем эти вопросы. Только стремление к ясности и последовательности изложения, столь свойственного трудам Галилея, заставило его разделить рассмотрение этих вопросов.
Тема третья: Движение тел по наклонной плоскости
Утверждения Галилея
а) То, что доказано в отношении падения тел в вертикальном направлении, справедливо и в отношении падения по любым наклонным плоскостям; и в этом, случае скорость увеличивается по тому же закону, т. е. в соответствии с ростом времени, иными словами, как последовательный ряд целых чисел.
б) Скорости тела, опускающегося естественным движением с одной и той же высоты по плоскостям, имеющим различный наклон, при достижении горизонта всегда равны между собой, если все препятствия к движению устранены.
в) Степени скорости, приобретаемые одним и тем же телом при движении по наклонным плоскостям, равны между собой, если высоты этих наклонных плоскостей одинаковы.
г) Если одно и то же тело, выйдя из состояния покоя, движется по наклонной плоскости и вертикали, равной высоте наклонной плоскости, то времена падения тела относятся между собой, как длина наклонной плоскости к длине вертикали.
д) Отношение времён падения по плоскостям, различающимся по наклону, длине и высоте, составляется из отношения длин и обратного отношения корней квадратных из высот наклонных плоскостей.
е) Если из высшей точки круга, построенного над горизонтом, проведены различные наклонные плоскости, доведённые до окружности, то времена падения по ним одинаковы.
ж) Если высоты двух наклонных плоскостей относятся между собой, как квадраты длин, то последние проходятся телом, вышедшим из состояния покоя, в одинаковое время.
з) Времена падения по плоскостям, имеющим различный наклон, но одинаковую высоту, относятся между собою, как длины этих плоскостей, как в том случае, когда движение начинается с выхода из состояния покоя, так и в том, когда ему предшествует падение с одинаковых высот*.
* ( "Беседы", а) стр. 282; б) стр. 282; в) стр. 286; г) стр. 290. Утверждения являются теоремами, предпосланными Галилеем и "Дне третьем" разделу "О местном движении".)
Разбор утверждений
Галилей обратился к изучению движения тела по наклонной плоскости как к. средству уменьшения ускорения тела при уменьшении наклона. Таким образом он надеялся увеличить точность экспериментальной проверки законов падения тела. Для этого ему нужно было доказать, что закон равноускоренного движения, которому подчиняется свободное падение, сохраняется и для движения тела по наклонной плоскости (этот закон изложен Галилеем в утверждении, приведенном в пункте "а").
Доказательство Галилей проводил тем же путём, как это было сделано для свободного падения. Но он, очевидно, считал, что, поскольку доказательства эти построены на умозаключениях, они недостаточно убедительны, Поэтому Галилей проделал следующий опыт для проверки своих выводов. Он брал доску, делал в ней хорошо отполированный желобок и пускал по ней шарик при разных наклонах доски, Доска была разделена на разные отрезки. Фиксируя время, которое требуется шарику, чтобы пройти сначала одну единицу длины, потом две и так далее, Галилей для каждого из наклонов находил зависимость между пройденным путём и нужным для этого временем*. Оказалось, что полученные результаты достаточно точно представляли последовательный ряд нечетных чисел**.
* (Время Галилей измерял по количеству воды, вытекавшей из калиброванного отверстия которое открывалось в начале движения и закрывалось при достижении шариком заданной отметки. При таком методе трудно говорить о "достаточной точности". )
** (Говоря языком алгебры, в этом случае имела место завиимость:
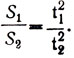
)
Для большей убедительности результатов Галилей решил исследовать, как меняется величина ускорения с изменением наклона. Для этого он вначале утверждает, что при равных высотах наклонных плоскостей, вне зависимости от угла наклона, скорости тела в конце будут одинаковы (см. пункты "б" и "в").
Доказательство этих утверждений Галилей проводит следующим образом: он берёт прямоугольный треугольник, гипотенуза которого равна длине наклонного пути, а один из катетов - высоте падения тела h. Отложив на гипотенузе, начиная с верхней её точки (см. рис. 7), отрезок, равный высоте, он последовательно приходит к выводу, что:
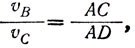
т. е. υb = υc,
где υb - скорость в точке В,
υc - скорость в точке С.
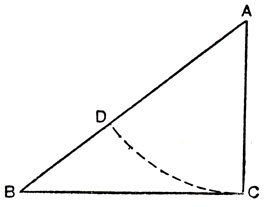
Рис. 7
Доказав это, легко показать, что величины ускорения тела при его движении по вертикали и наклонному пути, имеющему ту же высоту, относятся, как размеры вертикального и наклонного пути:
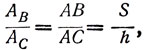
где Ас и Ав - величины ускорения при движении соответственно по АС и АВ. В самом деле, скорость при равноускоренном движении связана с ускорением и пройденным путём следующим выражением:
(4)
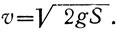
В данном случае для скоростей в конце пути по АВ АС можно написать:
(5)
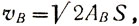
(6)
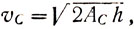
но υB = υc И AC = g, следовательно:
(7)
AB · S = g · h,
или
(8)

где α - угол наклонной плоскости с горизонталью.
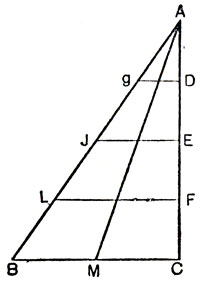
Рис. 8
Теперь легко доказывается и утверждение "г". Галилей строит для этого чертёж, приведённый на рисунке 8. Ход его рассуждений следующий: на основании предыдущего следует, что скорости в С,М, В одинаковы, так же они будут одинаковы и для любой промежуточной горизонтали gDJE,LF. Следовательно, на любых участках, ограниченных двумя параллельными линиями, будет иметь место один и тот же прирост скорости. Отсюда доказывается, что в этом случае отношение пройденных расстояний равно отношению промежутков времени, откуда следует утверждение, сформулированное в пункте "г":
(9)
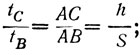
алгебраически это доказывается так:
(10)
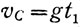
и соответственно:
(11)υB = υC
но для заданных условий пользуясь же уравнением 8:
(12)
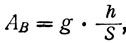
и следовательно:
(13)
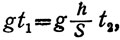
откуда:
(14)
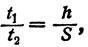
что и требовалось доказать.
Так же переводится на алгебраический язык доказа тельство утверждения "д" (см. рис. 9):
(15)
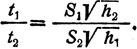
В самом деле, из уравнения 14 следует, что время движения по плоскости S1 равно:
(16)
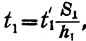
где t1 - время свободного падения по h1 в свою очередь равно:
(17)
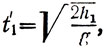
откуда
(18)
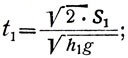
аналогично можем написать:
(19)

разделив уравнение 18 на уравнение 19, получим уравнение 15, которое и следовало доказать.
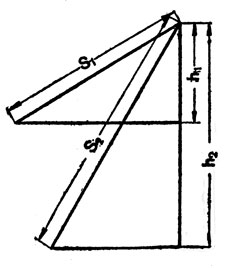
Рис. 9
Утверждения "е" и "ж" приведены здесь для иллюстрации того, что чисто геометрические построения становились громоздкими для решения ряда механических задач. С учётом профиля данной книги эти утверждения приведены также для того, чтобы при желании использовать для самостоятельного доказательства их справедливости современными методами.
Несколько особо стоит утверждение "з", поскольку оно впервые рассматривает случай падения тел по наклонной плоскости с начальными скоростями, отличными от нуля. При геометрических построениях доказательство этого утверждения очень наглядно. Доказательство Галилея сводится к тому, что треугольник интервалов времени для прохождения путей по двум плоскостям, меняясь по величине, остаётся всегда подобен одному и тому же треугольнику, вне зависимости от того, с какой начальной скоростью начато движение.
Алгебраически это доказывается так. В общем виде мы можем написать для обеих наклонных плоскостей:
(20)
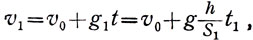
(21)
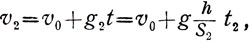
но при равных высотах каждая из этих скоростей порознь равна скорости движения по вертикали:
(22)
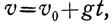
откуда
(23)
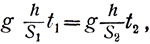
или, даже в этом общем случае, сохраняется зависимость:
(24)
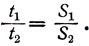
Заключение
Галилей, изучая законы движения тела по наклонной плоскости, показал, что в этом случае также сохраняется равноускоренное движение, но ускорение здесь меньше ускорения при свободном падении (движение по вертикали) и изменяется прямо пропорционально наклону плоскости, по которой падает тело.
Кроме того, он показал, каким образом определяется время падения как с начала движения, так и на любом отрезке пути. Галилей доказал также, что скорость, которой достигнет тело, зависит лишь от высоты по вертикали, но не зависит от наклона, по которому происходит падение.
Вне этого круга вопросов Галилей наклонной плоскостью не занимался, оставив в стороне вопросы соотношения сил и скоростей.
Иначе говоря, его интересовал вопрос изменения скоростей за счёт изменения наклона плоскости, но он не занимался вопросом зависимости сил, действующих на тело, находящееся на наклонной плоскости, от угла наклона.
|
ПОИСК:
|