Тема четвёртая: Движение тела, брошенного под углом к горизонту

("Беседы": а) стр. 418; б) стр. 464; в) стр. 467; г) стр. 472 - 473.)

а) При сложном движении, слагающемся из равномерного горизонтального и естественно ускоренного движений, бросаемое тело описывает полупараболу.

г) Импульс или момент в конечной точке полупараболы равняется моменту естественного падения по вертикали с высоты, равной сумме сублимита и высоте полупараболы.

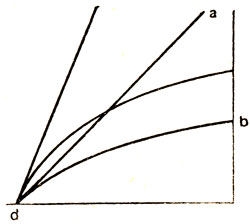
Рис. 10

Отсюда вытекает, что импульсы движения по всем полупараболам, суммы высот и сублимитов которых равны между собой, одинаковы.

Пожалуй, ни по одному из вопросов механики Галилей не сделал большего, не проник так глубоко в сущность процесса, как в области изучения законов движения тела, брошенного под углом к горизонту.

Леонардо да Винчи и Тарталья отрицали старую, неправильную качественную картину движения брошенного тела и противопоставили ей другую, более правильную, но тоже качественную картину.

Галилей существенно развил теорию этого вопроса. Он доказал, что формой движения тела в пространстве является парабола, и сделал ряд выводов из этого. Это не только подведение количественной базы под сущность процесса, - это новая методика изучения вопроса.

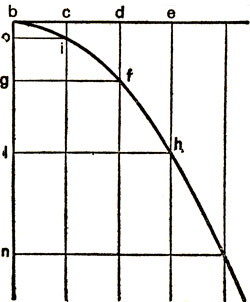
Рис. 11

В утверждении, приведённом в пункте "а", Галилей для упрощения начинает со случая, когда тело брошено параллельно горизонту. Доказательство этого утверждения настолько характерно для методики,Галилея, что оно приводится здесь полностью:

"Представим себе высоко расположенную горизонтальную линию или плоскость ab, между точками которой а и b (см. рис. 11) равномерно движется тело: за отсутствием дальнейшей поддержки со стороны плоскости тело будет стремиться, вследствие своей тяжести, двигаться от точки b как естественно падающее вдоль вертикали bп. Предположим, что плоскость ab продолжена на расстояние bc, которое будет служить для измерения времени, и отложим на этой последней линии произвольные, но равные части bc, cd, de, со-ответствующие каким-либо равным промежуткам времени. Проведем через точки b, с, d, e линии, параллельные вертикали bп, а затем отложим на первой из этих линий произвольный отрезок ci, на сле-дующей - в четыре раза больший отрезок df, на третьей в девять раз больший отрезок eh1, так что указанные отрезки будут относиться между собой, как квадраты линий cb, db, eb. Если мы представим себе теперь, что к равномерному движению тела от b до с присоединяется падение по вертикали на величину ci, то через промежуток времени bc оно будет находиться в точке i. Рассуждая таким же образом, найдём, что через промежуток времени db, равный удвоенному dc, тело упадёт на расстояние, в четыре раза большее первоначального ci, ибо, как уже было доказано в первом трактате, расстояния, проходимые телами при естественно ускоренном движении, относятся между собой, как квадраты времён падения. Подобным же образом находим, что пространство ch, пройденное за время be, равняется девяти ci и что вообще пространства eh, df, ci относятся между собой, как квад-раты линий еb, db, cb. Проведём через точки i, f, h прямые линии io, fg, hl, параллельные eb. Линии hl, fg, io будут соответственно равны линиям eb, db, cb; равным образом и линии bo, bg, bl будут соответственно равны линиям ci, df, eh. Поэтому отношение квадрата hi к квадрату fg будет равно отношению линии eb к bg, a отношение квадрата fg к квадрату iо равно отношению линии gb к bo; следовательно, точки i, f и h расположены на параболе. Взяв любые другие равные отрезки, соответствующие времени движения тела, можно подобным же образом доказать, что все места, занимаемые телом при таком сложном движении, лежат на параболической линии; следовательно, предположение доказано".

Если это доказательство перевести на язык алгебры, то оно будет иметь следующий вид. Движение тела, выброшенного параллельно горизонту, будет результатом сложения двух движений: одного - равномерного, с постоянной скоростью, определяемой начальной скоростью выброса тела:

(1) υ₁ = υ₀

и другого - равноускоренного, определяемого силой тяжести:

(2) υ₂ = gt.

Если начало координат поместить в точку b (см. рис. 11) и для сохранения вида этого рисунка ось х направить по bc, а ось y по bn, то предыдущие уравнения могут быть переписаны в виде:

(3)

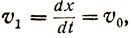
откуда

(4)

(5)

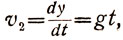
следовательно:

(6)

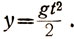
Для получения уравнения параболы надо найти взаимную связь между у и х. Для этого решим уравнение 4 относительно t и подставим это решение в уравнение 6, тогда получим уравнение траектории движения, в которое время уже входить не будет:

(7)

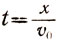
(8)

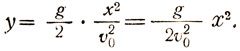
Последнее выражение и является уравнением параболы движения

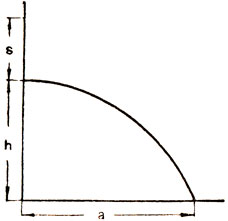
Рис. 12

Перейдём к рассмотрению утверждения, приведённого в пункте "б"^*. Мы не будем здесь приводить геометрического доказательства этого утверждения в том виде, как оно дано Галилеем, Укажем лишь, что это доказательство построено на том, что конечная скорость движения рассматривается как диагональ прямоугольника, составленного из горизонтальной и вертикальной скоростей. В процессе доказательства выводится, что эта диагональ будет наименьшей при заданных условиях a=2h и станет диагональю квадрата Отход от этого оптимального соотношения приводит к прямоугольнику скоростей. В одну сторону - с меньшей горизонтальной стороной, в другую - с меньшей вертикальной стороной. Алгебраически это доказательство может быть проведено следующим образом.

^* (Для однозначного понимания терминов, употребляемых Галилеем, укажем, что ас называется им высотой, или осью, параболы, cв - амплитудой и еа - сублимитом. (Высота, при которой за счёт свободного падения приобретается скорость, равная начальной скорости по оси х и обозначенная выше - υ₀). Понятие "сублимит" Галилей специально ввёл для своих геометрических построений. Мы будем обозначать далее высоту h и амплитуду а.)

Зависимость между амплитудой и высотой на основе уравнения 8 найдётся в виде:

(9)

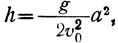
и следовательно, горизонтальная составляющая скорости будет связана с h и а уравнением:

(10)

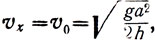
вертикальная же составляющая скорости определится из выражения:

(11)

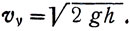
Суммарная скорость в месте приземления (или импульс, по терминологии Галилея) найдётся как геометрическая сумма скоростей vх и vv.

(12)

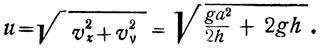
Отсюда можно найти, что минимальным будет выражение для и при а = 2h.

Очень характерным для методики Галилея является приём, которым он пользуется для перехода от случая тела, брошенного горизонтально, к случаю, когда тело брошено под углом к горизонту Любую параболу падения можно рассматривать как параболу подъёма, если сохранить связанными следующие соотношения: если при неизменных h и а тело выбросить со скоростью

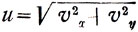
под тем же углом, который имеет к горизонту касательная в месте приземления, то параболы движения будут идентичны для падения с начальной скоростью υ₀ или подъёма с начальной скоростью и и соответствующим углом.

Таким образом, Галилею было очень легко доказать, что так как гипотенуза и при соотношении а = 2h строится на сторонах квадрата, то угол её к горизонту будет равен половине прямого (45°).

Алгебраически это докажется так: скорость υ_y = √2gh (см. уравнение 11), скорость

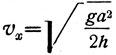
(см. уравнение 10).

При оптимальных условиях а = 2h. Подставим это в последнее выражение:

(13)

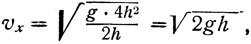
т. е. при оптимальных условиях υ_x = υ_y и начальная скорость и должна быть направлена под углом 45° к горизонту.

Очень своеобразно утверждение "г". На первый взгляд оно кажется даже неправильным. Как может простая сумма любых отрезков соответствовать одной и той же конечной скорости, находящейся в квадратичной зависимости от этих отрезков. Однако справедливость этого утверждения Галилея легко доказать.

Скорость υ_х в зависимости от высоты сублимита S можно написать в виде:

(14)

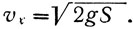
Для скорости же vv можем написать (см. уравнение 11):

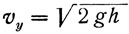
тогда

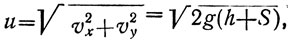
т. е. конечная скорость и (импульс, или момент в терминологии Галилея) зависит лишь от суммы высоты параболы и сублимита.

Галилей показал, что тело, брошенное под углом к горизонту, будет лететь по параболе. Он дал метод расчёта траекторий движения тела для любых углов вылета и для любых начальных скоростей. На основании этого он вычислил таблицы для артиллерийской стрельбы. Он показал, что наиболее эффективное использование начального импульса будет при выбросе тела под углом 45° к горизонту.

Он впервые использовал геометрическое сложение скоростей, т, е. приблизился к векторальному представлению о скорости.