Тема пятая: Теория маятника

^* ("Беседы"; а) стр. 175 - 176; г) стр, 175 - 176; д) стр. 194. ""Диалоги"; б) стр. 318; в) стр. 177.)

а) Опыты с двумя телами, возможно больше отличающимися друг от друга по весу, которые мы заставляем падать с некоторой высоты, наблюдая, перемещаются ли они с одинаковой скоростью, представляют некоторые трудности.

в) Самая нить представляет собой сочетание многих тяжёлых маятников, прикреплённых всё ближе и ближе к точке А.

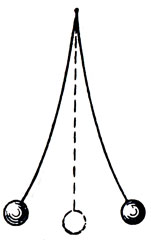
Рис 13

Наблюдая за нитью АС (см. рис. 13), мы увидим её направленной не прямо, а дугой. И если мы возьмём вместо нити цепь, то увидим это явление особенно наглядно... ибо, поскольку цепь состоит из многих сцепленных звеньев, а каждое из них довольно тяжело, дуги ЛЕС и AFD окаоюутся заметно искривлёнными.

д) Тела, опускающиеся по дугам, соответствующим хордам, наклонным к горизонту и не превышающим четверти круга, совершают движение, как показывает опыт, также в равные промежутки времени и притом меньшие, нежели при движении по хордам, - явление тем более удивительное, что можно было бы ожидать как раз противоположного.

В утверждении "а" Галилей сам рассказывает, почему он заинтересовался колебаниями маятника. Перед ним стояла задача экспериментально проверить сравнительную скорость падения тел разного веса, чтобы убедиться самому и доказать другим, что вес тела не влияет на скорость падения.

Некоторые биографы Галилея говорят, что он взбирался для этого на вершину знаменитой "падающей" Пизанской башни. Но как точно сравнить время падения, если оно для такой высоты занимает время немногим более секунды. Галилей открыл, что можно использовать наклонную плоскость для замедления процессов падения, без искажения самого характера равноускоренного движения. Такой опыт, очень интересовавший самого Галилея, был, однако, недостаточно нагляден, чтобы заставить признать правоту выводов Галилея его противниками.

Маятники, у которых степень отставания одного от другого может всё время наращиваться, по мысли Галилея, и должны были явиться удобными для наглядного доказательства независимости скорости падения от веса тела.

Галилей брал одинакового размера шарики из свинца и пробки^*, подвешенные на нитях одинаковой длины, и показывал, что их качание происходит совершенно одинаково, несмотря на существенное отличие в весе обоих шариков.

^* (Галилей понимал, как мы увидим в шестой теме, влияние трения на колебания маятника и ему была ясна поэтому необходимость максимально возможной идентичности размеров шариков.)

Гюйгенс, во второй половине XVII в., впервые вывел уравнение для определения периода качания маятника, у которого можно пренебречь влиянием массы нити, в виде:

(1)

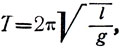
где l - длина веса подвеса,

g - ускорение силы тяжести.

Галилей ещё не знал этой зависимости, но он понимал, как мы видим из утверждения "б", что период колебания маятника зависит лишь от длины нити, на которой подвешен груз. Он понимает также, что можно считать период колебаний независящим от амплитуды колебаний.

Разбирая влияние различных факторов на период качания маятника, Галилей в "Первом дне" "Бесед" говорит: "Что касается, далее, отношения времени качания тел, подвешенных к нитям различной длины, то промежутки времени относятся между собой, как корни квадратные из длин маятников, и обратно: длины маятников стоят между собой в двойной пропорции времён, т. е. относятся друг к другу как квадраты времён качания".

Если это утверждение записать алгебраическим языком, то оно будет иметь вид:

(2)

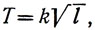
и следовательно, для полноты решения этой задачи Гали-лею не хватало знания того, что коэффициент пропорциональности между периодом качания Т и корнем квадратным из длины маятника зависит лишь от ускорения рилы тяжести и равен:

(3)

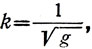
но для нахождения этой зависимости нужно было ввести энергетическую трактовку вопроса и иметь другой математический аппарат. Геометрические построения и пропорции здесь помочь Галилею не могли.

Из утверждения "в" следует, что Галилей понимал, правда, лишь качественно, как влияет масса подвеса, в том случае, если ею пренебречь нельзя. Он понимал, что реальная нить будет влиять на период качания маятника во всех случаях, но этим влиянием можно пренебречь, если масса нити будет значительно меньше, чем масса подвешенного к ней тела.

Галилей не знал ещё, что ускорение движения маятника происходит по закону:

(4) α = A · cos α,

где а - угол отклонения от вертикали, А - максимальное ускорение в крайнем нижнем положении.

Однако Галилей, как это следует из утверждения "г", понимал, что при движении по дуге окружности скорость не постоянна, и следовательно, движение не является равноускоренным. Как говорил Галилей: "ускорение нарастает по степеням", Галилей понимал также, что максимальное ускорение будет в нижнем положении маятника.

Очень характерным для оценки глубины проникновения Галилеем в существо процессов ускоренного движения тела является его утверждение, приведённое в пункте "д". Галилей доказал, что для спуска тела по наклонным линиям любой длины и наклона требуется одно и то же время, если эти наклонные линии являются хордами одной и той же окружности. Далее Галилей доказал, что это утверждение справедливо не только для хорд, но и для любых дуг, стягиваемых этими хордами, если эти дуги принадлежат одной окружности. Отсюда следует вывод Галилея о независимости периода качания маятника от амплитуды колебаний.

Галилей, однако, пошёл ещё дальше: он доказал, что время, потребное для падения по дуге, будет меньше, чем для движения по хорде, стягивающей эту дугу. Он правильно замечает при этом, что это "явление тем более удивительное, что можно было бы ожидать как раз противополооюного". Прямая, оказывается, не всегда является кратчайшим расстоянием при движении под действием силы тяжести.

Лишь в XVIII в. Лейбниц показал, что кратчайшим расстоянием для такого движения является циклоида, а при движении, зависящем от более сложных законов притяжения, такой кривой является брахистохрона. Это дало повод некоторым историкам утверждать, что утверждение Галилея, приведённое в пункте "д", является ошибочным. Такое заключение неверно. Галилей впервые правильно указал на возможность более короткого по времени пути по кривой, чем по прямой. Он не утверждал, что дуга окружности является кратчайшим расстоянием, а лишь более коротким, чем по наклонной прямой.

Галилей первым глубоко развил теорию маятника. Почти за сто лет до Гюйгенса он доказал, что период качания маятника зависит лишь от длины подвеса, если массой подвеса можно пренебречь по сравнению с массой качающегося тела.

Галилей доказал также, что период качания маятника не зависит от амплитуды его качания.

При помощи маятников Галилей очень наглядно показал неправильность утверждения Аристотеля, что скорость падения тела зависит от его веса.