
Тема девятая: Работы в области оптики и звука
Утверждения Галилея
("Беседы": а) стр. 199; б) стр. 203; в) стр. 204 - 205; г) стр. 204 - 205; д) стр. 113 - 114; е) стр. 113 - 114.)
а) Распространение колебательных движений в среде, окружающей звучащее тело, можно ясно наблюдать, заставив звучать кубок, частью налитый водою, водя концом пальца по его краю: содержащаяся в кубке вода покроется правильными волнами. Это явление наблюдается ещё отчётливее, если поставить ножку кубка на дно какого-нибудь достаточно широкого сосуда, наполнив последний водою почти до краёв кубка; заставляя трением пальца звучать кубок, мы увидим, как правильные волны побегут с большой быстротой по воде и соберутся на значительном расстоянии от кубка, заставляя звучать указанным способом достаточно большой кубок.
Я часто видел, как сперва образовывались с совершенной правильностью волны, затем звук стекла внезапно повышался на октаву и в тот же момент каждая из волн распадалась на две - явление, ясно указывающее, что форма октавы представляется двойной,
б) Я скоблил острым железным долотом пластинку из латуни, чтобы удалить с неё пятна, и при быстром много кратном движении долота раз или два услышал ясный и чистый звук; когда я посмотрел на пластинку, то увидел длинные ряды тончайших пылинок, расположенных параллельно и на совершенно одинаковом расстоянии.
При более высоких тонах штрихи получались болев сближенными, а при низких - более редкими.
в) Из двух струн... одна струна должна быть в четыре раза толще другой, чтобы разница в тоне равнялась октаве.
Если я хочу получить октаву из струн - одной латунной, а другой жильной, - то нет надобности, чтобы одна была в четыре раза толще другой; необходимо только, чтобы одна была в четыре раза тяжелее другой.
г) Ближайшая и непосредственная причина формы музыкальных интервалов лежит не в длине струны и не в толщине или степени натяжения: она заключается в отношении между числами колебаний и ударов воздушных волн, доходящих до барабанной перепонки нашего уха и заставляющих её дрожать с соответственной скоростью.
д) Два компаньона помещаются вместе со своими огнями в расстоянии двух или трёх миль друг от друга и, выждав ночи для производства опыта, начинают внимательно наблюдать, получается ли ответ на открытие и закрытие огня с тою же быстротою, что и на близком расстоянии; если получается, то можно с достоверностью за ключить, что распространение света происходит мгновенно.
е) Мне удалось провести его (опыт) лишь на малом расстоянии - менее одной мили, - почему я и не мог убедиться, действительно ли появление противоположного света совершается внезапно. Но если оно и происходит не внезапно, то, во всяком случае, с чрезвычайной быстро той, почти мгновенно.
Разбор утверждений
Как уже указывалось ранее, работы Галилея в области акустики, положившие вместе с работами Леонардо да Винчи начало этому разделу физики, охватывали широкий круг вопросов.
В этих работах изучалась связь между субъективным ощущением и частотой колебаний, был разработан метод оценки величины частоты колебаний по картине стоячих волн, производилось сравнение колебаний методом биений и был исследован ряд других тем. К ним примыкает такой вопрос, смежный между акустикой и механикой, как анализ факторов, определяющих величину частоты колебания струн.
Как это видно из утверждений "а" и "б", Галилей умел уже связывать протяжённость звуковой волны в пространстве с частотой колебаний, создающих эту волну. Он ещё не понимал, как связаны между собой длина волны, частота колебаний и скорость распространения, т. е. он не знал зависимости:
(1)
| λ= | c | |
| f |
где λ - длина волны, с - скорость распространения, f - частота колебаний.
Но он уже знал, что λ и f находятся в обратной пропорциональности. Несколько спорным является вопрос, понимал ли он величину длины волны в её движении, связанную с расстоянием между двумя сгущениями, или лишь как расстояние между видимыми полосами стоячих волн.
В пунктах "в" и "г" утверждений приведены основные представления Галилея о колебании струны. Современное решение задачи о колебании струн является одной из классических задач математической физики. Решается она методом дифференциальных уравнений в частных производных.
Галилей ещё не имел в своём распоряжении подобного математического аппарата. Он решал эту задачу на основе обобщения опытных данных, подкрепляя свои выводы геометрическими доказательствами.
Рассмотрим, насколько близки к современным представлениям его выводы, которые относятся к основному колебанию струны.
Уравнение для вычисления основной частоты этого колебания в настоящее время пишется в виде:
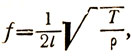
где f - величина основной частоты колебаний струны, l - длина струны, T - её натяжение, ρ - масса единицы длины струны.
В утверждении, приведённом в пункте "г", Галилей указывает, что на колебание струны влияет её длина, толщина и степень натяжения*.
* (Галилей указывает, что эти первичные причины не определяют физиологического воздействия звука; это воздействие определяется звуковыми волнами, возникающими вокруг струны и достигающими уха.)
Из этого видно, что Галилею были известны все фак торы, определяющие величину частоты колебания струны. Он понимал также, что между частотой и весом струны существует обратная квадратичная пропорциональность, т. е. он уже знал следующую частную зависимость уравнения 2:
| f | α | |
| √ρ |
Галилей не ограничивается этим; он показывает также понимание зависимости величины частоты от длины струны:
| f = β · | 1 | |
| l |
и от её натяжения:
f = γ · √T.
Свести всё это в одну формулу ему мешает приверженность к выражению зависимостей в виде пропорций и неумение использовать алгебраический язык для изложения своих выводов.
Выше уже отмечалось, что в области оптики Галилей сделал весьма мало. Описание опытов по установлению скорости света, вернее, даже решение вопроса о конечности этой скорости, приведённое в пунктах "д" и "г", показывает, что Галилей не представлял, насколько она может быть велика. Иначе он бы не ставил такого опыта. Пусть расстояние между двумя пунктами наблюдения измеряется десятками километров. Даже в этом случае время пробега световых волн в обе стороны будет равно десятым долям миллисекунды. Опаздывание рефлексов наблюдателей, как бы они ни были натренированы, введут ошибки, в тысячи раз большие, чем наблюдаемая величина.
Однако нельзя совсем отмахнуться от этих работ Галилея. Сама попытка поиска доказательств о конечности скорости света была для того времени очень смелым и прогрессивным шагом.
|
ПОИСК:
|