
Глава IV. Загадочная постоянная
В наши дни каждый школьник знает об электромагнитной природе световых волн. Однако очень долго электрические, магнитные и оптические явления считались относящимися к разным областям физики. В своем развитии оптика намного обогнала учение об электричестве - в начале XIX в., после появления работ Юнга, Френеля и других физиков-оптиков теория света получила прочное основание и считалась если не полностью завершенным, то, по крайней мере, вполне сложившимся разделом науки. Это же время для учения об электричестве и магнетизме - период интенсивного накопления экспериментальных фактов, которые еще предстояло обобщить в рамках единой теории.
На возможность существования связи между оптическими и электрическими явлениями ученые стали обращать внимание в середине XVIII в. Вероятно, первым указанием на такую связь было возникновение искры при электрическом разряде. Доказательство Б. Франклином (1706-1790) электрического происхождения молнии (1747 г.) подкрепило эту догадку. Великий русский ученый М. В. Ломоносов (1711-1765), занимавшийся как электрическими, так и оптическими исследованиями, предлагал проверить, будет ли луч света "иначе преломляться в наэлектризованном стекле и воде". В его "Химических и оптических записках" есть и такая заметка: "Отведать в фокусе зажигательного стекла или зеркала электрической силы". Неизвестно, пытался ли сам Ломоносов поставить предложенные им опыты. В начале XIX в. на возможную связь между оптическими и электрическими явлениями указывал Т. Юнг.
Важнейшим этапом в объединении оптических и электрических явлений стало открытие выдающегося английского физика Майкла Фарадея (1791-1867). В 1846 г. он обнаружил магнитооптический эффект, названный впоследствии его именем, который заключался во вращении плоскости поляризации света при прохождении через вещество, помещенное в магнитное поле. Световые волны, подобно волнам, распространяющимся в упругом резиновом шнуре, поперечны. Еще в 1816 г. Френель и Араго с помощью специальных опытов показали, что колебания в световой волне происходят в направлении, перпендикулярном направлению распространения волны. Фарадей установил, что если свет проходит через вещество, помещенное во внешнее магнитное поле, то плоскость, в которой происходят световые колебания, меняет свою ориентацию. Угол поворота плоскости зависит от величины индукции внешнего магнитного поля.
Размышления над обнаруженным явлением привели Фарадея к мысли о возможности существования электромагнитных волн и их связи со световыми волнами. Эта мысль намного опередила развитие науки. По ряду причин взгляды Фарадея не получили распространения вплоть до появления работ Максвелла, в которых была изложена теория электромагнитного поля.
К началу работы Максвелла над проблемами электромагнетизма физикам был известен экспериментальный факт, который, казалось бы, должен был привлечь всеобщее внимание к проблеме связи электрических и оптических явлений. Оказалось, что если выразить величину одного и того же заряда с помощью двух разных систем единиц, а затем найти отношение полученных значений, то это отношение, называемое электродинамической постоянной, будет иметь размерность скорости, а его величина оказывается близкой к скорости света. Однако большинство ученых считали этот факт непонятным физическим курьезом.
Такое отношение к результатам определения электродинамической постоянной нетрудно понять. Действительно, выбор той или иной системы единиц условен, поэтому сравнение единиц разных систем представляет лишь практический интерес. Стоит ли в связи с этим ставить какие-либо принципиальные вопросы?
Приведенное рассуждение не противоречит "здравому смыслу". Но, как это часто бывает в истории науки, ход ее развития показал ограниченность этой "естественной" точки зрения.
История электродинамической постоянной начинается во второй половине XVIII в. В то время ученые практически ничего не знали о связи между электрическими и магнитными явлениями, и эти явления изучались независимо друг от друга. Важнейшим этапом развития учения об электричестве явилось установление Ш. О. Кулоном (1785 г.) закона взаимодействия точечных зарядов. Найти же достаточно общий закон магнитных взаимодействий не удавалось. Лишь после того, как в 1820 г. X. Эрстед обнаружил магнитное действие тока, а А. Ампер установил закон взаимодействия токов, физики получили надежную основу для проведения количественных измерений в области магнетизма. Дальнейшие исследования подтвердили тесную связь между электрическими и магнитными явлениями. Особую роль в установлении этой связи сыграло открытие Фарадеем эффекта электромагнитной индукции (1831 г.).
Длительная "независимость" исследований электрических и магнитных явлений привела к важным для физики последствиям: возникли две системы единиц - электрическая и магнитная. Появление двух систем обусловлено общим подходом физиков к проблеме измерений или, иначе говоря, к метрологии. Подход этот состоит в том, что при обнаружении какого-либо неизвестного ранее свойства (например, способности заряженных тел отталкиваться или притягиваться) физики стараются ввести количественные характеристики, с помощью которых было бы удобно описывать эти свойства. При этом ставится условие: новые характеристики должны выражаться через ранее введенные физические величины. Поясним эту мысль на примере определения единицы измерения электрического заряда.
Кулон с помощью крутильных весов доказал, что сила взаимодействия между электрическими зарядами обратно пропорциональна квадрату расстояния между ними. Отметим, что задолго до Кулона к такому же выводу, обоснованному экспериментом, пришел английский физик и химик Г. Кавендиш. Однако метод, примененный Кавендишем, не позволял определить зависимость силы взаимодействия от величины зарядов, находящихся на телах, или, как говорили в XVIII в., от "количества электрического флюида". В связи с задачей нахождения "закона электрического отталкивания и притяжения" возникает интересная ситуация. Зависимость силы взаимодействия заряженных тел от величины сообщенных им зарядов можно установить, казалось бы, лишь зная величины зарядов. А как их можно определить? Опять же через силу взаимодействия между зарядами. Получается порочный круг. Главная заслуга Кулона состоит в том, что он нашел выход из этой, на первый взгляд безнадежной, ситуации. Кулон предложил следующую процедуру измерений. Сначала шарам крутильных весов сообщаются неизвестные заряды q1 и q2 и измеряется сила взаимодействия между шарами. Затем шар, не связанный с крутильным подвесом и обладающий зарядом q1, приводится в соприкосновение с точно таким же незаряженным шаром. Вследствие соприкосновения заряд q1 распределяется поровну между двумя шарами. (Этого можно ожидать из соображений симметрии, и, кроме того, равенство зарядов на одинаковых шарах можно проверить экспериментально.) Затем снова измеряется сила взаимодействия между шарами крутильных весов, которые теперь обладают зарядами q1/2 и q2. Такую процедуру можно продолжать и дальше. Если последовательно измеренные силы F1, F2, ... относятся как 1 : ½ : ¼, то можно сделать вывод о пропорциональности силы взаимодействия величинам зарядов, не зная их абсолютного значения. Не правда ли, красивая идея?
После установления закона Кулона стало ясно, как определить единицу количества электричества (единицу заряда), т. е. как выразить ее через известные величины. В конце XVIII в. наиболее развитой областью физики была механика, в которой основными единицами являются единицы времени, длины и массы. Через них определяется единица силы. Пользуясь законом Кулона
| F = K | q1q2 | , (IV. 1) |
| r2 |
можно определить единицу заряда следующим образом: единичным называется заряд, который взаимодействует с силой, равной единице, с равным себе и находящимся на единичном расстоянии зарядом. В зависимости от того, чему равен коэффициент К, получаются разные единицы заряда. Так, например, в современной системе CGSE К = 1, а в международной системе единиц (СИ) - K = 9⋅109, поэтому единицы заряда в двух системах связаны соотношением: 9⋅109 ед. заряда CGSE = 1 кулон.
Для введения единицы заряда можно использовать не только эффект электростатического взаимодействия, но и любое другое явление, зависящее от величины заряда. Поскольку электрический ток - это направленное движение заряженных частиц, величину заряда можно определить, рассматривая какое-либо явление, связанное с протеканием тока. То, какое явление будет выбрано, в конечном счете определит лишь удобство и точность измерений.
Открытие Эрстеда, а затем наблюдение взаимодействия двух проводов с током позволило ввести единицу силы тока. Однако независимое введение единиц тока и заряда с физической точки зрения бессмысленно. Здесь, правда, к выражению "с физической точки зрения" необходимо добавить еще и слово "современной". Дело в том, что эквивалентность двух родов электричества - статического и "гальванического"* была понята не сразу. Поэтому независимое введение двух тесно связанных между собой единиц измерения имеет историческое объяснение. Когда же физики поняли неудобство такого положения вещей, они попытались найти соотношение между единицей заряда, определенного на основе измерений магнитного действия тока, и единицей заряда, введенной с помощью электростатических измерений.
* ("Гальваническими" эффектами называются явления, обусловленные протеканием тока, вызванного действием сил неэлектростатического происхождения. Этот термин происходит от имени итальянского физиолога Л. Гальвани, впервые обнаружившего такие явления.)
Здесь мы, наконец, подошли к ответу на вопрос, который, по-видимому, давно волнует читателя: какое отношение имеет частная задача о связи двух единиц заряда к проблеме измерения скорости света?
Давайте определим размерность отношения Q/Q′ (Q - "электростатическая" единица заряда, a Q′ - единица заряда, введенная с помощью магнитных измерений).
Все единицы физических величин делятся на основные и производные. В СИ, например, к основным единицам относятся единицы длины, времени, массы и др. В этой же системе единица измерения скорости - производная, ее можно выразить через основные. Понятие размерности физической величины тесно связано с понятием единицы измерения, однако не совпадает с ним. Не рассматривая общего определения размерности, обсудим на примерах ее свойства.
Допустим, что в некоторой системе основными единицами измерений являются единицы длины (все величины, имеющие размерность длины, будем обозначать L), времени (Т) и массы (М). Скорость движения материальной точки v определяется соотношением v = Δs/Δt, где Δs - перемещение тела за время Δt. Ясно, что модуль перемещения |Δs| имеет размерность длины, поэтому размерность скорости
[V] = LT-1. (IV.2)
Может показаться, что сказанное выше - лишь облеченный в наукообразную форму всем известный факт, что скорость измеряется в сантиметрах в секунду, в метрах в секунду, в километрах в час и т. д. Однако в действительности введение понятия размерности физической величины вовсе не бесполезно. Соотношение (IV.2) отражает весьма общий факт, заключающийся в том, что если основными единицами измерения в некоторой системе являются единицы длины и времени, то размерность скорости всегда будет определяться соотношением (IV.2). При этом неважно, измеряется ли длина в километрах или нанометрах, а время - в часах или сутках - размерность скорости, в отличие от ее единицы измерения, не меняется.
Еще одно важное свойство размерности состоит в том, что размерность физической величины, единица измерения которой - производная, может зависеть от того, какое определяющее соотношение для нее выбрано. Поясним это на примере введения размерности силы. В использовавшейся нами системе единиц силу можно определить, исходя из второго закона Ньютона:
F = mа, т. е. [F] = MLT-2,
где [F] - размерность силы. Однако выбор второго закона Ньютона для определения [F] в значительной степени произволен. Мы могли бы для этого выбрать, например, закон всемирного тяготения, записанный в виде
| F = | m1m2 | , |
| r2 |
и тогда
[F] = M2 L-2!
Как же так? Одна и та же физическая величина в одной и той же системе единиц может иметь разную размерность? Не бессмыслица ли это?
Никакого логического противоречия в проведенном выше рассуждении нет. Возможность определения размерности одной и той же физической величины несколькими способами обусловлена весьма глубокими причинами, которые здесь нет возможности рассмотреть подробно*. Ясно, однако, что такое положение не слишком удобно. Чтобы упростить ситуацию, физики условились пользоваться для введения размерности производных величин строго определенными соотношениями. Так, в случае определения размерности силы предпочтение отдается второму закону Ньютона. Такой выбор приводит к появлению в законе всемирного тяготения размерной константы - гравитационной постоянной G:
| F = G | m1m2 | , |
| r2 |
* ( Отметим, что в рассмотренном примере важную роль играет эквивалентность инертной и гравитационной масс.)
только так можно добиться равенства размерностей силы в законе всемирного тяготения и во втором законе Ньютона. Как же определить размерность гравитационной постоянной? Это легко сделать, воспользовавшись принципом однородности физических величин, который утверждает, что одна и та же величина, входящая в выражения, отражающие разные законы физики, например, сила, должна иметь одну и ту же размерность. Выражением этого принципа является условное равенство
[G]M2L-2 = MLT-2, (IV.3)
т. е.
[G] = M-1L3T-2.
Вспомните, что в СИ, где единицы длины, времени, массы являются основными, G = 6,67⋅10-11 м3 ⋅ кг-1 ⋅ с-2.
Вернемся теперь к проблеме определения связи между двумя единицами заряда. Рассмотрим ее с точки зрения теории размерности. Пусть основными физическими величинами по-прежнему являются длина, время и масса. Какова в этом случае размерность величины электрического заряда, если в качестве определяющего соотношения использовать закон Кулона, записанный в виде
| F = | q1q2 | ? |
| r2 |
Очевидно, для нахождения размерности заряда [Q] следует воспользоваться равенством, подобным (IV.3): [F] = [Q]2L-2, или, переходя к основным величинам,
MLT-2 = [Q]2L-2.
Отсюда
[Q] = M1/2L3/2T-1.
Другой способ введения единицы заряда состоит в использовании закона Ампера, определяющего силу взаимодействия двух токов:
| F′ = | i1i2 | . (IV. 4) |
| r |
В формуле (IV. 4) опущен численный коэффициент, определяемый геометрией опыта. Здесь i1, i2 - токи во взаимодействующих проводниках, r - расстояние между проводниками. В формуле (IV.4) введено обозначение F′ - это сила, действующая на единицу длины проводника. Сила тока связана с величиной прошедшего по проводнику заряда известным соотношением i = q/t, следовательно, [I] = [Q′]T-1. Напомним, что штрих у буквы Q отражает тот факт, что единица заряда определяется через магнитное взаимодействие. Теперь можно найти [Q′]:
MT-2 = [Q′]2T-2L-1.
Отсюда
[Q′] = M1/2L1/2, (IV. 5)
Тот факт, что [Q′] ≠ [Q], не должен удивлять читателя: для нахождения [Q′] и [Q] были использованы разные определяющие соотношения. Найдем размерность отношения величин зарядов в электростатической системе [Q] и в электромагнитной системе [Q′]:
| [Q] | = LT-1. | |
| [Q′] |
Таким образом, искомое отношение имеет размерность скорости. Сам по себе этот факт вряд ли может привлечь внимание: в случае электростатических измерений взаимодействуют неподвижные заряды, а при магнитных измерениях - движущиеся. Стоит ли удивляться, что найденное отношение характеризуется размерностью скорости? Однако, какова величина этого отношения? Этот вопрос и заинтересовал немецкого ученого Вильгельма Вебера, который первым из физиков попытался ответить на него с помощью опыта.

Вильгельм Вебер (1804-1891)
В середине XIX в. Вебер (1804-1891) был заметной фигурой в научном мире. Он родился в семье профессора теологии Виттенбергского университета. Уважение к науке в семье Веберов было огромным. Вследствие этого из четырех братьев трое стали учеными, и Вильгельм - самым известным из них. Уже с тринадцати лет он принимал участие в опытах по изучению волн на воде и в воздухе, проводившихся старшим братом. В 1822 г. Вебер поступил в университет г. Галле, где получил хорошую подготовку по физике и математике. После окончания университета Вебер начал вести самостоятельные научные исследования. В 1828 г. молодой ученый принял участие в работе Съезда немецких естествоиспытателей и врачей в Берлине. Его доклад об органных трубах, прочитанный на Съезде, привлек внимание "короля математиков" - К. Ф. Гаусса (1777-1855). В это время Гаусс под влиянием выдающегося немецкого естествоиспытателя А. Гумбольдта увлекся проблемой изучения магнитного поля Земли. Для осуществления задуманной Гауссом и Гумбольдтом огромной программы по исследованию геомагнетизма требовался знающий сотрудник. Гаусс предложил Веберу совместную работу.
Сотрудничество Гаусса и Вебер а началось в 1831 г., когда Вебер получил кафедру физики в Геттингене - городе, где работал Гаусс. Их совместная работа продолжалась шесть лет, которые составили эпоху в развитии не только геофизических измерений, но и электромагнитных измерений вообще.
Вебер не открыл ни одного нового физического явления в области электромагнетизма. В этом смысле его творчество резко контрастирует с работами Фарадея. Однако, в отличие от Фарадея, опыты которого были в основном качественными, Вебер стремился внести в электромагнитные исследования точность и однозначность, присущие механическим измерениям. Основная идея, которую развивали Вебер и Гаусс, состояла в том, чтобы свести электрические и магнитные измерения к механическим и, таким образом, выразить электромагнитные величины через единицы времени, длины, массы. Эту идею Вебер стремился реализовать, конструируя чувствительные магнитометры и другие приборы. Увлечение метрологией явилось одной из причин интереса Вебера к определению электродинамической постоянной. В целом геомагнитные работы Вебера и Гаусса подняли технику измерений на качественно новый уровень.
Совместная работа Вебера и Гаусса была прервана вследствие событий, не имеющих отношения к науке. В 1837 г. после смерти короля Вильгельма IV в Ганноверском государстве, к которому относился Геттинген, была отменена либеральная конституция. Вебер в числе семи профессоров университета подал правительству протест. За этот смелый шаг ученые дорого поплатились - они были отстранены от должности. Не помогло даже вмешательство таких влиятельных людей, как Гумбольдт и Гаусс.
Вебер уехал из Геттингена. В 1843 г. ему удалось получить кафедру физики в Лейпциге. Здесь ученый провел важные теоретические исследования в области электричества и магнетизма. Итогом этих исследований стал закон действия "электрических сил", предложенный Вебером в 1846 г.
Ученый поставил своей целью объединить в одной формуле электростатическое и магнитное взаимодействия зарядов, а также описать явление электромагнитной индукции. Стремление решить столь общую задачу привело к тому, что вид веберовского закона взаимодействия электрических зарядов оказался весьма необычным: в выражение для силы входят слагаемые, зависящие не только от величины взаимодействующих зарядов и расстояния между ними, но и от их относительной скорости и даже от ускорения! Следует отметить, что в формуле Вебера фигурировала в качестве константы уже знакомая нам электродинамическая постоянная. Ее определение представляло для автора теории значительный интерес.
Так определение электродинамической постоянной оказалось точкой пересечения двух, казалось бы, противоречащих друг другу увлечений Вебера: метрологии и теоретических исследований в области электромагнетизма. Вебер поставил эксперимент вместе со своим сотрудником Рудольфом Кольраушем (1809-1858). Задачу исследователи формулировали следующим образом:
"Пусть дан постоянный ток, поддерживающий в равновесии тангенс-буссоль с простым мультипликаторным контуром радиуса R мм при отклонении
| φ = arctg | 2π | , | |
| Rτ |
где τ обозначает силу отклоняющего буссоль горизонтального земного магнетизма. Требуется определить, как относится количество электричества, проходящее при таком токе за одну секунду через поперечное сечение проводника, к количеству электричества на каждом из двух одинаково заряженных бесконечно малых шариков, отталкивающихся друг от друга с единицей силы на расстоянии в один миллиметр. При этом за единицу силы принимается сила, сообщающая массе в 1 миллиграмм в течение 1 секунды прирост скорости на 1 миллиметр".

Рудольф Кольрауш (1809-1858)
Несмотря на незнакомые многим читателям слова в первой фразе, идея задачи очень проста: сравнить заряд, проходящий через поперечное сечение проводника в единицу времени при токе заданной величины (первая фраза определяет силу тока: по существу, тангенс-буссоль - это своеобразный амперметр, а величина φ - отклонение его стрелки), с зарядом, величина которого определяется по электростатическому взаимодействию.
Опыт проводился так. Сначала определялись относительные емкости небольшой лейденской банки (конденсатора) и покрытого станиолем шара. Таким образом, распределение заряда между банкой и шаром, которое устанавливается, если одну из обкладок банки соединить с шаром, было известно.
Лейденская банка сперва полностью разряжалась. После этого заряженный большой шар приводился в соприкосновение с одной из обкладок банки, затем эта связь прерывалась. Заряд, перешедший на обкладку банки, разряжался через мультипликатор (обмотку), имевший 5635 витков. Протекание тока через обмотку вызывало отклонение магнитной стрелки. Это отклонение регистрировалось с возможно большей точностью. В это же время большой шар, сохранивший известную долю своего заряда, приводился в соприкосновение с неподвижным шаром крутильных весов (подобных крутильным весам Кулона - Кавендиша). Поскольку размеры шаров были известны, можно было определить, какая часть заряда перешла с большого шара на шар крутильных весов. Затем, будучи вложен в ящик весов, шар отдавал половину своего заряда подвижному шару тех же размеров; вслед за этим измерялось закручивание нити весов. Последнее измерение позволяло определить абсолютную величину заряда, первоначально находившегося на большом шаре, в электростатических единицах. Из измерения отклонения магнитной стрелки в первой части опыта можно было найти эту же величину в магнитных единицах.
Если перевести полученные Вебером и Кольраушем результаты в современные единицы измерения, то среднее значение искомого отношения окажется равным 310740 км/с.
Казалось бы, полученный результат должен был заставить Вебера и Кольрауша задуматься о причинах; близости величины электромагнитной постоянной и скорости света. Действительно, ведь сам Вебер еще в 1846 г. в работе, где был сформулирован его закон взаимодействия электрических зарядов, писал:
"...мне необходимо лишь напомнить о новейшем открытии Фарадеем воздействия электрического тока на распространение световых колебаний*, которое делает не неправдоподобным предположение о том, что всюду проникающая нейтральная электрическая среда и является тем всепроникающим эфиром, который создает и передает световые колебания, или, по крайней мере, что они оба так тесно связаны друг с другом, что наблюдение распространения света может дать объяснение действию электрической нейтральной среды".
* (Речь идет об открытии явления вращения плоскости поляризации света при прохождении через вещество, помещенное в магнитное поле (см. с. 72).)
В этих словах можно усмотреть догадку об электромагнитной природе света. И все же приходится констатировать, что ни Вебер, ни Кольрауш не пришли к каким-либо выводам относительно полученного ими результата. Возможно, им помешало убеждение в справедливости теории Вебера.
Эта теория была развитием электродинамики Ампера. В ней сохранилась главная идея Ампера - идея дальнодействия. Во всех теориях, основывающихся на принципе дальнодействия, сила взаимодействия между телами, будь то сила гравитационного притяжения в законе всемирного тяготения или кулоновская сила, действующая между зарядами, зависит только от расстояния между ними. Вследствие этого оказывается, что при изменении этого расстояния сила взаимодействия должна измениться мгновенно, как бы далеко ни были разнесены тела. Хотя в связи с принципом дальнодействия возникают некоторые острые вопросы методологического характера, т. е. связанные с методом научного познания, соответствующие теории вполне удовлетворительно описывают физические явления, когда рассматриваются задачи статики или когда относительная скорость взаимодействующих объектов мала. Здесь вполне уместен вопрос: каков критерий для определения того, мала или велика эта скорость? С чем ее сравнить? Теперь мы хорошо знаем ответ, а во времена Вебера такой критерий отсутствовал, и большинство ученых считали дальнодействие абсолютным принципом физики. Этим, по-видимому, и объясняется "безразличие" Вебера к собственным результатам: в рамках теории дальнодействия нет места каким бы то ни было универсальным скоростям - взаимодействие осуществляется мгновенно!
Итак, результат, полученный Вебером и Кольраушем, вынужден был дожидаться правильного объяснения. Его интерпретация невозможна без ясного понимания механизма передачи взаимодействия. Это, по-видимому, сознавали многие физики, работавшие в середине XIX в. И хотя формально теория дальнодействующих электромагнитных сил Вебера не сталкивалась со сколько-нибудь серьезной оппозицией, подспудно зрели идеи близкодействия, важнейшим следствием которых является конечность скорости распространения взаимодействий.
Однако для пересмотра господствовавших в то время воззрений требовалась новая фундаментальная идея. Эта идея сформировалась в работах Фарадея, который предположил, что существует особый физический объект - электромагнитное поле.
История формирования идеи Фарадея об электромагнитном поле - интереснейшая страница истории науки. Здесь мы вынуждены ограничиться лишь весьма краткими сведениями о том, как ученый пришел к мысли о поле.
Важнейшей особенностью творчества Фарадея является удивительное сочетание тонкого экспериментального искусства и умения проводить обобщение результатов опытов без использования каких бы то ни было математических методов. Одним из первых результатов метода Фарадея было предположение о реальном существовании силовых линий, тянущихся непрерывно от одного заряженного тела к другому. Сама мысль о силовых линиях высказывалась учеными и до Фарадея, однако лишь в его работах они стали рассматриваться как истинные носители физических взаимодействий. Согласно Фарадею, все тела окружены силовыми линиями разной природы (электрическими, магнитными и т. д.); эффект присутствия заряженного тела сводится не только к возникновению силы, действующей на другое заряженное тело, но и к изменению физических свойств пространства вокруг первого тела. К этой мысли Фарадей шел долго, но тем более плодотворными были ее следствия. Одно из них состояло в том, что световые колебания могут быть обусловлены колебаниями силовых линий.
Ученый мир познакомился с точкой зрения Фарадея на природу света в 1846 г., после того как Фарадей выступил на семинаре, заполняя время, оставшееся после чтения работы Уитстона; некоторое время спустя работа Фарадея была опубликована в форме письма к его другу и сотруднику Филлипсу. Приведем отрывок из этого письма:
"Какой бы точки зрения на силовые линии ни держаться, мы во всяком случае можем действовать на них некоторым способом, который мы можем представить себе как имеющий характер сотрясения или бокового колебания. В самом деле, вообразим себе, что два тела А и В находятся на некотором расстоянии друг от друга и взаимодействуют друг с другом, а следовательно, связаны силовыми линиями; обратим внимание на какую-нибудь одну результирующую силы, имеющую неизменное направление по отношению к пространству. Если одно из тел хотя в самой малой степени сдвинется вправо или влево или если его сила переместится на мгновение внутри массы (а это легко себе представить, если А и В - электрические или магнитные тела), то в результирующей силе, на которой мы сосредоточили свое внимание, произойдет изменение, эквивалентное боковому возмущению. Действительно, ее интенсивность должна или возрасти, если интенсивность соседних результирующих уменьшится, или уменьшиться, если последняя увеличится...
Точка зрения, которую я имею смелость предложить, рассматривает, таким образом, излучение, как колебания высокого порядка в силовых линиях, которые, как известно, соединяют друг с другом частицы и тем самым материальные массы".
Однако мысли о происхождении излучения, иллюстрируемые приведенным отрывком, не получили отклика в среде физиков. Причины равнодушного отношения к блестящим идеям английского ученого связаны, отчасти, с его методом исследования. С формальной точки зрения позиции сторонников дальнодействия представлялись значительно более прочными, чем рассуждения Фарадея. На стороне дальнодействия была вся мощь развитого к тому времени математического аппарата, а на стороне Фарадея - только более или менее интересные аналогии. Именно поэтому огромное уважение к экспериментальному гению Фарадея соседствовало с презрением к его теоретическим воззрениям. Для распространения идей Фарадея необходимо было перевести их на язык математики. Эта задача была решена Джеймсом Клерком Максвеллом.
Максвелл родился 13 июня 1831 г. в Эдинбурге в семье юриста, живо интересовавшегося проблемами: науки и техники. С ранних лет мальчик отличался наблюдательностью и пытливостью ума. Свою первую научную работу Максвелл написал в возрасте четырнадцати лет. Учился будущий создатель электромагнитной теории сначала в Эдинбургской академии (средней школе), затем в Эдинбургском университете. Примерно: через три года после начала учебы в университете Джеймс перешел в Кембриджский университет, славившийся своими традициями в преподавании физики и математики. Максвелл был одним из лучших студентов своего выпуска; после окончания учебы он стал преподавателем Тринити-колледжа в Кембридже.
Знакомство с биографией Максвелла показывает, что он довольно часто переезжал с одного места на другое, меняя должности и круг обязанностей. После Тринити-колледжа он преподавал в Маришаль-колледже в шотландском городе Абердине и в Королевском колледже в Лондоне. С 1865 г. по 1871 г. Максвелл уединенно жил в своем родовом поместье в Шотландии и не занимал никакого официального поста. Последние восемь лет жизни он возглавлял первую в истории Кембриджского университета кафедру экспериментальной физики. Максвеллу история науки обязана созданием выдающегося центра физических исследований - Кавендишской лаборатории.
Одно обстоятельство оставалось неизменным в течение всей жизни Максвелла - постоянный труд над важнейшими проблемами физики. Ученый прожил всего 48 лет (Максвелл умер в 1879 г.), но оставил после себя уникальное по разнообразию и глубине научное наследство. Он добился успеха в разгадке строения колец Сатурна и провел глубокие исследования по теории цветового зрения, его по праву считают одним из основателей статистической физики и термодинамики. Однако наиболее значительным в творчестве Максвелла представляется его теория электромагнитного поля.
Для создания единой теории электромагнетизма необходимо было слияние в одном ученом двух качеств: острой интуиции, характерной для выдающихся экспериментаторов, и математического таланта, присущего теоретику. Этими дополняющими друг друга качествами в полной мере обладал Максвелл. Это, по-видимому, понял еще Фарадей. Он писал двадцатишестилетнему Максвеллу:
"...Мне очень хотелось бы задать Вам один вопрос. Предположим, математик занимается исследованием физического явления и приходит, наконец, к каким-то определенным выводам. Нельзя ли их выразить в общедоступной форме не менее полно, ясно и конкретно, чем с помощью математических формул? Если можно, то для таких, как я, было бы великим благом получить их переведенными с языка иероглифов, так чтобы мы могли оперировать ими в процессе эксперимента. Я думаю, что это можно сделать, поскольку идея Ваших выводов мне совершенно ясна, хотя я и не всегда могу проследить в деталях за ходом Ваших рассуждений. Результаты, полученные на основании Ваших формул, неизменно лежат не выше и не ниже истинных, и смысл их вполне очевиден, так что я могу работать с ними".
Письмо Фарадея было написано после выхода в свет работы Максвелла "О фарадеевских силовых линиях", в которой ученому удалось выразить на языке математики некоторые идеи Фарадея. В 1860-1865 гг. Максвелл упорно работал над созданием полной математической теории электромагнитных явлений. Эта теория основывалась на представлении о поле - новом физическом объекте, введение которого позволило отказаться от дальнодействующих сил. В соответствии с теорией Максвелла взаимодействие между телами происходит благодаря полю, окружающему заряды и токи; изменение взаимодействия (например, вследствие смещения зарядов) возможно лишь при изменении поля, передающемся из одной точки пространства в другую с конечной скоростью. Важнейший вывод теории Максвелла - существование электромагнитных волн, которые могут распространяться в пространстве, свободном от вещества, со скоростью, равной ... электродинамической постоянной из закона Вебера! Теория Максвелла не только установила физический смысл этой постоянной, она связала две области, казавшиеся ранее очень далекими, - электромагнетизм и оптику.
Работа Максвелла, в которой впервые в достаточно полной форме была изложена его теория, называлась "Динамическая теория электромагнитного поля". Она была опубликована в 1864 г. Для нашей истории наибольший интерес представляет часть VI этой работы: "Электромагнитная теория света". В ней, исходя из основных уравнений теории, Максвелл получил уравнение для электромагнитной волны и нашел выражение для ее скорости υ*. Далее он писал:
* (В дальнейшем изложении используются упрощенные обозначения, не соответствующие в точности принятым у Максвелла. Объяснения Максвелла цитируются точно.)
"Эта волна состоит полностью из магнитных возмущений... Отсюда магнитные возмущения, распространяющиеся через электромагнитное поле, сходятся со светом в том отношении, что возмущения в любой точке поперечны к направлению распространения, и такие волны могут обладать всеми свойствами поляризованного света.
Единственной средой, в которой производились опыты для определения значения К (К - величина, пропорциональная квадрату скорости электромагнитной волны. - С. Ф.), был воздух... Согласно электромагнитным опытам Вебера и Кольрауша
υ = 310740000 метров в секунду
является количеством электростатических единиц в одной электромагнитной единице электричества, и это, согласно нашему результату, должно быть равно скорости света в воздухе или вакууме.
Скорость света в воздухе по опытам Физо равна:
V = 314858000,
а согласно более точным опытам Фуко
V = 298000000.
Скорость света в пространстве, окружающем Землю, выведенная из коэффициента аберрации и из величины радиуса земной орбиты, равна
V = 308 000 000.
...Следовательно, скорость света, определенная экспериментально, достаточно хорошо совпадает с величиной υ, выведенной из единственного ряда экспериментов, которыми мы до сих пор располагали. Значение υ было определено путем измерения электродвижущей силы, при помощи которой заряжается конденсатор известной емкости, разряжая конденсатор через гальванометр, чтобы измерить количество электричества в нем в электромагнитных единицах. Единственным применением света в этих опытах было использование его для того, чтобы видеть инструменты. Значение V, найденное Фуко, было получено путем определения угла, на который поворачивается вращающееся зеркало, пока отраженный им свет прошел туда и обратно вдоль измеренного пути. При этом не пользовались каким-либо образом электричеством и магнетизмом. Совпадение результатов, по-видимому, показывает, что свет и магнетизм являются проявлениями свойств одной и той же субстанции и что свет является электромагнитным возмущением, распространяющимся через поле в соответствии с законами электромагнетизма".
Из этого отрывка ясно, какое значение придавал Максвелл определению электродинамической постоянной. Будучи одним из величайших теоретиков в истории физической науки, Максвелл не чурался эксперимента. Уже после выхода в свет "Динамической теории электромагнитного поля" ученый решил опытным путем определить отношение электромагнитной и электростатической единиц заряда. Имелась и формальная причина, по которой Максвелл взялся за решение этой чисто экспериментальной задачи. Ученый был членом Комитета Британской Ассоциации содействия развитию науки, который в 1862 г. пришел к выводу о необходимости сравнения единиц двух систем для того, чтобы в целом упорядочить систему электрических единиц. Максвелл мог считать себя в определенной степени ответственным за выполнение этого решения. Обе причины, определившие интерес Максвелла к проблеме, нашли отражение в названии работы, в которой сообщалось о результатах опытов: "О методе прямого сравнения электростатической и электромагнитной сил, с замечанием об электромагнитной теории света". Эта статья была опубликована в "Философских записках" Лондонского Королевского общества за 1868 г.
Идея опыта состояла в сравнении силы электростатического притяжения, возникающей между двумя заряженными дисками (один из которых подвешен на конце коромысла крутильных весов, а другой находится внутри кожуха весов и может перемещаться лишь под действием микрометрического винта) с силой отталкивания, возникающей между катушками с током, помещенными вблизи дисков.
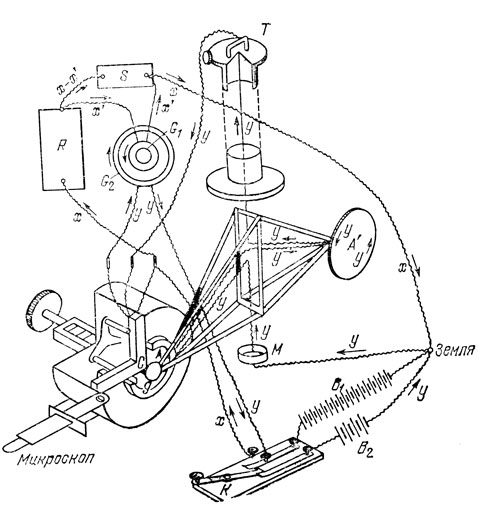
Рис. 16. Рисунок из работы Максвелла со схемой экспериментальной установки. В1 и В2 - источники постоянного тока, К - ключ, М - чаша со ртутью, А и А′ - катушки, подвешенные к противоположным концам коромысла крутильных весов, С - узел, содержащий подвижную пластину g и пластину, положение которой регулируется микрометрическим винтом, R - сопротивление, S - шунт, G1 и G2 - обмотки гальванометра, Т - регулировочный винт крутильного подвеса. Буквами у, х и х′ отмечены токи, протекавшие в различных частях установки
Схема установки, использованной Максвеллом, показана на рис. 16. В2 - батарея с небольшой э.д.с., созидающая ток y, протекающий через чашу со ртутью М, через две идентичные катушки А и А′, укрепленные на противоположных концах коромысла весов, через третью катушку (на рисунке неподвижный диск и закрепленная на нем катушка обозначены буквой С), катушку гальванометра G2 и ключ К. Вторая, высоковольтная батарея В1 состоявшая из 2600 элементов, создавала ток х, протекавший через ключ и сопротивление R = 1 МОм. После этого часть тока х′ протекала через вторую катушку гальванометра G1, а часть х - х′ - через регулируемый шунт S. Один из полюсов батареи В1 соединялся с неподвижной пластиной С, а подвижная пластина, на которой закреплялась катушка A, - с противоположным полюсом батареи.
Катушка А′ использовалась для компенсации воздействия на систему магнитного поля Земли. Перемещение пластины и катушки А осуществлялось посредством микрометрического винта; наблюдение за этим перемещением велось с помощью микроскопа. Поворот коромысла мог производиться винтом Т. Гальванометр и шунт были удалены от весов на расстояние около 3 метров.
Максвелл проводил измерения вместе с ассистентом Хоукином. Один из наблюдателей регулировал расстояние между притягивающимися пластинами до тех пор, пока притяжение между ними в точности не компенсировалось отталкиванием между кольцами. В положении равновесия нить, на которой висело коромысло, оказывалась незакрученной. Второй наблюдатель одновременно изменял шунт S таким образом, что стрелка гальванометра оказывалась в положении равновесия. В этих условиях действие сил со стороны токов, протекавших через катушки G1 и G2, компенсировалось. При достижении равновесия первый наблюдатель определял расстояние между пластинами.
Искомое отношение единиц зарядов определялось по следующей схеме. Благодаря использованию гальванометра с двумя катушками и проведению дополнительных измерений экспериментаторы могли с высокой точностью найти абсолютные значения токов, текущих через каждый из элементов электрической цепи.
Поскольку взаимодействие катушек гальванометра магнитное, величины токов оказываются определенными в магнитной системе единиц. Зная величины токов и сопротивлений, можно было найти напряжение, под которым находятся диски. Далее определялась величина заряда на дисках, которые образовывали конденсатор переменной емкости. Эта величина, естественно, выражалась в единицах магнитной системы.
Силу отталкивания между катушками с током, связанными с дисками, можно было рассчитать, поскольку геометрические размеры катушек и токи были известны. Эта сила по условию опыта равнялась силе электростатического притяжения между дисками. Но, зная эту силу и геометрические размеры образованного дисками конденсатора, легко рассчитать, какой заряд находится на его обкладках. Из этого расчета находится величина заряда, выраженная в электростатических единицах.
Таким образом, Максвеллу удалось, основываясь на независимых (!) измерениях, выразить величину одного и того же заряда, находившегося на пластинах, в единицах двух систем. Найти отношение единиц не составляло труда.
Первичная обработка результатов измерений дала величину υ, лежащую в пределах от 2,2⋅108 до 2,45⋅108 м/с. Однако большое расхождение с величиной скорости света навело Максвелла на мысль о том, что в опыте имеются неучтенные погрешности, И он, и Хоукин приложили немало усилий в поисках возможных источников ошибок. В итоге в публикации Максвелла было приведено значение υ = 2,88⋅108 м/с. Как видно из полученного результата, Максвеллу не удалось существенно увеличить точность измерений по сравнению с опытом Вебера и Кольрауша. Видимо, поэтому он продолжал размышлять над другими методами измерения υ, о чем свидетельствуют сохранившиеся записки ученого.
После измерений Вебера и Кольрауша, Максвелла и других ученых, занимавшихся определением электродинамической постоянной, после создания теории электромагнитного поля скорость света расширила свою "сферу влияния". В 1888 г. Генрих Герц (1857-1894) экспериментально доказал существование электромагнитных волн. После этого диапазон исследований, относящихся к скорости света, возрос - исследователей интересовало, одинакова ли скорость электромагнитных волн разных диапазонов. Но и оптические проблемы, касавшиеся скорости света, были еще далеко не исчерпаны. Именно к ним мы и обратимся.
|
ПОИСК:
|