
Глава V. Сколько у света скоростей?
1852 год. Для истории скорости света он весьма знаменателен, хотя никаких принципиально новых экспериментов тогда поставлено не было. Просто в этом году в небольшом городке Стрельно на территории современной Польши, входившей тогда в состав Германии, родился мальчик, имя которого впоследствии оказалось неразрывно связанным с проблемой измерения скорости света. Звали мальчика Альберт Абрахам Майкельсон.
Когда Альберту исполнилось два года, семья переехала в Соединенные Штаты Америки. В шестнадцать лет Майкельсон окончил среднюю школу в Сан-Франциско.
Материальные трудности большой семьи Майкельсонов сказались на выборе дальнейшего пути Альберта. Он поступил в Морскую академию Соединенных Штатов. Это высшее учебное заведение давало хорошее образование и, кроме, того, слушатели академии в течение всего срока обучения находились на казенном содержании и получали стипендию в размере 500 долларов в год.
Учился Майкельсон хорошо, но не блестяще. Особое сожаление руководителей академии вызывало то, что он совершенно не проявлял интереса к предметам, непосредственно связанным с будущей профессией моряка и отдавал предпочтение академическим дисциплинам: математике, оптике, акустике. В 1873 г. Майкельсон кончил курс и затем два года служил на кораблях военно-морского флота США. По окончании срока обязательной службы молодому человеку предложили место преподавателя физики и химии в Морской академии. Альберт с радостью принял предложение. Именно с этого времени начинается его научная деятельность.
Решение заняться научными исследованиями потребовало от Майкельсона определенной смелости. В академии, где он работал, не было никаких традиций в этой области. Эксперименты, задуманные Майкельсоном, приходилось ставить на собственные средства. Да и выбор тематики исследований был не так прост: легко было увлечься либо слишком сложной и непосильной темой, либо темой, лежавшей далеко от основных проблем физики того времени. Майкельсон сумел преодолеть эти трудности. Уже его первая научная работа была посвящена измерению скорости света. Эта задача вновь стала привлекать внимание физиков, работавших в разных уголках Земли.
Почему Майкельсон взялся за решение именно этой, весьма сложной задачи? Причин несколько. Во-первых, он с ранней юности интересовался оптикой. Во-вторых, незадолго до начала работы Майкельсона вышла в свет знаменитая книга Максвелла "Трактат об электричестве и магнетизме", в которой последовательно развивалась идея об электромагнитной природе света. Открытие Максвелла превратило скорость света из заурядной оптической константы в постоянную, играющую важнейшую роль в физике в целом. Не последним фактором, определившим выбор Майкельсона, были и лекции по оптике известного английского физика и популяризатора науки Джона Тиндаля (1820-1893), прочитанные им в Соединенных Штатах в 1876 г.
Прежде всего Майкельсон взялся за усовершенствование метода вращающегося зеркала Фуко. Довольно быстро ученому удалось превзойти точность измерений Фуко. О полученных результатах Майкельсон сообщил астроному С. Ньюкому (1835-1909), пользовавшемуся значительным авторитетом в правительственных кругах и проявлявшему интерес к проблеме измерения скорости света. Ньюком был настолько восхищен результатами, полученными молодым физиком, что добился в Национальной Академии наук выделения 5000 долларов на проведение новых опытов в этой области. Кроме того, он организовал переход Майкельсона из Морской Академии в редакцию Морского альманаха - учреждение, сотрудники которого занимались научной работой. Это позволяло двум ученым проводить опыты совместно.
Однако сотрудничество Майкельсона и Ньюкома длилось недолго. Двадцатисемилетний Майкельсон остро ощущал необходимость углубления своих знаний в области оптики. Для этого он выбрал, пожалуй, единственно возможный тогда путь - в 1880 г., получив отпуск, Майкельсон отправился в Европу. Там он работал у знаменитого немецкого ученого Г. Гельмгольца в Берлине, в Гейдельбергском университете, в Коллеж де Франс и Политехнической школе в Париже. В Европе он познакомился с известными физиками М. А. Корню, Э. Н. Маскаром, Рэлеем.
Знакомство Майкельсона с Уильямом Стреттом (лордом Рэлеем) имело для истории определения скорости света особое значение. Причиной, вызвавшей их совместное обсуждение научных проблем, был... ошибочный эксперимент.
Мы уже говорили о том, что английские ученые Юнг и Форбс пытались усовершенствовать метод Физо. Для этого они использовали схему, в которой свет отражался не от одного неподвижного зеркала, а от двух, находившихся на разных расстояниях от источника света и зубчатого колеса. Наблюдатель видел две близко расположенные светящиеся точки. Их яркость, вообще говоря, не одинакова вследствие различия расстояний до зеркал. Исследователи подбирали такую скорость вращения колеса, при которой обе точки казались одинаково яркими: они полагали, что метод сравнения позволит избежать ошибок, характерных для "абсолютных" измерений Физо, в которых требовалось определить момент наибольшего затемнения поля зрения.
Однако метод Юнга и Форбса породил новые трудности. Наблюдение удаленных точечных источников света почти всегда связано с явлением дифракции. При дифракции уже нельзя пользоваться представлениями геометрической оптики и законом прямолинейности распространения света: изображение, которое видел наблюдатель в опытах Юнга и Форбса, было не точкой, а системой колец.
Поскольку зеркала, участвовавшие в формировании дифракционных картин в зрительной трубе, находились на разных расстояниях от нее, то и сами дифракционные картины получались разными. Понятно, что правильно определить момент, когда сравниваются яркости двух разных изображений, гораздо труднее, чем при наблюдении одинаковых изображений. Детали дифракционной картины зависят от длины волны света, т. е. от его цвета. Это навело Юнга и Форбса на мысль исследовать скорость распространения света разных цветов. Проанализировав результаты опытов, они пришли к выводу, что синий свет распространяется в воздухе со скоростью, превышающей скорость красного света.
В описываемых опытах впервые с помощью прямых методов были получены данные о зависимости скорости света от его цвета, что, естественно, привлекло к ним внимание ученых. Однако далеко не все физики отнеслись к выводам Юнга и Форбса с полным доверием.
Сообщение об их опытах было опубликовано в журнале "Nature" ("Природа"). Этот еженедельник, выходящий в Лондоне, публиковал (и публикует в наши дни) краткую информацию о важнейших исследованиях в области естествознания. В некотором смысле это уникальный журнал. На его страницах не раз появлялись первые сообщения об открытиях физиков и химиков разных стран, впоследствии становившиеся основанием для признания приоритета того или иного ученого. Издатели журнала старались, чтобы публикуемые материалы были доступны всем, кто интересуется последними достижениями науки. Часто на страницах этого журнала появлялись письма ученых с обсуждением научных проблем - начинались научные дискуссии. Одна из таких дискуссий возникла в связи с сообщением об опытах Юнга и Форбса. Ее инициатором был Уильям Стретт.
Третий барон Рэлей, Уильям Стретт, принадлежит к блестящей плеяде английских ученых XIX в., внесших значительный вклад в развитие классической физики. Впрочем, Рэлей добился больших успехов не только в физике: вместе с химиком Уильямом Рамзаем (1852-1916) он открыл инертный газ аргон. Жизнь Рэлея лишена каких-либо ярких внешних событий. Он родился в 1842 г. в семье довольно богатого землевладельца. В отличие от многих известных английских естествоиспытателей, получивших дворянский титул в награду за свои научные достижения, Рэлей был дворянином по рождению. Из-за слабого здоровья Уильям не смог закончить Итон - привилегированную среднюю школу, куда по традиции отдавали своих детей английские аристократы. Тем не менее, он сумел подготовиться к поступлению в Тринити-колледж Кембриджского университета. В 1865 г. Рэлей успешно закончил университет, став первым на труднейшем экзамене.
Благодаря академическим успехам молодой физик после окончания университета стал членом (преподавателем) Тринити-колледжа. В это же время Рэлей начинает самостоятельные научные исследования. Его внимание привлекают вопросы акустики и физиологии слухового ощущения. Он интересуется также проблемами цветового зрения, теория которого была развита Т. Юнгом, Дж. К. Максвеллом и Г. Гельмгольцем. Однако основные усилия молодого ученого были направлены на развитие математического аппарата для решения широкого круга задач, относящихся к самым разнообразным областям физики.
В 1871 г. Рэлей женился и покинул Кембридж, поселившись в родовом поместье в Терлинге. Здесь Рэлей устроил домашнюю лабораторию и занялся экспериментами. В нем на редкость удачно сочетались способности теоретика и экспериментатора. Первые опыты Рэлея были посвящены фотографии, что усилило его интерес к проблемам оптики.
Эти эксперименты привели Рэлея к другой проблеме - рассеянию света; результаты, полученные Рэлеем в теории рассеяния, стали классическими.
В 1880 г. Рэлей прервал свое добровольное затворничество в Терлинге, приняв почетное предложение стать преемником Максвелла на посту директора Кавендишской лаборатории. Здесь ученый проработал пять лет. Деятельность Рэлея способствовала развитию Кавендишской лаборатории как учебного и исследовательского центра. Научные интересы Рэлея в этот период были сосредоточены на проблемах акустики и капиллярных явлениях.
После ухода из Кавендишской лаборатории Рэлей возобновил свои исследования в Терлинге - теперь его интересовали вопросы, относящиеся к электромагнетизму.
В 1900 г. вышла в свет его знаменитая работа, посвященная одной из центральных проблем физики конца XIX - начала XX вв. - излучению абсолютно черного тела.
В 1904 г. Рэлей был удостоен Нобелевской премии за исследование газов и открытие аргона. До самой смерти, последовавшей в 1919 г., он продолжал активную научную работу. Собрание сочинений Рэлея содержит 446 статей почти по всем разделам физики. При такой высокой продуктивности Рэлей практически не оставил пустых или ошибочных работ.
Особое внимание ученого с юности привлекали проблемы оптики; почти половина его работ посвящена этому разделу физики. Теоретическую оптику ученый рассматривал как часть теории волн и стремился развивать методы и представления, применимые к волнам любой природы. Именно с этим общим взглядом на физику волновых процессов и связано его письмо в "Nature". Оно начинается так:
"Опубликованный Юнгом и Форбсом результат, состоящий в том, что синий свет распространяется в вакууме со скоростью приблизительно на 1,8% большей, чем красный свет, поднимает интересный вопрос о том, что в действительности определяется такого рода наблюдениями".
Таким образом, Рэлей обращает внимание на необходимость тщательного анализа вопроса о том, что измеряется в эксперименте. Далее он ссылается на свою работу десятилетней давности, в которой показал, что часто при анализе волновых явлений приходится рассматривать не одну скорость, а две:
"Часто замечали, что когда группа волн распространяется в спокойной воде, то скорость группы меньше скорости отдельных волн, из которых она состоит: кажется, что волны проходят сквозь группу, затухая по мере их приближения к ее передней границе. Это явление было, я полагаю, впервые объяснено Стоксом, который рассматривал группу как результат наложения двух бесконечных рядов волн, имеющих равные амплитуды и почти равные длины волн и распространяющихся в одном и том же направлении"*.
* (В действительности впервые такая задача была рассмотрена в 1839 г. известным ирландским физиком У. Р. Гамильтоном (1805-1865). Однако ученый не опубликовал полностью результаты своих исследований, и в течение длительного времени его заслуги в этой области не были оценены по достоинству. Рэлей, по-видимому, не знал о работах Гамильтона, поэтому ссылался, как на своего предшественника, лишь на английского ученого Дж. Стокса (1819-1903).)
Попробуем и мы разобраться в том, что же такое скорость волн и какая скорость измеряется в реальных экспериментах.
Волна - это распространение колебаний в пространстве. Представление об этом физическом объекте формируется у нас сначала интуитивно. Многие любят наблюдать за бегом морских волн. Такой "бег" не приводит к значительному смещению больших масс воды: если наблюдать за лодкой в волнующемся море, то можно заметить, что она с течением времени лишь периодически поднимается и опускается, оставаясь на одном и том же месте. Этот пример хорошо иллюстрирует определение волны, данное выше. Если наблюдать за двумя лодками, расположенными на некотором расстоянии друг от друга вдоль линии, по которой "бегут" волны, то почти наверняка окажется, что лодки поднимаются и опускаются "не в такт". Это происходит потому, что гребень волны, который поднимает одну лодку, доходит до другой через некоторое время, и в тот момент, когда он поднимает вторую лодку, первая может оказаться вовсе не на гребне, а во впадине или в каком-нибудь промежуточном положении. Физики объясняют это тем, что волна распространяется с конечной скоростью. Переведем эти качественные рассуждения на язык математики.
Простейшее - гармоническое - колебание описывается формулой
A = A0cos(ωt + φ), (V.1)
где А - колеблющаяся величина (например, высота лодки относительно ее среднего положения), A0 - амплитуда колебания (т. е. величина, характеризующая максимальное отклонение лодки от среднего положения). Величина ω называется циклической частотой. Более привычная характеристика колебания - это период Т - промежуток времени между двумя последовательными моментами, соответствующими одинаковым состояниям системы (например, прохождению лодки через верхнюю точку ее траектории). Так как период косинуса равен 2π, то связь ω и T дается формулой ω = 2π/T. Величина ωt/+φ0 называется фазой колебания. Она определяет, какая часть колебания прошла с момента его начала. Поскольку при t = 0 фаза колебания равна φ0, то величину φ0 называют начальной фазой колебания. Отметим, что формула (V. 1) может описывать гармонические колебания разных величин: смещения тела, силы, напряженности электрического поля и т. д.
Когда говорят о волне, то подразумевают, что колебания охватывают целую область пространства (лодки качаются на некотором расстоянии друг от друга). Колебания в разных точках могут иметь разные фазы и амплитуды: этим-то и объясняются различия в движении лодок.
На рис. 17 показаны две "мгновенные фотографии" так называемой бегущей волны, характеризующие значения величины А в разных точках пространства, которые она принимает в моменты времени t1 и t2 (t2 > t1). Из рисунка видно, что гребень волны А0 за время Δt = t2 - t1 сдвинулся вправо на некоторое расстояние Δх. Если бы мы могли непрерывно следить за положением этого гребня, то увидели бы, что он перемещается, бежит: отсюда и название волны.
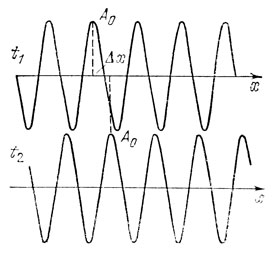
Рис. 17. 'Мгновенные фотографии' бегущей волны: гребень А0 за время Δt = t2 - t1 переместился на расстояние Δх
Такой процесс распространения колебаний можно описать с помощью формулы
А = А0cos(ωt - kx). (V.2)
Как видно, фаза колебаний зависит как от времени t, так и от координаты х. Величина k называется волновым числом. Она определяет наименьшее расстояние λ между двумя точками, колеблющимися в фазе (длину волны): k = 2π/λ.
Рассмотрение "фотографий" волны наводит на мысль о том, как определить скорость распространения бегущей волны. Из рис. 17 видно, что волна перемещается как единое целое, поэтому скорость движения гребня можно отождествить со скоростью всей волны. Пусть в момент времени t1 гребень находится в точке x1, а в момент времени t2 = t1 - Δt - в точке х2 = x1 + Δx. Физически это означает, что фазы колебаний в момент t1 в точке x1 и в момент t2 в точке х2 совпадают. Поэтому можно записать.
ωt1 - kx1 = ωt2 - kx2.
Скорость перемещения гребня υ = Δx/Δt и, следовательно, скорость волны
| υ = | ω | . (V. 3) |
| k |
Из сказанного ясно, что движение гребня можно рассматривать как "перемещение фазы", поэтому найденную нами скорость υ называют фазовой скоростью волны.
Однако проведенные рассуждения нельзя считать универсальными. Далеко не все волны в природе оказываются синусоидальными. В пространстве может распространяться последовательность импульсов ("гребней") любой формы. Предпочтение, которое физики отдают именно синусоидальным волнам, связано с тем, что любую волну можно представить в виде суммы некоторого числа (возможно, бесконечного) синусоидальных волн. Специальное математическое преобразование - преобразование Фурье - позволяет найти частоты и амплитуды волн-слагаемых. Таким образом, чтобы понять, как распространяются волны, достаточно рассмотреть движение нескольких синусоидальный составляющих. Посмотрим, возникают ли какие-либо особенности при исследовании движения не одной синусоидальной волны, а двух.
Допустим, что вдоль оси х в одном направлении распространяются две волны с одинаковыми амплитудами A0 с частотами ω1 и ω2 и волновыми числами k1 и k2 соответственно. Допустим, что частоты и волновые числа мало отличаются друг от друга. Результирующее колебание в точке пространства с координатой х можно представить в виде
A = A0[cos(ω1t - k1x) + cos(ω2t -k2x)] = 2A0cos(Δωt - Δkx)cos(ωt - kx), (V. 4)
где
| Δω = | ω2 -ω1 | , |
| 2 |
На рис. 18 показаны "мгновенные фотографии" этой группы волн. Из рисунка видно, что хотя огибающая группы практически не меняет своей формы, "наполнение" огибающей с течением времени изменяется. Согласно (V.4) колебание в любой точке пространства теперь определяется произведением двух периодических функций с существенно различающимися частотами Δω << ω. Как же определить скорость группы волн?
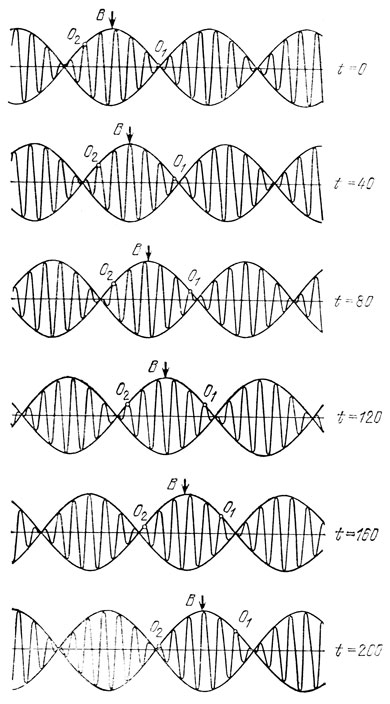
Рис. 18. 'Мгновенные фотографии' группы волн. Каждой фотографии соответствует некоторый условный момент времени t
Если мы хотим проследить за перемещением волнового фронта (т. е. поверхности постоянной фазы), то надо наблюдать за движением одного из гребней наполняющей (точки О1 и О2 на рис. 18); медленный рост гребня О1 и уменьшение "высоты" гребня О2 связаны с наличием в (V.4) медленно меняющегося члена cos (Δωt - Δkx). Если пренебречь изменением "высоты" гребня, то скорость его движения можно найти из уcловия постоянства фазы: ωt - kx = const. Рассуждения, которые необходимо провести, ничем не отличаются от тех, что были использованы при выводе формулы (V. 3), поэтому и ответ получается тот же: фазовая скорость группы волн, как и одной синусоидальной волны, равна υ = ω/k.
Однако к вопросу о скорости волны можно подойти иначе и рассмотреть движение максимума огибающей группы волн (на рис. 18 он указан стрелками В). Какова скорость перемещения этого максимума?
Поскольку Δω << ω, множитель cos (ωt - kx) в формуле (V. 4) определяет расстояние между максимумами "наполнения", а множитель cos (Δωt - Δkx) - расстояние между максимумами огибающей. Этот последний и характеризует движение огибающей. Условие ее максимума, очевидно, можно записать в виде
Δωt - Δkx = 2πn (n = 0, 1, 2, ...). (V. 5)
С течением времени координата х максимума с данным n будет меняться - он будет двигаться. Для момента времени t + Δt условие (V. 5) запишется в виде
Δω(t + Δt) - Δk(x + Δx) = 2πn. (V.6)
Из (V. 5) и (V. 6) нетрудно получить соотношение
ΔωΔt = ΔkΔx.
Тогда скорость движения максимума огибающей Δk → 0, получаем
| u = | dω | . |
| dk |
Величину u называют групповой скоростью волн. Если внимательно присмотреться к рис. 18, то можно увидеть, что перемещения максимума, указанного стрелкой, и максимума, отмеченного точкой, происходят по-разному. Иначе говоря, для случая, изображенного на этом рисунке, υ ≠ u.
Зачем нужно введение понятия групповой скорости? Во многих случаях распространение волн связано с переносом энергии. Форма огибающей группы волн дает общее представление о распределении энергии волн в пространстве, а скорость движения максимума - групповая скорость - характеризует быстроту переноса энергии. Поскольку любая передача информации связана с переносом энергии, определение групповой скорости волн оказывается важной физической задачей.
Всегда ли групповая скорость отличается от фазовой? К каким следствиям приводит это различие? Для ответа на эти вопросы нужно знать, как связаны между собой υ и u. Читатель, умеющий дифференцировать, может без труда убедиться, что величины фазовой и групповой скоростей связаны соотношением
| u = υ - λ | dv | . (V. 8) |
| dλ |
Эта формула была впервые выведена Рэлеем в 1871 г. и теперь носит его имя. Сам Рэлей использовал ее прежде всего при рассмотрении волн, возникающих на поверхности воды. Различают два основных типа таких волн: гравитационные и капиллярные. Образование гравитационных волн обусловлено действием силы тяжести; они возникают в тех случаях, когда силам другой природы (негравитационными) можно пренебречь; длины гравитационных волн велики. В образовании капиллярных волн, которые характеризуются значительно меньшими длинами волн, решающую роль играют силы поверхностного натяжения. Во времена Рэлея зависимости фазовых скоростей этих типов волн от λ были уже известны, поэтому можно было найти их групповые скорости. Заметим, что поскольку для гравитационных волн υ ~ λ-1/2, то для них υ > u, в то время как для капиллярных волн (υ ~ λ-1/2) υ < u.
Теория Рэлея применима, в принципе, к волнам любой природы. Однако ее непосредственное распространение на световые волны сталкивалось со значительными трудностями.
Напомним, что согласно теории Гюйгенса величина скорости света в веществе и значение коэффициента преломления n связаны между собой. Во второй половине XVII в. Ньютон тщательно исследовал явление дисперсии света, доказав, что свет разных цветов может преломляться по-разному и, следовательно, каждому цвету поставить в соответствие свой коэффициент преломления. Таким образом, уже в конце XVII в. стало ясно, что скорость света в веществе зависит от его цвета. В начале XIX в., после победы волновой теории, идея о зависимости скорости света в прозрачных веществах от λ стала общепризнанной. О какой же скорости - групповой или фазовой - шла речь?
При выводе закона преломления Гюйгенса рассматривал положение волновых фронтов (т. е. поверхностей равных фаз) падающей и преломляющей волн. Из всего сказанного выше ясно, что если рассматривается движение волнового фронта, то речь может идти только о фазовой скорости. Поэтому можно утверждать, что физики издавна имели сведения о зависимости фазовой скорости света от длины волны.
Рэлей поставил принципиальный вопрос: какая скорость определяется в "прямых" опытах* по измерению скорости света? Вопрос касался и астрономических, и "земных" методов. Ученому удалось показать, что во всех прямых экспериментах измерялась групповая скорость света. Качественно этот вывод Рэлей поясняет следующим образом:
* ("Прямыми" называются опыты, в которых для определения скорости света непосредственно измеряются длина пути и время его прохождения.)
"Если бы мы наблюдали, что гребень обычной волны в воде движется со скоростью одного фута в секунду, то мы, не колеблясь, утверждали бы, что это была скорость волны, и я предполагаю, что на обычном языке сторонников волновой теории скорость света точно так же означает скорость, с которой распространяется отдельная волна. Однако очевидно, что в случае света или даже звука мы не имеем средств для отождествления отдельной волны, чтобы определить скорость ее распространения. То, что мы делаем в большинстве случаев в действительности, сводится к тому, что мы накладываем какую-нибудь особенность, либо в отношении интенсивности, либо - длины волны, либо - поляризации на часть в остальном непрерывного ряда волн и определяем скорость, с Которой эта особенность распространяется. Так, в опытах Физо и Корню, а также в опытах Юнга и Форбса, свет делается прерывистым при помощи зубчатого колеса, в результате чего мы имеем скорость группы волн, а не непременно скорость отдельных волн (фазовую скорость - С. Ф.)".
Остается добавить, что метод Фуко, в котором используется вращающееся зеркало, также позволяет измерить лишь групповую скорость света.
Однако теория - теорией, а подтвердить ее опытным путем не удавалось. Основным препятствием для этого были экспериментальные трудности, связанные с измерением скорости света в веществе. Они весьма значительны сами по себе, а ведь для подтверждения теории Рэлея требовалось измерить скорость света с разными длинами волн! Заметим, что даже в веществах с сильной дисперсией фазовые скорости световых волн с разными К различаются всего лишь на несколько процентов. Значит, погрешность измерения скорости света не должна превосходить 1%. В связи с этим можно вспомнить неудачные попытки Корню увеличить точность измерений с.
Правда, в одном отношении теория Рэлея с появлением результатов Юнга и Форбса доказала свою плодотворность - несоответствие результатов, полученных английскими учеными, предсказаниям этой теории указывало на несовершенство экспериментальной методики. Однако вряд ли создатель теории был полностью удовлетворен этой "критической" ролью своего детища.
Рэлей мечтал о повышении точности экспериментов по определению скорости света. К этому же стремился и молодой Майкельсон. Аналогичную задачу ставили перед собой Юнг и Форбс. Все они были искренне заинтересованы в установлении истины, поэтому возникшая дискуссия оказалась весьма острой. Вслед за письмом Рэлея, в котором обсуждались экспериментальные данные Юнга и Форбса, на страницах "Nature" появилось письмо Майкельсона, в котором он выразил несогласие с выводами английских физиков. Письмо заинтересовало Рэлея - так началась его многолетняя переписка с Майкельсоном. Майкельсона чрезвычайно ободрил интерес Рэлея к его работе по измерению скорости света. Он поставил проверочные эксперименты по определению скорости света в воздухе, которые опровергли выводы Юнга и Форбса. Затем Майкельсон приступил к измерениям скорости света в воде и сероуглероде. И здесь он столкнулся с неожиданным результатом. Отношение скорости света в воздухе к скорости света в воде, определенное из измерений, было очень близко к значению показателя преломления воды. Однако с сероуглеродом дело обстояло иначе: показатель преломления для сероуглерода в использовавшемся диапазоне длин волн не превышал 1,66 (см. таблицу). В то же время измерения скорости света дали результат u = c/1,77. Расхождение данных расчета и опыта значительно превосходили, по оценкам Майкельсона, возможные погрешности измерений. Поэтому, несмотря на то, что он сам не мог объяснить полученные результаты, Майкельсон решил опубликовать данные опытов.

Детальное объяснение полученных Майкельсоном результатов практически одновременно дали Рэлей и американский физик Дж. У. Гиббс (1839-1903). Оно основывалось на теории Рэлея о связи групповой фазовой скоростей. Попробуем проанализировать данные Майкельсона с этой точки зрения.
Поскольку Майкельсон в своей работе пользовался усовершенствованным методом Фуко, его измерения давали величину групповой скорости света. Как уже говорилось, показатель преломления характеризует фазовую скорость. На рис. 19 показан график зависимости отношения υ/c (υ - фазовая скорость света в сероуглероде, с - скорость света в воздухе) от длины волны света λ; график построен по данным таблицы. Видно, что точки лежат близко к прерывистой прямой, поэтому легко определить значение производной
| d(υ / c) | ||
| dλ |
(напомним, что значение производной функции в данной точке численно равно тангенсу угла наклона касательной к кривой, описывающей эту функцию). Из рис. 19 следует, что
| d(υ / c) | = 0,088 мкм-1. | |
| dλ |
Отсюда по формуле Рэлея (V. 8) для средней длины волны λ = 0,55 мкм можно найти величину групповой скорости u = с/1,73, что близко к значению u, полученному Майкельсоном (u = с/1,77).
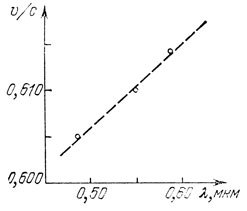
Рис. 19. Зависимость относительной фазовой скорости света υ/с в сероуглероде от длины волны света λ
Таким образом, неожиданный результат опытов Майкельсона стал первым подтверждением теории Рэлея применительно к свету. Теперь можно было смело утверждать, что свет характеризуется не одной скоростью, а двумя - фазовой и групповой.
В опытах Майкельсона групповая скорость света оказалась меньше фазовой. Всегда ли выполняется это соотношение? Из формулы (V. 8) следует, что если производная
| dυ | ||
| dλ |
положительна, то υ > u, если она отрицательна, υ < u. В оптике первому случаю отвечает обычная дисперсия, когда показатель преломления n растет с уменьшением длины волны - именно в этой области проводил опыты Майкельсон. Однако известно и другое оптическое явление - аномальная дисперсия, когда в некотором диапазоне длин волн показатель преломления уменьшается с уменьшением λ. Соответствующая зависимость n(λ) показана на рис. 20, где штриховкой отмечена область аномальной дисперсии. Заметим, что аномальная дисперсия наблюдается на участке спектра, где велико поглощение света веществом; она обусловлена особенностями поведения молекул вещества в случаях, когда частота падающего света близка к собственной частоте колебаний молекул. В области спектра, где наблюдается аномальная дисперсия, очевидно, u < v*.
* (При этом, конечно, остается справедливым вывод теории относительности о том, что групповая скорость (скорость передачи энергии) не может быть больше скорости света в вакууме (см, гл. VI).)
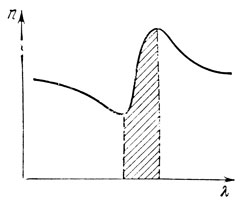
Рис. 20. Зависимость коэффициента преломления среды n от длины волны λ в области аномальной дисперсии (заштрихована)
Механизм распространения электромагнитных волн в веществе можно представить себе так. Падающая электромагнитная волна возбуждает вынужденные колебания электронов, входящих в состав атомов и молекул. Всякий колеблющийся заряд, согласно законам электродинамики, излучает электромагнитные волны, характеризующиеся частотой, с которой колеблется заряд. Таким образом, в веществе происходит как бы "переизлучение" электромагнитных волн.
Вынужденные колебания электронов всегда происходят с частотой падающей волны. Однако их амплитуда тем больше, чем ближе эта частота к частоте собственных колебаний электронов в атомах и молекулах (резонанс). Поэтому особенности процесса переизлучения определяются соотношением между собственными частотами колебаний электронов вещества и частотой падающей волны. В результате и скорость распространения электромагнитных волн в веществе неизбежно зависит от их частоты. Дисперсия волн не наблюдается лишь в вакууме, где вещество отсутствует - только в этом случае в точности выполняется равен u = υ.
Введение понятий фазовой и групповой скоростей волн, как мы видели, необходимо. Однако даже с "по-мощью" двух скоростей не всегда удается полностью описать физическую ситуацию. Оказывается, что в случае сильной дисперсии (т. е. когда производная
| dυ | ||
| dλ |
велика) и (или) при широком спектре сигнала (т. е. когда сигнал можно представить в виде суммы некоторого числа синусоидальных волн с существенно различными λ) использование понятия групповой скорости оказывается малоэффективным. Причину этого можно легко понять, рассмотрев рис. 21, на котором изображены "фотографии" волны, распространяющейся вдоль оси х. В момент t = 0 волна представляет собой периодическую последовательность импульсов почти прямоугольной формы. В действительности, эта волна - сумма 15 синусоидальных волн с частотами ω, 2ω, ..., 15ω. Волна распространяется в среде с сильной дисперсией, поэтому фазовые скорости составляющих существенно различаются. Вследствие этого через достаточно большой промежуток времени форма импульсов, из которых складывается волна, меняется до неузнаваемости. В данном случае уже не удается выбрать точку, за движением которой можно было бы следить для нахождения скорости волны. В такой ситуации для описания физических процессов пользуются другими представлениями*. Тем не менее и в этом случае скорость переноса энергии никогда не превышает скорость света в вакууме.
* (Отметим, что выше описана упрощенная картина распространения электромагнитных волн в веществе, характерная для установившегося режима движения волны. При более строгом рассмотрении необходимо учитывать особенности движения переднего фронта сигнала (так называемого "первого предвестника"), на которых мы не можем здесь останавливаться.)
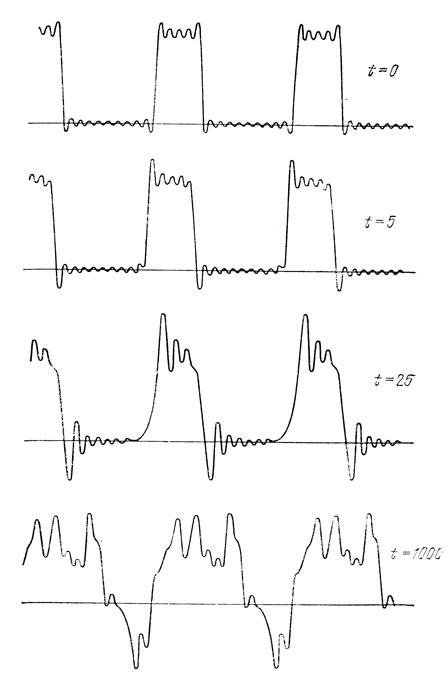
Рис. 21. Изменение формы волны с течением времени при наличии сильной дисперсии. Цифры у графиков соответствуют условным 'моментам' времени t
Решающим моментом в признании ошибочности выводов Юнга и Форбса стала конференция Британской ассоциации содействия развитию науки, состоявшаяся в 1884 г. в Монреале. Рэлей, как президент ассоциации, привлек внимание участников конференции к вопросу о скорости света в воздухе. Необходимо отметить, что хотя к этому времени результаты опытов Майкельсона по измерению скорости света в сероуглероде уже были опубликованы, мнение ученых в оценке работы Юнга и Форбса расходились. Так, известный ирландский физик-теоретик Дж. Фитцджеральд (1851-1901) выступил с докладом, в котором утверждал, что голубой свет распространяется быстрее красного не только в воздухе, но и в вакууме. Дискуссия, развернувшаяся на конференции, закончилась победой сторонников теории Рэлея. Немалую роль в этой победе сыграл доклад "О скорости света в сероуглероде", прочитанный Майкельсоном.
Точность, с которой Майкельсон проводил свои измерения, привлекла внимание патриарха английской физики Вильяма Томсона (лорда Кельвина) (1824-1907) к его работам. Кельвин и Рэлей посоветовали Майкельсону заново поставить опыт, который тот пытался осуществить еще во время своего пребывания в Европе в 1881 г. Этот опыт касался вопроса о скорости распространения света в движущихся средах. Европейские физики, пользовавшиеся огромным авторитетом в науке, поверили, что молодому американцу под силу решить задачу, волновавшую ученых уже несколько десятилетий. Майкельсон внял этим советам и смело принялся за работу.
|
ПОИСК:
|