
Глава VI. Скорость света и движение тел
Как правило, развитие физической теории идет по пути усложнения рассматриваемых ею задач. Это утверждение относится и к оптике. Для проблемы определения скорости света естественным усложнением был переход к исследованию распространения света в движущихся телах.
Зарождение этой проблемы относится к концу XVII - началу XVIII в. Важнейшим оптическим эффектом, для анализа которого требовалось решение вопроса о влиянии движения тел на распространение света, было явление аберрации света. Действительно, как мы помним, аберрация света обусловлена относительным движением звезды, являющейся источником света, и Земли, на которой производятся наблюдения. Поэтому для объяснения эффекта необходимо установить связь между движением света и движением Земли относительно "неподвижных" звезд. Брадлей, открывший явление и давший ему первое теоретическое объяснение, при вычислении угла аберрации пользовался правилом сложения скоростей, которое является следствием принципа относительности Галилея.
Для сторонников корпускулярной теории света такая точка зрения казалась вполне естественной. Во второй половине XVIII в. была даже высказана идея проверочного эксперимента: предлагалось заполнить астрономическую трубу водой и определить в этих условиях угол аберрации. Поскольку скорость света в воде, согласно корпускулярной теории света, больше чем в воздухе, угол аберрации должен был уменьшиться. Этот опыт был проделан, правда, лишь сто лет спустя. Забегая вперед, скажем, что его результат оказался отрицательным - изменение угла аберрации обнаружить не удалось.
Теория аберрации света не привлекала особого внимания оптиков вплоть до конца XVIII в. Положение резко изменилось вследствие развития волновой теории. Юнг и Френель рассматривали свет как волновой процесс, происходящий в специальной среде - эфире. Свойства этого - светоносного - эфира были довольно странными: он должен был обладать ничтожной плотностью и в то же время характеризоваться очень высокой упругостью, т. е. быть практически твердым. Однако для нас сейчас интересны не эти парадоксальные свойства эфира, а вопрос о его увлечении движущимися телами.
В зависимости от того, был ли эфир неподвижным или увлекался телами при их движении, многие оптические эффекты должны были выглядеть по-разному.
Первая попытка рассмотрения аберрации на основе волновой теории принадлежит Юнгу. Он основывался на гипотезе неподвижного эфира и получил результат, совпадающий с выводами корпускулярной теории.
Несколько лет спустя Араго попытался решить вопрос об увлечении эфира экспериментально. Для этого он исследовал преломление света в призме. Источником света были звезды. Согласно рабочей гипотезе Араго при приближении Земли к звезде скорость света должна была складываться со скоростью Земли, а при удалении Земли от звезды результирующая скорость должна была равняться разности этих скоростей. Волновая теория, как уже отмечалось, связывает величину скорости света в веществе (в данном случае - в веществе призмы) с его коэффициентом преломления. Поэтому при движении Земли (и призмы) к звездам коэффициент преломления вещества призмы должен был отличаться от коэффициента преломления, характерного для случая удаления Земли от звезды. Это различие должно было проявляться в изменении угла отклонения светового луча при прохождении через призму. По оценкам Араго в случае справедливости этого предположения видимая разность в отклонении лучей, прошедших через призму, могла составлять 2′; эта величина вполне доступна измерению. Однако, несмотря на все попытки, ученому не удалось обнаружить никакого различия в преломлении при изменении направления движения Земли относительно звезды. Сам Араго не мог найти объяснения этому факту, поэтому он обратился к своему другу и коллеге Френелю с просьбой указать причину отрицательного результата экспериментов. Френель ответил Араго письмом, которое было опубликовано в 1818 г. Оно по справедливости считается началом развития целой области оптики - оптики движущихся тел.
История показала, что с исследования Френеля (а к его письму следует относиться именно как к серьезной научной работе) началась разработка не частного вопроса, а фундаментальной проблемы, решение которой потребовало пересмотра основных физических представлений.
Вот что писал Френель в этом письме:
"Вы просили меня исследовать, не могут ли результаты этих наблюдений лучше быть согласованы с системой, согласно которой свет представляет собой колебания всепроникающей жидкости (эфира. - С. Ф.)... Если предположить, что наш земной шар сообщает свое движение эфиру, которым он окружен, можно было бы легко понять, почему та же самая призма всегда преломляет свет одним и тем же образом, независимо от того, с какой стороны этот свет подходит. Однако с точки зрения этой гипотезы оказывается, по-видимому, невозможным объяснить явление аберрации звезд: я, по крайней мере, до сих пор мог четко понять это явление, только предполагая, что эфир свободно проходит через, земной шар и что скорость, сообщаемая этой тонкой жидкости, представляет собой только небольшую часть скорости Земли и не превышает, например, одной сотой доли этой скорости".
Френель не только высказал качественные соображения относительно взаимодействия эфира и движущегося тела, но и предложил расчет так называемого "коэффициента увлечения", показывающего, какая часть скорости тела сообщается эфиру. Рассуждения Френеля сводятся к следующему.
Свет распространяется в упругом эфире. Плотность эфира в веществе ρ больше, чем плотность ρ′ вне его (при одинаковой упругости). Скорость распространения световых возмущений обратно пропорциональна квадратному корню из плотности эфира, поэтому
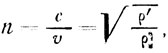
где υ - скорость света в веществе, с - вне его.
При движении тела плотность эфира внутри него остается неизменной. Согласно представлениям Френеля это происходит потому, что вместе с телом движется лишь часть содержащегося в нем эфира, которая обеспечивает превышение плотности эфира в веществе над его плотностью в окружающем пространстве.
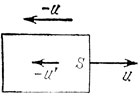
Рис. 22. К расчету френелевского коэффициента увлечения эфира
Пусть тело движется по отношению к эфиру со скоростью u, т. е. эфир вне тела обтекает его со скоростью - u. Однако внутри тела скорость эфира по отношению к этому телу иная. Действительно, при движении тела должно выполняться условие неразрывности эфира на поверхности тела S (рис. 22). Это условие означает, что количество эфира, втекающего в тело в единицу времени через единицу поверхности, должно равняться количеству эфира, оттекающего от единицы этой поверхности внутрь тела:
uρ = u′ ρ′.
Так как ρ ≠ ρ ′, то u ≠ u′. Используя выражение для коэффициента преломления n, нетрудно найти скорость эфира, движущегося внутри тела, по отношению к внешнему неподвижному наблюдателю:
| u″ = u′ - u = (1 - | 1 | )u. |
| n2 |
Из формулы (VI. 1) следует, что для внешнего наблюдателя процесс распространения света в движущемся теле выглядит так, как если бы эфир двигался не со скоростью тела u, а со скоростью u′. Поэтому в зависимости от направления движения тела результирующая скорость света в теле относительно неподвижного наблюдателя равна
| υ′ = | c | ± (1 - | 1 | )u, |
| n | n2 |
причем знак минус соответствует движению света навстречу телу, знак плюс - движению света и тела в одном направлении. Из приведенного вывода ясно, почему коэффициент μ = 1 - 1/n2 получил название коэффициента частичного увлечения.
Работа Френеля обладала одним важным достоинством. Она не только объясняла отрицательные результаты опытов Араго, но и приводила к выводу, допуcкавшему, в принципе, экспериментальную проверку - скорость света в движущемся теле отлична от скорости света в неподвижном теле.
Несмотря на идейную простоту опыта, который должен был стать проверкой для всей теории Френеля, долгие годы никто не решался взяться за его постановку.
Между тем физики-теоретики пытались рассмотреть задачу Френеля с других позиций. Наибольшую известность получили работы, выполненные в этой области Дж. Стоксом. Он иным методом получил то же, что и Френель, выражение для коэффициента увлечения.
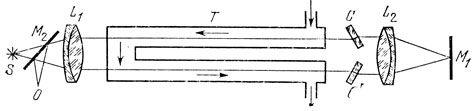
Рис. 23. Схема опыта Физо по измерению скорости света в движущейся воде. S - источник света, М2 - полупрозрачная пластинка, L1 и L2 - линзы, С и С′ - регулировочные пластины, М - плоское зеркало, Т - труба с водой, О - точка, в окрестности которой формируется интерференционная картина
Впервые исследовать распространение света в движущейся жидкости отважился И. Физо. Подчеркнем, что ученый не ставил своей целью определение абсолютной величины скорости света в воде (неподвижной или движущейся). Его интересовала зависимость скорости света от скорости движения воды; иными словами, он хотел экспериментально найти величину коэффициента увлечения и сравнить полученный результат с предсказанием теории Френеля.
В рассказе о ранних оптических исследованиях Физо уже отмечалось, что он был непревзойденным мастером интерференционных экспериментов. Эта черта его таланта проявилась и в постановке опыта с движущейся водой. Схема эксперимента показана на рис. 23.
Свет от источника S шел через полупрозрачную пластину М2 к линзе L1 до линзы свет проходил через две щели так, что после L1 формировались два узких параллельных световых пучка, каждый из которых шел через одно из колен (длина l = 1,487 м) П-образной стеклянной трубы Т, наполненной водой. После трубы свет попадал на регулировочные плоскопараллельные пластины С и С′ и собирающую линзу L2, в фокальной плоскости которой находилось плоское зеркало М1. Установка регулировалась таким образом, чтобы луч, прошедший сначала нижнее колено трубы, возвращался к линзе L1 и пластинке М2 через верхнее колено, в точности повторяя путь луча, проходящего от L1 к зеркалу M1 через верхнее колено. Луч, проходивший сначала верхнее колено трубы, после отражения от М1 двигался через нижнее колено. Таким образом, пути лучей через трубу оказывались в точности равными друг другу. Выполнение этого условия было необходимо для устранения влияния побочных факторов на распространение света (неравномерный нагрев различных частей установки, приводящий к изменению их размеров и колебаниям плотности жидкости и т. д.). При использованной схеме эти факторы одинаково влияли на оба луча и, следовательно, интерференционная картина, формировавшаяся после отражения лучей от пластины М2 в окрестности точки О, не менялась.
Для наблюдения интерференции в точке О Физо по существу использовал двухщелевую схему, аналогичную схеме Юнга: волна от источника S разбивается на две части, каждая из которых проходит определенный оптический путь. Затем в некоторой области пространства происходит наложение этих частей - возникает интерференция. Наблюдатель через зрительную трубу видит в окрестности точки О чередование темных и светлых полос; с помощью окулярной шкалы можно измерить ширину одной полосы. Ширина интерференционных полос зависела от расстояния между изображениями щелей, формировавшимися оптической системой, которые могут рассматриваться как источники, создающие интерференционную картину. Чем ближе располагаются такие источники, тем больше ширина интерференционных полос. Поскольку внутренний диаметр стеклянной трубы составлял 5,3 мм, расстояние между параллельными световыми пучками, проходящими через разные колена, не могло быть сделано очень малым. Но при большом расстоянии между источниками наблюдать интерференцию крайне трудно. Поэтому Физо пришлось использовать дополнительную стеклянную пластину (на схеме рис. 23 она отсутствует), помещавшуюся на пути света от одной из щелей. Пластина располагалась наклонно; вследствие преломления пучок света смещался параллельно самому себе. В итоге условия интерференции двух световых пучков менялись таким образом, как если бы сближались сами щели.
В своих наблюдениях Физо использовал солнечный свет. Постоянство скорости движения жидкости обеспечивалось с помощью пневматического устройства: вода под действием сжатого воздуха попеременно перекачивалась из одного резервуара в другой. Максимальная скорость течения достигала 7 м/с.
Измерения проводились следующим образом. Сначала фиксировалось положение некоторой интерференционной полосы при неподвижной воде. Затем вода приводилась в движение. По замыслу Физо, если движение среды действительно оказывает влияние на распространение света, то условия интерференции света, прошедшего через движущуюся воду, должны измениться. Действительно, два пучка света теперь оказываются в неравных условиях: один из них два раза проходит через трубу навстречу движущейся воде, а второй - в одном с ней направлении. Вследствие этого между соответствующими лучами должна возникнуть дополнительная разность хода, что приводит к смещению интерференционной картины. Задача наблюдателя - с возможно большей точностью измерить это смещение. Физо при проведении опыта делал два измерения - он пропускал жидкость через трубу сначала в одном направлении, фиксируя положение определенной полосы, а затем менял направление движения воды. При этом, естественно, менялось и направление смещения выбранной Интерференционной полосы по отношению к ее положению при неподвижной воде. Равенство смещений в одну и другую сторону при изменении направления движения воды (при постоянном абсолютном значении ее скорости) свидетельствовало о надежности полученных результатов.
В соответствии с предположениями Физо удалось наблюдать смещение интерференционных полос и тем самым доказать, что движение среды влияет на распространение света. Этот результат опровергал теорию, в которой эфир предполагался неподвижным. В то же время выбор между теорией полного увлечения эфира и теорией частичного увлечения Френеля мог быть сделан только на основе анализа величины смещения.
Согласно теории полного увлечения скорость света в движущейся воде относительно неподвижного наблюдателя равна υ′ = с/n ± u (с - скорость света в вакууме, т - показатель преломления, u - скорость среды*. Поэтому свет, идущий навстречу течению воды, пройдет расстояние 2l за время t1 = 2l/( c/n - u), а свет, идущий по течению, - за время t2 = 2/l (c / n + u). Поэтому
| Δt = t1 - t2 = | 4lu | . |
| (с / n)2 - u2 |
* (О правиле выбора знаков см. с. 116. )
Зная разность времен Δt, можно найти разность хода, возникающую между двумя лучами: Δ = cΔt. Удобнее рассматривать величину Δ/λ (λ - длина волны света), показывающую сколько длин волн составляет разность хода Δ. Поскольку с/n >> u, можно записать Физо проводил опыты со светом с длиной волны λ = 5260 °А* (такой свет, по мнению Физо, в наименьшей степени ослабляется при прохождении через воду). Оценка величины Δ/λ на основе теории полного увлечения эфира дает (u = 7 м/с, n = 1,33)
| Δ | = 0,46. | |
| λ |
* (1 °А, ангстрём - по фамилии шведского физика А. Ангстрёма, равен 10-10 м. )
Из данных Физо, полученных после проведения 19 серий измерений, следовало, что
| Δ | = 0,23. | |
| λ |
Расхождение между данными опыта и предсказанием теории полного увлечения явно превосходило возможные погрешности наблюдений.
Теория частичного увлечения Френеля приводит к иным выражениям для t1 и t2:
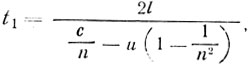
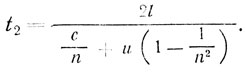
Следовательно,
| Δ | ≈ | 4l | u | (n2 - 1). | ||
| λ | λ | c |
Численная оценка этой величины дает Δ/λ = 0,2. Этот результат расчета гораздо лучше соответствует экспериментальным данным, однако расхождение между расчетом и данными опыта все же достаточно велико - 15%. С присущей ему тщательностью Физо проанализировал возможные причины этого расхождения. Он пришел к выводу, что основная погрешность измерений связана с определением скорости течения жидкости. Эта скорость определялась по количеству жидкости, вытекавшей из трубы в единицу времени. Физо справедливо отметил, что такая методика позволяет найти лишь среднюю скорость жидкости. В действительности же из-за вязкости жидкости и трения о стенки скорость течения вблизи оси трубы больше, чем у стенок. Оптическая схема опыта такова, что свет распространяется вдоль оси трубы, и сечение светового пучка составляет лишь 1/5 внутреннего сечения трубы. Поэтому свет проходит через ту часть жидкости, которая движется со скоростью, большей средней. Учет этого обстоятельства, как легко видеть (в оценке по теории Френеля следует взять большую величину для и), улучшает соответствие между расчетом и данными опыта. Кроме того, Физо отмечал, что ошибки в определении величины Δ могли быть связаны с тем, что наблюдатель вынужден был проводить измерения очень быстро - объем резервуаров с водой не позволял длительное время обеспечивать стационарное течение воды. Преодоление этой трудности, по словам Физо, требовало бы внесения слишком больших изменений в экспериментальную установку, поэтому ученый не использовал эту возможность повышения точности опыта.
Физо проводил эксперименты не только с движущейся водой. Он попытался также обнаружить влияние движения воздуха на скорость распространения света. Однако опыт дал отрицательный результат, который Физо также рассматривал как подтверждение теории Френеля. Коэффициент преломления воздуха очень близок к единице, n = 1,0003. Нетрудно оценить возможное смещение полос интерференции при тех же параметрах установки, что и в опытах с водой: Δλ = 1,5×10-4. Из оценки следует, что если бы Физо удалось обнаружить смещение полос в экспериментах с движущимся воздухом, то это было бы свидетельством не в пользу теории Френеля.
Глубокий анализ условий проведения опыта и его результатов позволил Физо прийти к такому выводу:
"Успех этого эксперимента, мне кажется, должен повлечь за собой принятие гипотезы Френеля, либо по крайней мере закона, который он нашел для изменения скорости света вследствие влияния движения тел. Действительно, хотя этот закон оказался правильным, имеется лишь одно убедительное свидетельство в пользу гипотезы, которое подтверждает лишь следствие из нее. Может быть, концепция Френеля покажется столь необычной, и, по некоторым отзывам, приемлемой лишь с большим трудом, вследствие чего потребуются новые доказательства и углубленный анализ со стороны математиков, прежде чем она будет рассматриваться как отражение реального положения вещей".
Однако опыты Физо не решили окончательно проблему связи между эфиром и движением тел. Их, скорее, можно рассматривать как начало пути, приведшего к разрешению этой проблемы. Из высказывания самого Физо следует, что хотя формула Френеля и получила подтверждение, теоретические предпосылки, на которых она основана, представлялись довольно искусственными. Не очень ясно, например, как объяснить с помощью теории Френеля распространение света в движущейся среде при наличии дисперсии. Каждой длине волны в среде с дисперсией соответствует свой показатель преломления. О каком увлечении избытка плотности эфира в этом случае идет речь?
Опыт Физо рассматривался физиками как один из основных экспериментов оптики движущихся тел. Неудивительно поэтому, что этот опыт впоследствии не раз повторялся. Однако повторялась лишь идея; в схему установки и в методику измерений вносились все новые и новые усовершенствования.
Первым на постановку опыта по модифицированной схеме Физо в 1886 г. отважился Альберт Майкельсон в сотрудничестве с Э. Морли. Американские физики уточнили данные Физо. Еще более точные измерения провели голландский физик П. Зееман (1865-1943) и его сотрудники в 1914 г. Эта группа экспериментаторов для регистрации полос использовала фотографию. Голландским физикам удалось выполнить мечту Физо - уточнить метод определения скорости течения воды. Для создания стационарного потока использовался амстердамский водопровод; давление жидкости тщательно регулировалось. Расхождение результатов Зеемана с расчетом по формуле Френеля не превышало 2,6%.
Для решения вопроса о влиянии дисперсии света на результаты опытов Зееман и его сотрудники исследовали распространение света в движущихся твердых телах, изготовленных из материалов, характеризующихся значительной дисперсией. Ко времени проведения опытов выдающийся голландский физик X. Лоренц (1853-1928) получил выражение для коэффициента увлечения с учетом дисперсии:
| μ′ = 1 - | 1 | - | λ | dn | |
| n2 | n | dλ |
которое при малой дисперсии
| ( | dn | → 0) |
| dλ |
дает френелевский коэффициент μ = 1 - 1/n2. Теория Лоренца была построена на основе представлений об электронном строении материи и считалась более физически обоснованной, чем теория Френеля.
В опытах группы Зеемана цилиндры из специального стекла - флинта и из кварца приводились в движение со скоростью около 10 м/с с помощью кривошипно-шатунного механизма. Интерференционная картина фотографировалась при движении цилиндров слева направо, а затем - при обратном движении, после чего проводилось сравнение положения полос. Измерения проводились в трех узких интервалах длин волн: 4750 Aº, 5380 Аº, 8510 Аº. Высокая точность эксперимента позволила обнаружить влияние дисперсии на результаты опыта и подтвердить формулу Лоренца.
Еще одна проблема оптики движущихся тел, разрешить которую опыт Физо не мог, состояла в следующем. В эксперименте Физо было доказано наличие влияния движения воды (или, как говорили в XIX в., "весомой материи") на распространение света. Но свет может распространяться и в вакууме, который, согласно представлениям физиков прошлого века, заполнен эфиром. Можно ли каким-либо образом зафиксировать движение наблюдателя относительно эфира, если измерения проводятся в среде с коэффициентом преломления, близким к единице?
Этот вопрос непосредственно касается принципа относительности. Еще в XVII в. было сформулировано утверждение (так называемый принцип относительности Галилея) о том, что все механические процессы происходят одинаково во всех инерциальных системах отсчета, движущихся друг относительно друга равномерно и прямолинейно. Математическим выражением этого утверждения является инвариантность уравнений ньютоновской механики по отношению к преобразованиям Галилея, связывающим пространственные и временные координаты в двух инерциальных системах отсчета.
После создания электродинамики Максвелла естественно встал вопрос: справедлив ли принцип относительности применительно к электродинамике? В отличие от уравнений механики, максвелловские уравнения меняли свой вид при преобразованиях Галилея. Кроме того, из них, например, следовало, что скорость распространения электромагнитных волн в вакууме (т. е. скорость света) не зависит от движения источника и наблюдателя. Это следствие теории Максвелла находилось в вопиющем противоречии с классическим правилом сложения скоростей - следствием принципа относительности Галилея.
Предлагались различные решения возникшей проблемы. Немецкий физик Генрих Герц (1857-1894) предложил свою версию электродинамики, основанную на гипотезе о полном увлечении эфира движущимися телами. Уравнения Герца были инвариантны по отношению к преобразованиям Галилея. Таким образом, Герц попытался распространить классический принцип относительности на электромагнитные явления, отказавшись от уравнений Максвелла. Однако теория Герца явно противоречила результатам опыта Физо и не была принята физиками.
Альтернативное решение проблемы состояло в предположении, что в вакууме существует покоящийся эфир, который можно было бы принять за абсолютную систему отсчета, отказавшись тем самым от принципа относительности в электродинамике и, следовательно, в оптике.
Ответить на вопрос о существовании неподвижного эфира мог только опыт. Но постановка соответствующих опытов требовала преодоления гигантских экспериментальных трудностей, на которые указывал еще Максвелл. В статье "Эфир", написанной для Британской энциклопедии, он писал:
"Если бы можно было определить скорость света, наблюдая время, употребляемое им на прохождение от одного пункта до другого на поверхности Земли, то, сравнивая наблюдаемые скорости движения в противоположных направлениях, мы могли бы определить скорость эфира по отношению к этим земным пунктам. Но все методы, которые можно применить к нахождению скорости света из земных опытов, зависят от измерения времени, необходимого для двойного перехода от одного пункта до другого и обратно (курсив наш. - С. Ф.) и увеличение этого времени вследствие относительной скорости эфира, равной скорости Земли на ее орбите, составило бы всего около одной стомиллионной доли всего времени перехода и было бы, следовательно, совершенно незаметно.
...Единственный возможный способ прямого определения относительной скорости эфира по отношению к Солнечной системе заключается в сравнении значений скорости света, выведенных из наблюдений затмений спутников Юпитера, когда Юпитер виден с Земли приблизительно в противоположных точках эклиптики".
Однако даже сейчас точность астрономических наблюдений не позволяет зарегистрировать эффект, о котором говорил Максвелл.
Таким образом, приходится рассчитывать только на проведение "земных" экспериментов, в которых свет проходит замкнутый путь. Максвелловскую оценку необходимой точности опыта можно получить из следующих простых рассуждений. Допустим, что эфир неподвижен, а скорость движения Земли параллельна отрезку, соединяющему две точки на поверхности Земли. Если расстояние между этими точками равно l, то полное время движения света от одной точки до другой и обратно равно
| t1 = | l | + | l | = | 2lc | . |
| с - υ | c + υ | c2 - υ2 |
Если бы движение Земли не оказывало влияния на распространение света, это время определялось бы выражением
| t2 = | 2l | , |
| c |
поэтому для экспериментального решения проблемы требуется зафиксировать время движения света с точностью, большей, чем разность
| Δt = t1 - t2 = | 2l | υ2 | . | |
| c | c2 |
Отсюда следует и оценка Максвелла:
| Δt | = | υ2 | |
| t2 | c2 |
Скорость движения Земли по орбите составляет около 30 км/с, поэтому
| Δt | ≈ 10-8. | |
| t2 |
Таким образом, относительная точность "земных" опытов для обнаружения движения Земли по отношению к неподвижному эфиру должна намного превосходить относительную точность соответствующих астрономических измерений. В земных условиях требовалось проведение опытов с точностью, превосходящей квадрат отношения скорости движения Земли к скорости света, поэтому физики стали говорить о необходимости исследования эффектов "второго порядка".
За эту труднейшую задачу взялся Майкельсон. Он решил обнаружить "эфирный ветер", который должен возникать при движении Земли относительно неподвижного эфира. Его исследования в этой области начались еще в 1880 г. в Берлине, когда ученый работал в лаборатории Г. Гельмгольца.
Майкельсон понимал, что для проведения опытов со столь высокой точностью вряд ли достаточно ограничиться совершенствованием существующих оптических схем. Он предложил собственную схему интерферометра, с помощью которого надеялся добиться успеха. Принципиальная схема интерферометра показана на рис. 24, а.
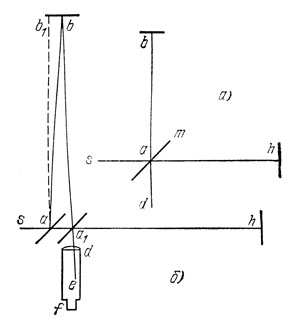
Рис. 24. а) Ход лучей в интерферометре Майкельсона. б) К расчету разности хода лучей в интерферометре Майкельсона
Луч света sa от какого-либо источника падает на полупрозрачную пластинку m и частью проходит к зеркалу h, а частью отражается в перпендикулярном направлении к зеркалу b. Отразившись от зеркала b, луч проходит через полупрозрачную пластинку по направлению ad; по тому же направлению отражается от пластинки луч, возвращающийся от зеркала h. Поскольку оба луча, идущие вдоль направления ad, образованы из одного луча sa, они могут интерферировать. Интерференционную картину, образованную ими, можно рассматривать при помощи зрительной трубы. Понятно, что в случае, когда зеркала h и b расположены строго перпендикулярно друг к другу и падающим на них лучам, в зависимости от разности хода лучей, приходящих от разных зеркал, в зрительной трубе будет наблюдаться более или менее светлое пятно. В этом описании существенно предположение о том, что интерферируют именно лучи, т. е. очень узкие пучки света. При использовании широких пучков в зрительной трубе должны быть видны концентрические чередующиеся темные и светлые кольца - так называемые полосы равного наклона. В реальной установке, однако, картина концентрических колец не наблюдается, поскольку невозможна абсолютно точная настройка зеркал. В поле зрения трубы интерферометра видны параллельные чередующиеся темные и светлые полосы - полосы "равной толщины". Их происхождение сродни происхождению интерференционных полос, возникающих при отражении параллельного пучка света от вертикально расположенной мыльной пленки. Малейшие изменения условий распространения лучей до зеркал и обратно приводят к сдвигу интерференционной картины.
Идея опыта, задуманного Майкельсоном, состоит в следующем (рис. 24, б). Пусть сначала интерферометр ориентирован таким образом, что луч ah параллелен скорости движения Земли по орбите, а луч аb1 - перпендикулярен ей. Тогда, согласно представлениям о неподвижном эфире, луч sa отразится вдоль аb, причем тангенс угла b1ab будет равен υ/c (так как υ << c, тангенс этого угла можно считать равным самому углу), а возвращающийся луч пойдет по направлению bа1 (угол aba1 ≈ 2υ/c). Луч ah вернется от зеркала h по прежнему направлению, но, отразившись от движущейся в эфире полупрозрачной пластинки m в точке а1 пойдет по направлению а1е. При этом угол
| ha1e = | π | - bab1 = | π | - | υ |
| 2 | 2 | c |
и, следовательно, второй луч пойдет в одном направлении с первым.
Найдем разность оптических путей aba1 и aha1 если длина плеч интерферометра в точности одна и та же и равна D. Время, необходимое для прохождения светом пути от а к h и обратно, равно
| t1 = | 2Dc | . |
| c2 - υ2 |
Путь, проходимый светом за это время в неподвижном эфире, равен l1 = t1c ≈ 2D(1 + υ2/c2). Величина l1 в последней формуле определена с точностью до величины четвертого порядка относительно υ/c; мы воспользовались соотношением (1 + x)α ≈ 1 + ах, если x << 1. Нетрудно видеть, что путь другого луча равен
| l2 = 2D√(1 + | υ2 | )≈ 2D(1 + 1/2 | υ2 | ) |
| c2 | c2 |
Таким образом, вследствие движения в неподвижном эфире между лучами должна возникать разность хода
| l1 - l2 = D | υ2 | . |
| c2 |
Теперь представим себе, что интерферометр медленно поворачивается вокруг вертикальной оси, проходящей через середину пластинки m. Условия движения света при вращении установки будут меняться и, следовательно, должна меняться картина интерференции: полосы в поле зрения зрительной трубы будут сдвигаться. В частности, при повороте интерферометра на 90° относительно первоначального положения разность хода между двумя лучами будет составлять уже
| - D | υ2 | . |
| c2 |
Значит, максимальное смещение интерференционной полосы определяется изменением разности хода лучей на
| 2D | υ2 | . |
| c2 |
По замыслу Майкельсона экспериментатор должен был несколько раз в день фиксировать положение полос интерференции при различных ориентациях плеч интерферометра.
Первый интерферометр, изготовленный по чертежам Майкельсона на инструментальном заводе в Берлине на средства Александра Белла - создателя телефона, показан на рис. 25. В качестве источника света использовался специальный осветитель; это позволяло работать в монохроматическом свете (желтая линия натрия λ = 5890 А). Длина плеч интерферометра составляла D = 120 см. Из рис. 25 видно, что на столике укреплена не одна, а две пластины. Вторая пластина m′ вырезалась из того же куска стекла, что и пластина m, однако, в отличие от нее, была полностью прозрачной. И пользование дополнительной пластины связано с необходимостью скомпенсировать разность хода, возникающую из-за того, что одному из лучей приходится дважды проходить через полупрозрачную пластину, а другому - только один раз (в расчете толщина этой пластины не учитывалась).
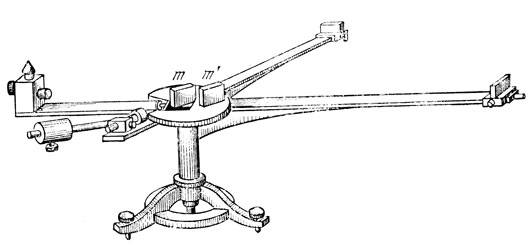
Рис. 25. Внешний вид первого интерферометра Майкельсона. m - полупрозрачная пластина, m′ - пластина-компенсатор
Первое испытание интерферометр Майкельсона прошел в лаборатории Гельмгольца. Руководитель лаборатории при обсуждении будущего эксперимента выразил опасения, что трудности поддержания постоянной температуры установки могут помешать успешному проведению опытов. Майкельсон возразил, что для поддержания постоянной температуры требуется всего лишь... окружить установку тающим льдом. При первых же опытах выяснилось, что основная опасность таилась не в колебаниях температуры, а в вибрациях, к которым прибор был очень чувствителен: он реагировал даже на вибрации, создаваемые экипажами, проезжающими по улицам Берлина. Установку пришлось перевезти в астрономическую обсерваторию в Потсдам. Там она была смонтирована в нише кирпичного фундамента большого телескопа. Только после этого Майкельсон получил возможность провести первые измерения. Впрочем, и на новом месте прибор реагировал на шаги человека, идущего по каменной мостовой в квартале от обсерватории.
Каков же был результат опытов? Отрицательный - смещение полос, которое можно было бы связать с "эфирным ветром", обнаружить не удалось. Однако можно ли было с помощью первого прибора Майкельсона обнаружить искомый эффект? Для ответа на этот вопрос требуется уточнить характеристики этого интерферометра. Расстояние между двумя соседними полосами занимало 3 деления шкалы, видимой глазом в оптическую трубу. Положение центра темной полосы можно было фиксировать с точностью до 1/4 деления шкалы. В итоге точность, с которой можно было определить смещение полосы, составляла 1/12 ширины полосы. Нетрудно рассчитать, что ожидаемый сдвиг полосы, связанный с изменением разности хода при вращении установки, равен 2Dυ2/(λс2) ≈ 0,04. Таким образом, ожидаемое смещение в два раза меньше точности измерений. Опыт недоказателен! Тем не менее Майкельсон опубликовал результаты опытов и даже решился сформулировать вывод: "Гипотеза эфира ошибочна".
На этом закончился европейский цикл экспериментов Майкельсона. В 1882 г. ученый вернулся в США и начал работать во вновь открытой школе прикладной науки Кейса. Здесь он принялся за организацию научной лаборатории - именно в ней он провел исследования, обосновавшие применимость к свету представлений о фазовой и групповой скоростях. Работая в школе Кейса, Майкельсон сблизился с профессором химии университета "Уэстерн Резерв" Эдвардом Морли (1838-1923). Когда под влиянием Рэлея и В. Томсона Майкельсон решил снова обратиться к проблеме эфира, он, не колеблясь, предложил Морли сотрудничество.

Альберт Майкельсон (1852-1931)
Первым научным результатом, полученным Майкельсоном и Морли, было уже упоминавшееся подтверждение выводов Физо о распространении света в движущихся средах. После окончания этих опытов коллеги взялись за повторение потсдамского эксперимента.
Однако повторялась лишь идея - вся установка была создана заново. Она представляла для своего времени шедевр экспериментального искусства.
На рис. 26 показана установка Майкельсона и Морли в разрезе. Интерферометр был собран в подвальном помещении. Его основные части были смонтированы на массивной каменной плите площадью около 150 кв. см и толщиной 30 см. Для сохранения горизонтальности плиты она располагалась на деревянном поплавке. Сам поплавок плавал в кольцеобразном чугунном сосуде, толщина стенок которого была около 1,5 см, заполненном очищенной ртутью. Использование жидкой ртути позволило практически избавиться от влияния вибраций, доставивших столько хлопот Майкельсону при проведении опытов в Европе. Деревянный поплавок и каменная плита насаживались на осевой стержень. Этот стержень обеспечивал соосность чугунного сосуда и поплавка. Чугунный сосуд покоился на опоре - кирпичном восьмиграннике, залитом цементом. Основанием установки служил фундамент, уходивший вниз, под землю, и достигавший коренных пород. По окружности сосуда были сделаны 16 отметок, позволявших фиксировать ориентацию плиты.
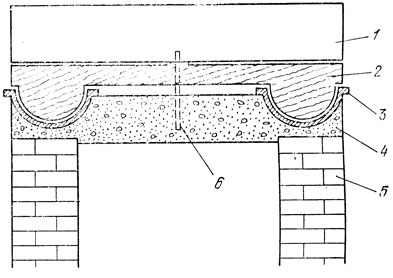
Рис. 26. Установка Майкельсона - Морли. 1 - каменная плита, 2 - деревянный поплавок, 3 - сосуд, заполненный ртутью, 4 - цементное основание, 5 - фундамент, 6 - осевой стержень

Эдвард Морли (1838-1923)
Внешний вид самого интерферометра показан на рис. 27, а, ход лучей в нем - на рис. 27, б. Для того чтобы увеличить общий путь лучей до зрительной трубы, использовалась система зеркал: по четыре круглых зеркала, изготовленных из сплава олова, меди и мышьяка, на каждом углу. В итоге общая длина пути каждого из лучей составляла около 11 м, т. е. была примерно в 10 раз больше, чем в первом эксперименте. Оптическая система интерферометра была защищена от внешних воздействий деревянным кожухом (на рис. 27 он не показан).
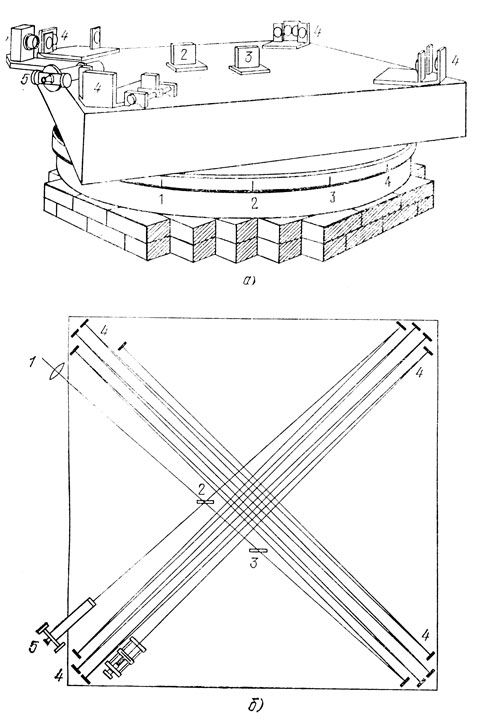
Рис. 27. а) Внешний вид интерферометра Майкельсона - Морли. б) Ход лучей в интерферометре. 1 - источник света, 2 - делительная пластинка, 3 - пластинка-компенсатор, 4 - система зеркал, 5 - зрительная труба
На регулировку прибора ушло несколько месяцев. Наконец, ученые смогли приступить к измерениям. Поскольку, плита плавала в ртути, то под действием небольшого толчка она приходила в плавное, медленное вращение. Один полный оборот совершался примерно за 6 минут. Наблюдатель ходил вокруг аппарата, перемещаясь одновременно с плитой и периодически измеряя положение полос. Майкельсон и Морли проводили измерения два раза в день - в полдень и в шесть часов вечера, определяя положение полос при 16 ориентациях интерферометра. Новый интерферометр позволял производить измерения очень малых сдвигов полос - ширина одной полосы соответствовала 50 делениям измерителя, т. е. можно было определить смещение полос, составлявшее 0,01 их ширины.
Обработанные результаты измерений, законченных в 1887 г., представлены на рис. 28. Из графиков видно, что наблюдаемое смещение составляет не более 1/20 теоретического, а, вероятно, и менее 1/40. Видимые систематические смещения полос можно отнести за счет периодических колебаний температуры, давления и других внешних факторов, влияние которых полностью устранить не удается.
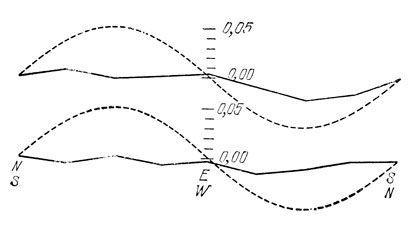
Рис. 28. Результаты измерений Майкельсона и Морли. На графике отложены смещения полос (выраженные в долях ширины полосы) в зависимости от ориентации интерферометра. Кривая, рассчитанная на основе теории неподвижного эфира, дана прерывистой линией (ее ординаты уменьшены в 8 раз). Сплошная линия соединяет экспериментальные точки, полученные для разных ориентации интерферометра. Верхний график соответствует полуденным наблюдениям, нижний - вечерним
Результат опыта Майкельсона - Морли однозначно свидетельствовал об ошибочности гипотезы неподвижного эфира. Этот вывод взбудоражил научный мир. Он потребовал пересмотра важнейших представлений физики. Для объяснения отсутствия эффекта "эфирного ветра" Лоренц и Фитцджеральд независимо выдвинули гипотезу о сжатии всех материальных тел в направлении движения. Хотя гипотеза Лоренца - Фитцджеральда не имела под собой надежного физического обоснования, ее появление свидетельствовало о том, что результаты опыта Майкельсона - Морли стали фундаментальным критерием истинности любой физической теории, касавшейся свойств пространства и времени.
Сообщение о полученных результатах Майкельсон и Морли послали в "Американский научный журнал". Оно называлось "Об относительном движении Земли и светоносного эфира". Вскоре из разных стран стали поступать отклики на публикацию. Далеко не все с энтузиазмом отнеслись к выводам американских физиков. Прежде всего возникли сомнения в правильности интерпретации полученных данных. Можно ли пользоваться упрощенными рассуждениями, подобными тем, которыми пользовались мы для расчета запаздывания одного из лучей? Некоторые физики, вероятно, вспоминали, что еще в своей первой публикации по проблеме эфира, в 1881 г. Майкельсон допустил ошибку, вследствие чего получил величину запаздывания, завышенную в два раза. Нет ли ошибки и в его новой работе? Тщательно проверялось возможное влияние на исход опыта разнообразных факторов: ширины пучка света, положения зеркал и разделительной пластинки, отражения от движущихся зеркал, монохроматичности и т. д. Хотя в конце концов была установлена справедливость упрощенной интерпретации опыта, данной Майкельсоном, Лоренц спустя шесть лет после проведения эксперимента писал Рэлею:
"Я в чрезвычайном затруднении относительно того, как разрешить это противоречие (т. е. отрицательный результат опыта. - С. Ф.), и тем не менее я думаю, что если бы нам пришлось отказаться от теории Френеля, у нас вообще не осталось бы приемлемой теории... Не может ли быть некоторого пункта в теории опыта мистера Майкельсона, который до сих пор не был замечен?"
Лорд Кельвин рассматривал результат опыта как одно из облаков, затемнявших "красоту и ясность динамической теории, которая рассматривала теплоту и свет как виды движения". Рэлей назвал этот результат "истинным разочарованием".
Даже сам Майкельсон был явно обескуражен полученными данными. Спустя много лет он напишет:
"Эксперимент кажется мне исторически ценным уже тем, что для решения этой проблемы был изобретен интерферометр. Я думаю, будет признано, что изобретение интерферометра более чем скомпенсировало тот факт, что этот частный эксперимент дал отрицательный результат".
Отражением общего отношения к результатам опыта была формулировка Нобелевского комитета, присудившего Майкельсону премию (1907 г.) "За создание прецизионных оптических инструментов и выполнение с их помощью спектроскопических и метрологических экспериментов". И ни слова о важнейшем опыте лауреата!
Впрочем, принципиальный характер опытов, посвященных поискам "эфирного ветра", был ясен, и попытки его обнаружения не прекращались. Сам Майкельсон проверил гипотезу о том, что Земля в своем движении почти полностью увлекает эфир, так что его относительная скорость вблизи поверхности Земли мала или равна нулю. В середине 90-х годов XIX в. он наблюдал интерференцию двух пучков света, прошедших по периметру вертикально поставленного прямоугольника, стороны которого были равны 15 и 60 м. Полученные результаты не подтвердили первоначальное предположение.
Огромную работу по проверке результатов опыта Майкельсона - Морли проделал профессор школы Кейса Д. С. Миллер. Начиная с 1897 г. он, сначала совместно с Морли, а затем в одиночку в течение почти тридцати лет пытался опровергнуть вывод о крушении теории неподвижного эфира. Ряд его данных позволил противникам теории относительности в конце 20-х годов XX в. утверждать, что теория Эйнштейна несостоятельна. Однако впоследствии была доказана ошибочность выводов Миллера.
В 1922 г. молодой американский физик Р. Кеннеди внес ряд усовершенствований в установку Майкельсона. Однако повышение точности опыта привело лишь к тому, что было зарегистрировано смещение полос интерференции на 0,001 часть ее ширины, в то время как ожидаемое смещение должно было составлять 0,07 ширины полосы. Экспериментальное искусство Кеннеди получило высокую оценку самого Майкельсона. "Я вижу, что напрасно тратил время, - сказал он Кеннеди. - Если бы я знал, что вы сделаете это так хорошо, я не стал бы заниматься тем же самым."
В конце 20-х годов XX в. швейцарский физик А. Пикар и бельгиец Е. Стэль повторили опыт Майкельсона - Морли с помощью специального малогабаритного интерферометра, подвешенного к воздушному шару, который поднимался на высоту 2,5 км (рис. 29). Интерференционная картина фотографировалась автоматически при равномерном вращении шара, создаваемом маленькими пропеллерами. И в этом случае не удалось обнаружить "эфирный ветер".
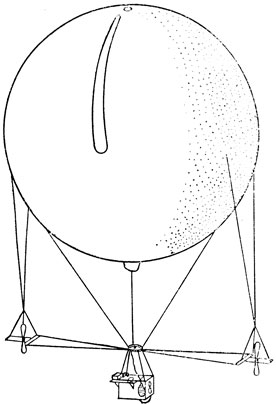
Рис. 29. Воздушный шар Пикара с установкой для проведения опыта Майкельсона
Определенные итоги поисков "эфирного ветра" подвела конференция, созванная в обсерватории Маунт Вильсон в США, где некоторое время работал Майкельсон. Она проходила 4 и 5 февраля 1927 г. В ней, кроме самого Майкельсона, принимали участие Лоренц, Миллер, Кеннеди и ряд других известных физиков. В целом конференция способствовала укреплению позиций теории относительности, поскольку на ней не было приведено каких-либо серьезных доказательств, ставящих под сомнение отрицательные результаты многочисленных повторений опыта Майкельсона - Морли.
Впоследствии опыт Майкельсона повторялся еще не один раз. Повышение его точности достигалось за счет использования новой физической аппаратуры: генераторов излучения сверхвысоких частот (СВЧ), мазеров, лазеров и т. д. Одна из позднейших попыток обнаружения "эфирного ветра" показала, что отношение скорости света в направлении движения Земли к скорости света в направлении, перпендикулярном к этому движению, отличается от единицы не более, чем на 10-15. Это на сегодняшний день наиболее точное повторение опыта, давшего, по словам английского физика и философа Дж. Бернала, "величайший из всех отрицательных результатов в истории науки".
* * *
Мы подробно рассмотрели экспериментальный аспект проблемы поиска "эфирного ветра". В чем же состоит значение полученных отрицательных результатов для физической теории?
Естественное объяснение результаты опыта Майкельсона - Морли получили в 1905 г. после выхода в свет работы Альберта Эйнштейна (1879-1955) "К электродинамике движущихся тел", в которой были изложены основы специальной теории относительности (СТО).
В отличие от своих предшественников, Эйнштейн не строил гипотез о влиянии движения тел на эфир. Он поступил смело и решительно: вовсе отказался от рассмотрения эфира как физического объекта. В основу теории он положил два постулата. Первый, именуемый принципом относительности, в современной формулировке звучит так:
"Все физические явления в инерциальных системах отсчета при одинаковых начальных условиях протекают одинаково".
По существу, этот постулат представляет собой распространение принципа относительности Галилея на все явления природы. Хотя результаты, полученные Майкельсоном и Морли, по-видимому, не сыграли решающей роли в создании Эйнштейном СТО, они явились важным фактором в признании этой теории многими физиками. Отсутствие "эфирного ветра" говорит о том, что не существует выделенной, абсолютной системы отсчета и указывает на применимость принципа относительности к электродинамике. Именно в этом состоит основное значение опыта Майкельсона - Морли.
Второй постулат Эйнштейна звучит так:
"Скорость света в пустоте во всех инерциальных системах отсчета одинакова, причем одинакова по всем направлениям и не зависит ни от скорости источника, ни от скорости наблюдателя". Именно этот постулат вызвал наиболее острые дискуссии после появления работы Эйнштейна. Необходимо подчеркнуть, что результаты опыта Майкельсона - Морли не являются подтверждением этого постулата в целом. В этом опыте источник неподвижен относительно наблюдателя, поэтому опыт не может ничего сказать о зависимости или независимости скорости света от движения источника и наблюдателя.
Второй постулат находится в очевидном противоречии с классическим правилом сложения скоростей. Физики так привыкли к этому правилу, что никак не могли смириться с его ограниченностью*. Уже после появления работы Эйнштейна были сделаны попытки построить согласующиеся с опытом теории, в которых сохранялся принцип относительности, а второй постулат СТО был заменен другим, более "привычным". Так, швейцарский физик В. Ритц (1878-1909) в 1908 г. выдвинул так называемую "баллистическую" гипотезу. Согласно этой гипотезе по отношению к неподвижному наблюдателю скорость света, испускаемого движущимся источником, больше скорости света, испускаемого неподвижным источником, на величину скорости источника. При этом Ритц, конечно, вынужден был отказаться от уравнений Максвелла. Однако теория Ритца успеха не имела. Она была опровергнута астрономическими наблюдениями, выполненными в 1913 г. голландским астрономом В. де Ситтером (1872-1934).
* (Классическим правилом сложения скоростей можно пользоваться, если скорости-слагаемые по величине много меньше скорости света. )
Астрономам давно известны так называемые двойные звезды - системы из двух звезд, обращающихся вокруг общего центра масс. Для того чтобы понять, в чем состоит идея опровержения баллистической гипотезы, рассмотрим одну из звезд двойной системы. Пусть эта звезда движется по орбите, близкой к круговой (рис. 30). Если верна теория Ритца, то свет, идущий от звезды, находящейся в точке A, доходит до Земли за время
| t1 = | L | , |
| c + υ |
где L - расстояние от звезды до Земли, υ - линейная скорость звезды на орбите. Свет, испущенный звездой в точке В, дойдет до Земли за время
| t2 = | L | . |
| c - υ |
Обозначим через Т период полуобращения звезды, тогда период полуобращения, измеренный по наблюдениям с Земли как время видимого движения звезды от А до В, равен
| Т + | 2Lυ | ; |
| с2 - υ2 |
соответствующий период, измеренный при движении звезды от В до A, равен
| Т - | 2Lυ | . |
| с2 - υ2 |
Поскольку расстояния до звезд очень велики, величина
| 2Lυ | |
| с2 - υ2 |
может быть сравнима с T даже при выполнении условия υ << c. Отсюда следует, что если гипотеза Ритца справедлива, то при наблюдениях с Земли в движении звезд в двойных системах должны регистрироваться отклонения от законов Кеплера. В действительности таких отклонений не наблюдается. Это свидетельствует против гипотезы о сложении скорости звезды со скоростью света. Де Ситтер с учетом точности имевшихся в то время астрономических наблюдений показал, что если скорость света в системе наблюдателя с′ представить в виде суммы c′ = c + kυ, то можно утверждать, что k < 0,02. Выдающийся швейцарский физик В. Паули в своей книге "Теория относительности" писал, что эти данные "позволяют почти с достоверностью считать правильным положение о постоянстве скорости (света. - С. Ф.), а теории истечения Ритца и других признать ведущими к непреодолимым затруднениям".
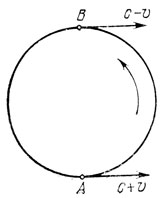
Рис. 30. К расчету запаздывания света по Ритцу
Проводились и другие опыты для проверки второго постулата СТО. Так, в 1923 г. Р. Томашек провел измерения по схеме Майкельсона - Морли, но в качестве источника света использовал движущиеся астрономические объекты (Солнце, Луну, Юпитер, Сириус, Арктур). Наблюдавшиеся смещения полос интерференции составляли не более 1/8 теоретически ожидаемых.
Опыты по проверке второго постулата продолжаются и в наши дни; для их проведения используются новейшие достижения физической науки и техники.
Пристальное внимание к постулатам специальной теории относительности (СТО), проявленное учеными в начале XX в. и не ослабевающее до сих пор, объясняется теми неожиданными и необычными выводами, к которым привела СТО. Из анализа пространственно-временных соотношений между событиями, регистрируемыми в разных системах отсчета, Эйнштейн сделал вывод о необходимости заменить классическое правило сложения скоростей новым правилом: если одна инерциальная система (К′) движется относительно другой (К) со скоростью υ, то сигнал, распространяющийся в системе К со скоростью u вдоль направления относительного движения двух систем, с точки зрения наблюдателя, неподвижного в системе K, будет двигаться со скоростью
| u′ = | u + υ | (VI. 2) |
| + uυ/c2 |
(считается, что сигнал в системе К движется навстречу движению системы К′). Анализируя этот закон, Эйнштейн обратил внимание на то, что ни в одной инерциальной системе отсчета невозможно распространение сигнала со скоростью, большей скорости света в пустоте. Действительно, нетрудно убедиться, что даже если u = с, то u′ = с. Надо отметить, что этот вывод, в принципе, не является чисто логическим следствием СТО. Эйнштейн, рассматривая возможность передачи сигналов со, скоростью, большей скорости света в пустоте, писал, что в этом случае "...мы вынуждены считать возможным механизм передачи сигнала, при использовании которого достигаемое действие предшествует причине. Хотя этот результат с чисто логической точки зрения и не содержит, по-моему, в себе никаких противоречий, он все же настолько противоречит характеру всего нашего опыта, что невозможность предположения υ > c представляется в достаточной степени доказанной". Таким образом, вывод Эйнштейна базируется на принципе причинности, который является обобщением всего нашего опыта.
Это не значит, однако, что в рамках СТО невозможны скорости, превосходящие с. Рассмотрим распространение светового импульса из точки О к точкам А и В (рис. 31). Допустим, что расстояния ОА и ОВ столь велики, что фронт импульса вблизи А и В можно считать плоским. На рисунке прерывистыми линиями 1, 2 и 3 показано положение фронта импульса для трех последовательных промежутков времени t1 < t2 < t3. Видно, что импульс сначала достигает точки А (положение 1). Дальнейшее распространение импульса можно рассматривать как его движение от А к В со скоростью υ = c/cosφ (мы следим за перемещением точки пересечения фронта импульса и прямой, соединяющей А и B). Легко видеть, что при таком подходе скорость импульса превосходит с тем больше, чем ближе φ к π/2. Импульс, бегущий от А к B, вполне реален: если поместить на пути от A к В какой-либо рассеиватель света, то попадание на него импульса будет сопровождаться вспышкой света, которую можно зарегистрировать. Однако никакого противоречия со специальной теорией относительности рассмотренный пример не содержит. СТО запрещает не любое движение со сверхсветовой скоростью, а лишь передачу сигнала со скоростью, большей с. В нашем примере импульс, приходящий от А к В, не несет никакой информации о точке A, и не может рассматриваться как сигнал из точки A.
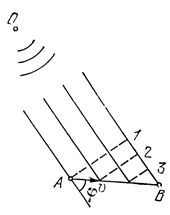
Рис. 31. Короткий световой импульс, источником которого служит точка О, достигнув точки A, бежит вдоль прямой АВ со скоростью υ = c/cosφ
И все же сказать, что вопрос о том, является ли скорость света в пустоте предельной скоростью распространения сигналов окончательно решен, по-видимому, нельзя. Последние пятнадцать лет на страницах научных журналов идет обсуждение проблемы, касающейся существования частиц, движущихся со сверхсветовыми скоростями. Наибольшей известностью пользуются гипотетические частицы с мнимой массой, которым американский физик Дж. Фейнберг дал название "тахионы"*. Проделана большая теоретическая работа по анализу следствий "тахионной гипотезы". Сделаны попытки объяснить результаты ряда экспериментов существованием "сверхсветовых" частиц. Однако приходится констатировать, что на сегодняшний день реальность этих объектов не доказана. С другой стороны, никто пока не опроверг идею о тахионах...
* (От греческого слова tachys - быстрый.)
|
ПОИСК:
|