Великая теорема Карно

Уточним рассуждения о цикле Карно. Если попытаться произвести все операции не мысленно, а на самом деле, то мы обнаружим, что часть тепла будет тратиться на нагревание стенок цилиндра, на неравномерное движение поршня и т. д. "Вредные" потери будут тем больше, чем больше разность температур между газом и внешней средой и чем больше скорость движения поршня. Поэтому будем предполагать, что поршень движется очень медленно и что разность температур, например, между газом и нагревателем очень мала. Это, конечно, не выполняется в реальных машинах, так как при таких условиях машина работала бы бесконечно медленно и ее мощность равнялась бы, строго говоря, нулю.

Но мы, следуя за Карно, ищем условия для получения максимальной работы, и нам придется примириться с тем, что такая работа производится установкой с мощностью, равной нулю.

Нетрудно видеть, что так как в цикле не происходит? потерь, то все операции - а их всего четыре - можно произвести в обратном порядке. Если обозначить этапы буквами α β,γ, δ, то цикл Карно можно записать так: С=βγδ (формулу надо читать справа налево).

Обратные операции мы обозначим буквами α^-1, β^-1, γ^-1, δ^-1. Так, операция α отвечает движению по изотерме от точки a до точки б, a α^-1 отвечает обратному движению - от б к а. Если мы произведем последовательно опeрации α и α^-1, то, очевидно, вернем газ в исходное состояние. Это мы запишем так: α^{-1 α=1.}

Итак, цикл С мы можем в идеальном случае произвести в обратном порядке. Обозначим такой обратный цикл через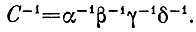

Ясно, что

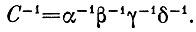
Это означает просто, что, проведя цикл С, а затем цикл С^-1, мы вернем все в исходное состояние: нагреватель получит обратно свою порцию тепла Q₁ от холодильника будет отобрано тепло Q₂, и на все это будет затрачена вся работа, выигранная в прямом цикле.

Обратный цикл C_-1 совсем не обязательно должен состоять из тех же этапов, что и прямой. Надо только, чтобы он возвращал систему из конечного состояния в начальное.

Докажем теперь, что не существует тепловой машины, которая была бы менее выгодной, чем машина, использующая цикл Карно.

Предположим, что кто-то такую тепловую машину придумал. Тогда с ее помощью можно реализовать обратный цикл С^-11, потратив на это всю работу, полученную в прямом цикле. Менее выгодная машина будет забирать от нагревателя больше тепла и больше отдавать холодильнику. Тогда потратив всю работу, полученную в прямом цикле (цикл Карно), мы отберем у холодильника больше тепла и передадим больше тепла нагревателю. В результате двух циклов холодное тело потеряло тепло - холодильник охладился, а нагреватель нагрелся - при-обрел тепло. Рабочее же тело, как обычно в круговом процессе, вернулось не изменившимся в исходное состояние, Процесса такого рода - "бесплатного" переноса тепла от холодильника к нагревателю - в природе быть не может; не может быть, следовательно, и цикла более эффективного, чем цикл Карно.

Наш вывод полезно повторить с помощью рисунка (см. рис. 10, а). Верхний горизонтальный отрезок - это нагреватель; нижний - холодильник. Стрелки показывают, что от нагревателя взято тепло Q₁, а холодильнику отдано Q₂. ПО закону сохранения энергии разность Q₁-Q₂ есть работа А, полученная за один цикл. Это значит, что разность Q₁-Q₂ (при заданной работе) имеет определенное значение, в то же время величина Q₁ (или Q₂ ) ничем не определена и ее можно изменять. Следовательно, у разных машин Q₁ могло быть либо больше, либо меньше тепла, затраченного нагревателем в цикле Карно. Но такое заключение, как мы видели, приводит к противоречию.

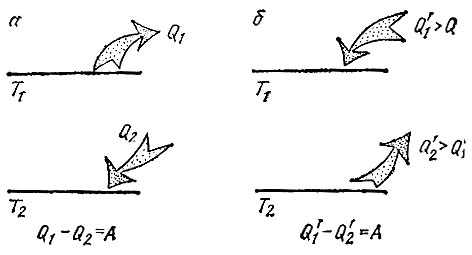
Рис. 10

На рис. 10, б изображен такой цикл D с Q₁ большим, чем в цикле Карно (т. е. цикл, производящий работу за счет большего количества теплоты, взятого у нагревателя,- конечно, разность Q^'₁-Q^'₂ остается той же, т. е. в цикле и Q₂ больше, чем в цикле Карно). Такой цикл работает (по предположению) менее эффективно, чем цикл Карно, так как из Q^'₁>Q₁ следует, что

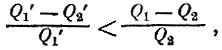
поскольку числители у обеих дробей одинаковые.

Таким образом, с помощью нового цикла можно было бы перенести в нагреватель из холодильника больше тепла, чем было отнято у нагревателя в прямом цикле.

Следовательно, мы перенесем тепло Q^'₁>Q₁ от холодильника к нагревателю. Отсюда и вывод, сделанный выше.

Также невозможно, чтобы цикл D был более эффективным, чем цикл С. Доказательство просто повторяет предыдущее, только надо в качестве прямого цикла выбрать цикл D, а обратного цикла - цикл С. В цикле С от холодильника будет перенесено больше тепла, чем было перенесено к холодильнику в прямом цикле D.

При обсуждении мы использовали обратимость циклов: если в прямом цикле переносится определенное количество теплоты при совершении работы, то в обратном цикле затрата той же работы совершается обратным переносом того же количества теплоты. Для этого важно, чтобы циклы были идеальными, ибо потери в прямом цикле, естественно, не возмещаются в обратном!

Итак, хотя формально количества теплоты Q₁ и Q₂ как будто бы ограничены лишь условием Q₁-Q₁=A, но предположение, что они могут быть разные в разных (обратимых) циклах, приводит к нарушению принципа, получившего название второго начала термодинамики:

Невозможно осуществить процесс, в результате которого тепло было бы перенесено от холодного тела к горячему без совершения работы.

Второе начало термодинамики есть один из фундаментальных законов природы вместе с первым началом - законом сохранения энергии и ее преобразования.

Это значит, что величины Q₁ и Q₂ на самом деле но произвольны, а чем-то определяются. Чтобы в этом разобраться, надо строго рассчитать, что происходит в цикле Карно. Сам Карно этого делать еще не умел, а потому он не мог прийти к важному выводу, что отношение Q₁/Q₂ равно отношению температур T₁/T₂. Повторим, что если машины не идеальные, если их работа не обратима, то это только ухудшает положение, так как возникают дополнительные потери.

Таким образом, Карно установил, что существует теоретический предел работы, которую может совершить тепловая машина. Карно не мог вывести формулу для величины этой работы, поэтому его труд остался незавершенным.

Закончим рассказ о Карно словами, которыми он сформулировал свой закон: "Движущая сила тепла не зависит от агентов, взятых для ее развития; ее количество определяется исключительно температурами тел, между которыми в конечном счете производится перенос теплорода".