Идеальный цикл Карно

Ответ на поставленный вопрос требовал уточнения многих понятий. Прежде всего надо было понять, что одно нагретое тело само по себе не может произвести работу. Для того чтобы построить тепловой двигатель, необходимо иметь, кроме нагретого тела (нагревателя), еще и второе тело, с температурой более низкой (холодильник).

В обычной паровой машине нагреватель - это котел, в котором вода превращается в пар, а холодильник - конденсатор, в котором пар, совершив работу, конденсируется, превращаясь снова в воду. Кроме нагревателя и холодильника должно существовать некоторое рабочее тело - жидкость или газ, которое переносит тепло и "по дороге" совершает работу.

Карно объясняет возникновение работы перетеканием теплорода от нагревателя к холодильнику. Поток теплорода можно сравнить с потоком воды, текущим через плотину и вращающим колесо турбины электростанции. Количество теплорода сохраняется (так же, как и количество воды), изменяется только "уровень" теплорода, который задается температурой. Итак, теплород течет от нагревателя к холодильнику и совершает при этом работу. Если, однако, продолжать аналогию между теплородом и водой, то мы быстро зайдем в тупик. Следуя этой аналогии, естественно было бы считать, что работа, которая совершается при "падении" теплорода, пропорциональна разности температур (разности "высот"). Такой вывод нас не может устроить. Действительно, если бы это было так, паровая машина была бы бессмысленна. После того как пар расширился, совершил работу и сконденсировался (или просто охладился), нам надо его опять нагреть и заставить работать еще раз. На нагревание пришлось бы затратить ровно столько работы, сколько мы получили при охлаждении,- и то только в том случае, если все наши устройства работают без потерь.

Представим себе, что кому-то пришло в голову построить гидроэлектростанцию на берегу горного озера, спуская воду через турбину в какой-то резервуар, например в другое озеро, расположенное на меньшей высоте. Чтобы избежать понижения уровня верхнего озера, будем перекачивать воду обратно с помощью насосов. Очевидно, что такая идея нелепа: работа, совершаемая насосами, будет никак не меньше работы, которую смогут совершать турбины. На самом деле часть работы будет даже потеряна на трение в турбине, на испарение воды и по разным другим причинам. Как бы мы ни устраивали насосы, включали бы их последовательно или параллельно, закон сохранения энергии не дал бы реализовать никакого полезного устройства, которое позволило бы получить выгоду из такого мероприятия.

Почему же в случае тепловой машины сжатие и расширение газа приводит к совершению полезной работы? В чем состоит разница между работой гидростанции и работой тепловой машины?

Размышления по этому поводу приводят нас к вопросу, который уже был поставлен, а именно: равноценны ли градусы на разных участках шкалы термометра? Для воды, падающей в горной речке с высоты одного метра, безразлично, где этот метр находится, в долине или высоко в горах, - работа, которую можно получить от падения одного литра воды, будет одна и та же. Этот очевидный результат можно сформулировать и иначе. Можно сказать, что, измеряя энергию, выделяемую при падении воды, мы измеряем лишь разность ее уровней, но нельзя измерить высоту места, где это происходит.

Совсем иначе обстоит дело с нагреваемым паром, и это первое, что заметил Карно. Работа, которую может произвести пар, охлаждающийся от 100 до 99 °С, не будет равна работе, которую совершит то же количество пара, охлаждаясь от 50 до 49 °С. Причина состоит в том, что давление пара будет в этих случаях разное.

Однако кроме нагревателя и холодильника существует еще и рабочее тело - может быть, от его свойств тоже что-то зависит? Карно столкнулся с тем, что в задаче участвует слишком много переменных.

Он нашел блестящий выход, рассмотрев "круговой" процесс - цикл, в котором рабочее тело сначала совершает работу, а потом возвращается в исходное состояние (используя для этого часть совершенной работы). Таким образом, в начале и в конце цикла все части тепловой машины (в том числе и рабочее тело) находятся в одном и том же состоянии, и поэтому после каждого отдельного цикла можно "подбить итог", так как следующий цикл будет во всем тождествен предыдущему.

Конструируя такой цикл, Карно рассматривал некоторую идеальную машину, о которой надо знать лишь то, что в ней есть устройство типа цилиндра с поршнем (или типа турбины), приводимое в движение расширяющимся рабочим телом, например газом. Температура газа может изменяться: его можно нагревать с помощью какой-то системы (нагревателя) и охлаждать с помощью другой системы (холодильника), Кроме того, естественно пред-положить (в этом и состоит "идеальность" машины), что ни тепло, ни работа не пропадают: тепло не излучается наружу, а работа не тратится на преодоление трения.

Для того чтобы описать, что происходит с газом, надо знать, как изменяются его характеристики: объем V, давление р, температура Т. Если температура газа не изменяется, то такой процесс называют изотермическим. Если же изменяется давление, то процесс называют изобарным. Если же не изменяется объем, то процесс изохорный. Ясно, что можно придумать сколько угодно процессов, при которых изменяются все три величины: р, V, Т. В цикле Карно как раз и используется процесс такого типа - так называемый адиабатический процесс. В адиабатическом процессе газ не получает тепла извне и не отдает его никуда; при этом ни одна из величин р, V, Т но остается постоянной.

Изменение состояния газа в круговом процессе мы будем иллюстрировать графиком, на котором по осям отложены давление и объем газа. Так как мы будем иметь дело только с идеальным газом, то такой график можно нарисовать, зная законы Бойля - Мариотта и Гей-Люссака. Будем считать, что эти законы хорошо известны и даже известно, как они объединяются в универсальное уравнение Менделеева - Клапейрона для одного моля:

где T=t+273,15 - температура по шкале Кельвина (t - температура по шкале Цельсиця), R - газовая постоянная.

Напомним еще, что отрезки кривых на графиках называют изотермой (T=const), изобарой (p=const) или изохорой (V=const). Отрезок кривой, описывающий адиабатический процесс, называют адиабатой.

Чтобы описать цикл Карно, используем мысленный опыт.

Снабдим цилиндр с газом поршнем и будем переносить его с места на место. Для простоты рассуждений не будем обращать внимания на атмосферное давление, считая, что оно мало по сравнению с давлением газа под поршнем, или, наконец, считая, что все происходит в вакууме. В таких условиях, если поршень оставить свободным, газ под ним будет расширяться.

Пусть газ вначале имел температуру T₁. Организуем следующий процесс, состоящий из четырех этапов.

I. Погрузим цилиндр в кипящую воду (это будет означать, что процесс изотермический) и дадим возможность газу расширяться. Подождем, пока он произведет некоторую работу, величину которой обозначим через А₁. Так как в данном случае работа совершается при постоянной температуре, то на графике этот этап изобразится изотермой аб (рис. 6).

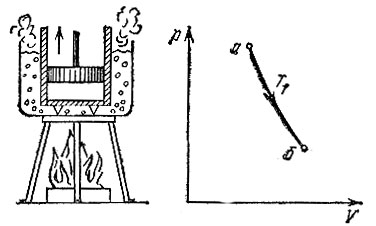
Рис. 6. Цикл Карно: I этап

При расширении газ будет забирать тепло от нагревателя. Обозначим тепло, полученное газом, через Q₁

II. Перенесем сосуд в термос и позволим газу продолжать расширяться и совершать еще работу А^'₁ Так как в термосе газу неоткуда получать тепло, то, совершая работу, газ охлаждается. Дадим ему охладиться до температуры Т₂. На графике этот процесс изобразится в виде кривой - адиабаты бв, более крутой, чем изотерма аб (рис. 7). На рисунке вместо термоса нарисован просто столик, на котором цилиндр не нагревается и не охлаждается.

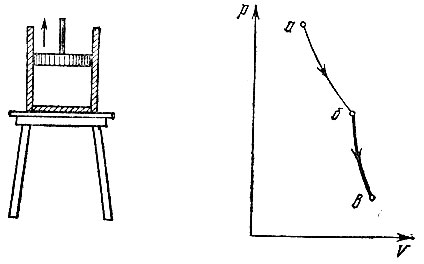
Рис. 7. Цикл Карно: II этап

III. Теперь, когда температура газа сравнялась с температурой холодильника, мы переставим сосуд в холодильник и начнем сжимать газ, следя за тем, чтобы его температура была все время постоянна и равна Т₂. На это мы затратим работу А₂, отдав холодильнику тепло Q₂. Остановим сжатие, когда давление и объем газа будут отвечать третьей вершине криволинейного четырехугольника (рис. 8). Как выбирается эта точка, мы увидим на этапе IV.

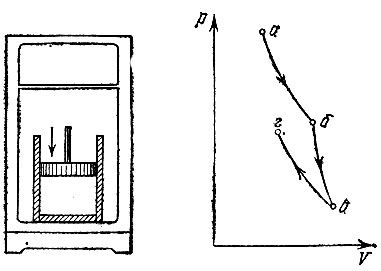
Рис. 8. Цикл Карно: III этап

IV. Перенесем теперь обратно сосуд в термос и, продолжая сжимать газ, будем следить, чтобы он вернулся в исходное состояние, т. е. чтобы его давление и температура приобрели те значения, какие они имели в начале этапа I (рис. 9). Для этого, конечно, надо правильно выбрать величины давления и объема в конце этапа III, иначе можно не попасть в исходную точку. Зная законы идеального газа, эти величины нетрудно вычислить заранее. На этапе га также придется затратить некоторую работу А^'₁.

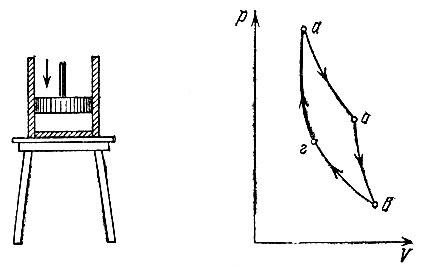
Рис. 9. Цикл Карно: IV этап

В результате после четырех этапов рабочее тело не изменило своего состояния, нагреватель потерял количество теплоты Q¹, а холодильник получил тепло Q₂. Количество теплоты Q₁ - Q₂ ушло на совершение работы.

Смысл всего рассказанного пока сводится к тому, что тепловая машина не может использовать все тепло, полученное от нагревателя, часть тепла должна быть отдана холодильнику.

Это заключение, конечно, не слишком неожиданное, хотя для того времени и не столь очевидное. Более существенно другое. Карно доказал, что описанный процесс является оптимальным и что при этом доля использования тепла 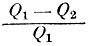зависит только от температур T₁ и T₂ и не зависит ни от каких других факторов, в частности, от свойств рабочего тела.

Это утверждение казалось противоречащим здравому смыслу, естественно было считать, что изменением характера процесса или свойств рабочего тела можно регулировать эффективность работы машины.

Теорема Карно и ее доказательство относятся к числу самых красивых построений в физике. С этой теоремы учение о тепле присоединялось к числу точных наук, к которым, как мы говорили, относились механика и оптика.

В открытии Карно удивительно то, что он не использовал закона сохранения энергии, когда писал свой мемуар. Перенос тепла для него был "падением" теплорода. Однако пользуясь опытными данными об измерении теплоемкости газа при изменении его плотности, Карно пришел к заключению, что "падение теплорода производит больше движущей силы при низких градусах, чем при более высоких". Движущей силой Карно называл работу, производимую машиной за один цикл. Отсюда и название его мемуара.