
Закон сохранения энергии
Теплород должен сохраняться; работа производится за счет "падения" теплорода с высокого уровня на более низкий. Температура в такой теории играла роль потенциальной энергии, и если бы физики лучше понимали механику, то их должно было бы обеспокоить, что у теплорода нет ничего похожего на кинетическую энергию.
Положение с теплом запутывалось еще и из-за того, что физики не очень хорошо понимали, что такое энергия. Сам термин "энергия" появился лишь в начало XIX века; он был введен в механику Юнгом. Поэтому, может быть, не следует удивляться, что превращения энергии и ее сохранение были открыты не физиком, а врачом Робертом Майером.
В 1840 г. Майер в качестве корабельного врача отправился на остров Ява. В дневнике, который он вел весьма аккуратно, сохранились две записи. В одной он записал свой разговор со штурманом, который рассказал ему, что во время бури вода в океане нагревается. Может быть, это и был первый шаг к открытию. Вторая запись относится к тому, что он заметил, когда пускал кровь (как это было принято в медицине в те годы) матросам, заболевшим воспалением легких. Майер обратил внимание на то, что местные врачи знали давно и не удивлялись этому. Венозная кровь у матросов не была темной, как это привык видеть европейский врач, кровь была ярко-красной. Майер придумал этому неожиданное объяснение. Человек похож на тепловую машину. Тепло, которое выделяется в его теле, возникает в результате сгорания пищевых продуктов. Животное тепло, о котором говорили и писали ученые, по сути дела, ничем не отличается от любого другого тепла: его производство требует топлива. Сгоревшие остатки - углекислый газ - кровь "отвозит" обратно в легкие. Кровь, наполняясь "дымом", сгоревшими продуктами, темнеет. В жарком климате тепла требуется мало, топлива расходуется меньше, сгорание происходит не столь интенсивно и кровь почти не темнеет.
Главным в этой картине было предположение, что тепло выделяется за счет энергии химической реакции. Мысль, на наш взгляд, простая, но весьма неожиданная для ученых того времени. Даже замечание Майера о том, почему нагревается вода во время бури, не было принято учеными профессорами в Тюбингене, куда он обратился за поддержкой.
Статья, которую он отправил в июле 1841 г. в журнал Поггендорфа (о нем мы уже упоминали), была не замечена редактором. Майер даже не получил простого извещения от редакции. Работа была, правда, написана туманно - писал ее врач, физикой не занимавшийся. Статья носила название "О количественном и качественном определении силы. Сочинение Ю. Р. Майера, доктора медицины и хирургии, практического врача в Гейльбронне".
Через год Майер публикует в химическом журнале новую работу, уже подкрепленную вычислениями. На этот раз ему помог знаменитый химик Либих.
Но только в 1845 г. Майеру удалось опубликовать подробный труд "Органическое движение в его связи с обменом веществ" (название, как мы видим, тоже не очень привлекательное для физиков).
За это время Майер не только понял, что энергия превращается из одного вида в другой, но и нашел, опираясь на опыты Гей-Люссака, механический эквивалент тепла -365 кгc*м/ккал.
Для биологов выводы Майера также были странными. Многие биологи (их называли виталистами) считали источником деятельности живого организма некую специфическую жизненную силу. Современное понимание глубокой связи биологии и физики имеет свое начало в открытии Майера. Судьба Майера была тяжелой. Его травили ученые коллеги, его не понимали близкие. Десять лет он провел в психиатрической больнице. Лишь в последние несколько лет перед смертью (1878 г.) он получил признание.
В те же годы, когда Майер тщетно пытался убедить ученый мир в правильности своих идей о превращении энергии в тепло, в Англии похожие мысли развивал Джоуль.
Первая работа Джоуля относится к 1841 г. Она была посвящена исследованию выделения тепла в проводниках с током. Интересно, что в том же году Майер впервые вычислил тепловой эквивалент работы, сообщив о нем в письме к своему другу Бауру. Однако он опубликовал свои результаты позже.
Джоуль заключил из опытов, что тепло выделяется за счет работы батареи в результате происходящих в ней реакций. Отсюда Джоуль пришел к открытию закона, который сейчас называют законом Джоуля - Ленца.
Свою уверенность в природе тепла Джоуль подкрепил опытами и так же, как и Майер, определил механический эквивалент тепла. Такие опыты Джоуль производил в течение многих лет. Все опыты доказали, что тепло возникает в результате совершения работы. Тем самым было, наконец, показано, что теория не уничтожаемого теплорода неверна и должна быть забыта.
Джоуль тоже далеко не сразу завоевал признание современников. Слишком велико было влияние старых теорий, державшихся на вере в авторитеты, чтобы принять новые представления об эквивалентности тепла и работы.
Но все новые и новые опыты подтверждали эти идеи в самых разных условиях. Либих не забыл того, что он узнал от Майера, и в работе "О животном тепле" решительно защищал вывод о том, что все тепло, возникающее в живом организме, получается за счет сгорания пищи.
В 1847 г. идеи "о сохранении силы" (т. е. энергии) получили свое развитие в работах Гельмгольца (не оценившего в свое время заслуг Майера).
Так в 40-х годах XIX века в результате работ многих естествоиспытателей был сформулирован, наверное, самый "главный" закон природы - закон сохранения энергии, который применительно к тепловым процессам называют еще и первым началом термодинамики.
Интересно, что на пути признания этого закона встретилась еще одна трудность. В утверждение, что энергия не возникает из ничего, что нельзя построить вечный двигатель, можно было, в конце концов, поверить. Трудно было понять, что энергия не может исчезать. Работа лошади тратится на трение в колесах телеги, тепло нагретой печки рассеивается безвозвратно по комнате. На каждом шагу мы видим, как исчезает энергия, как работа тратится впустую, и тем не менее говорим, что энергия сохраняется. Разрешен парадокс был лишь тогда, когда поняли, что тепло связано с движением молекул и что "исчезнувшая энергия" переходит в энергию этого движения.
Настало время вернуться к Карно. Ни Майер, ни Джоуль о нем не вспоминали. Объяснение закона сохранения энергии и принципа Карно было завершено Клаузиусом. Его работа была опубликована в 1850 г. Поггендорфом в журнале, в котором не нашлось места работе Майера. Клаузиус первый заговорил об эквивалентности тепла и работы как о первом начале теории тепла и написал уравнение, которого не хватало Карно. Для этого надо было прежде всего сформулировать простое утверждение: всякое тело имеет внутреннюю энергию, которую можно увеличить двумя путями -производя над телом работу и подводя к телу тепло. Смысл этого утверждения заключен в союзе "и". Сказанное можно записать в виде формулы:
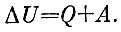
В этой простой формуле заключен глубокий смысл. В механике энергия тела увеличивается, когда какие-либо внешние силы производят над этим телом работу. Это утверждение можно записать так:
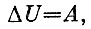
понимая, например, под А работу сжатия пружины, а под ΔU - увеличение ее потенциальной энергии. Но энергию пружины можно увеличить не только сжатием. Она увеличивается и при нагревании. Подводя к какой-либо системе тепло, мы также увеличиваем ее энергию.
Очень важно понимать, что по конечному состоянию системы нельзя никаким образом обнаружить, за счет чего система увеличила свою энергию: за счет тепла или за счет работы. Сам Клаузиус называл U "теплом, содержащимся в теле", противопоставляя ему Q - "тепло, сообщенное телу". Сейчас U называют внутренней энергией (или просто энергией) тела, ΔU есть ее приращение.
Как мы сказали, энергию тела U можно изменить как подводя тепло, так и совершая работу, но эти вклады, так сказать, обезличиваются, превратившись в единую физическую величину - энергию U*. Не существует величины, которую можно было бы назвать теплотой тела Q, как нет внутри тела величины, которую можно назвать работой А. К состоянию с одной и той же энергией U можно прийти разными способами, по-разному выбирая количество сообщаемой теплоты и работы, оставляя одной и той же лишь их сумму. В этом и заключалась главная "хитрость" природы, путь к пониманию которой оказался столь трудным и долгим.
* (Клаузиус утвердил в науке о тепле понятие энергии (точнее, внутренней энергии). Он взял это слово из механики: "Что касается... названий, то особенно подходящим мне представляется употребленное Томсоном слово "энергия", ибо величина, о которой здесь идет речь, вполне соответствует величине, обозначаемой этим именем в математике...". Другие физики предлагали названия "внутренняя теплота", "внутренняя работа", "функция действия".)
Теперь мы можем закончить рассказ о цикле Карно и получить формулу для коэффициента полезного действия тепловой машины. Однако чтобы сделать это, нам надо знать формулу для работы газа (формулы для идеального газа нам будет достаточно, так как цикл Карно можно рассчитать для какого-либо одного тела).
Работа, которую надо затратить, чтобы сжать 1 моль идеального газа от объема V0 до объема V при постоянной температуре, равна
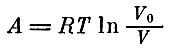
(ln - натуральный логарифм. Если 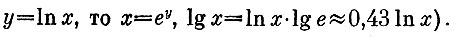
Если V0<V (газ расширяется), то А<0 - работа совершается газом.
Формула эта выводится так.
Состояние идеального газа, как мы знаем, удовлетворяет уравнению состояния Менделеева - Клапейрона*
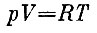
(мы будем считать, что у нас есть ровно один моль газа).
* (Клаузиус утвердил в науке о тепле понятие энергии (точнее, внутренней энергии). Он взял это слово из механики: "Что касается... названий, то особенно подходящим мне представляется употребленное Томсоном слово "энергия", ибо величина, о которой здесь идет речь, вполне соответствует величине, обозначаемой этим именем в математике...". Другие физики предлагали названия "внутренняя теплота", "внутренняя работа", "функция действия".)
Пусть газ находится в сосуде с поршнем. Приложим к поршню давление р. Поршень будет сжимать газ, производя работу. Если площадь поршня равна а, то на поршень действует сила рσ. Если эта сила остается постоянной, то, сдвинув поршень на длину Δl, сила произведет работу ΔА=рσМ. Нетрудно видеть, что произведение σ Δl есть не что иное, как уменьшение объема газа,-ΔV" Итак, выражение для работы, совершенной над газом имеет вид (рис. 11)
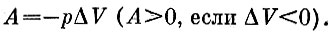
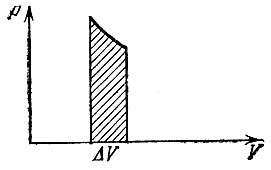
Рис. 11 Изотермическое сжатие газа
С помощью уравнения идеального газа исключим давление:
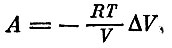
или
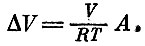
Это и есть уравнение, которое нам надо решить. Те читатели, кто знаком с производными, знают, что это просто дифференциальное уравнение
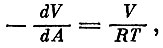
решение которого
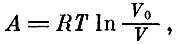
где V0=const.
Повторим этот вывод более подробно.
Пусть газ сжимается от объема V до объема, например,1/2V (т. е. ΔV=1/2V). Повторим эту операцию 10 раз. В конце этапов объем принимает значения1/2V, 1/4V,1/8V, ...,1/210V. Посмотрев на только что написанное уравнение, мы увидим, что для того чтобы объем уменьшился от значения V до V, надо совершить работу, примерно равную
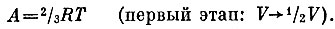
Вместо того чтобы точно учитывать изменения объема в правой части, мы заменили V на полусумму 1/2(V+1/2V)=3/4V значений объема в начале и в конце этапа. Ясно, что, сужая этапы, уменьшая изменение объема, можно сделать ошибку этого приближения сколько угодно малой.
Вычислим таким же образом работу, совершаемую над газом па втором этапе. При этом мы опять заменим объем на полусумму (1/2V+1/4V)=3/8V, Чтобы снова уменьшить объем вдвое, надо положить ΔV=1/4V, откуда получаем
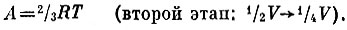
Дальше уже нетрудно увидеть, что на любом этапе при уменьшении объема в два раза совершается одна и та же работа:
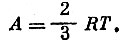
Таким образом, затраченная работа будет расти в арифметической прогрессии, в то время как объем будет уменьшаться в прогрессии геометрической.
Мы можем теперь написать такие же формулы для случая, когда начальный объем V0 уменьшается на каждом этапе лишь на очень маленькую часть 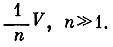
В этом случае после N этапов (N>>1)отношение объемов будет равно
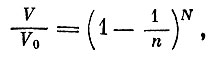
а совершенная работа
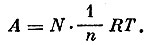
Исключая из этих формул N, получаем связь между изменением объема 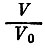 и работой А:
и работой А:
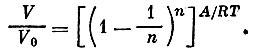
Если теперь устремить то выражение в квадратных скобках будет стремиться, как известно, к 1/е=1/2,7182...:
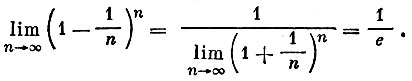
Таким образом,
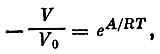
или
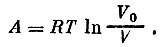
Полезно привести геометрическую иллюстрацию полученной формулы. Нарисуем график (рис. 12) функции p(V, Т) при постоянной Т, т. е. гиперболу
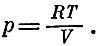
Работа А при изменении объема V на ΔV есть площадь заштрихованной полоски, а вся работа на сжатие газа от объема V0 до объема V равна, очевидно, площади фигуры под отрезком гиперболы, обведенной двойной линией.
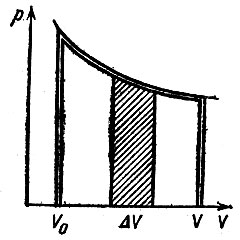
Рис. 12 Работа при изотермическом сжатии
|
ПОИСК:
|