Распределение энергии по степеням свободы

Мы уже знаем, что на каждую степень свободы в одноатомном газе приходится энергия 1/2kT. В СИ можно было бы выбрать за градус температурной шкалы такую величину, при которой энергия, приходящаяся на одну степень свободы, изменяется на 1/2 джоуля. В такой системе единиц одно деление шкалы термометра соответствовало бы 0,7 * 10²³ К и в формуле для энергии исчезла бы постоянная Больцмана. Эта величина, конечно, слишком велика для практических целей, поэтому градусы Кельвина (или Цельсия) продолжают господствовать в физике. Мы узнаем впоследствии, что в ядерной физике и особенно в астрофизике энергетическая температурная шкала становится удобной. Более практичная шкала получилась бы, если изменению температуры в один градус отвечало бы изменение энергии одной степени свободы атома, но рассчитанное не на один атом, а на N_A атомов, т. е. на 1/2R. О такой шкале мы уже говорили и обозначили градус в этой шкале через θ Тогда энергия 1 моля одноатомного газа записывалась бы в виде 3/2θ Но такую шкалу никто не вводил.

Если газ не одноатомный, то часть энергии уходит на колебания атомов внутри молекул и на вращение самих молекул. Пусть, например, речь идет о двухатомной молекуле типа О_{" атома кислорода, не объединенные в молекулу, характеризуются шестью степенями свободы. Число степеней свободы не изменится, когда атомы объединяются в молекулу O2. У такой молекулы есть три поступательные степени свободы и две вращательные - молекула может вращаться вокруг двух осей (рис. 14).}

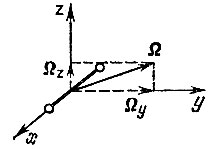
Рис. 14. Вращение двухатомной молекулы

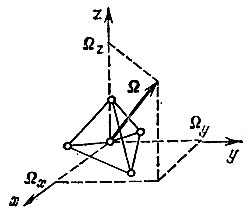
Рис. 15. Вращение многоатомной молекулы

По не очень понятной в классической физике причине молекула не вращается вокруг своей оси - точнее, с этой степенью свободы не связана какая-либо энергия. Можно это объяснить тем, что атомы точечные и их нельзя раскрутить. Ситуация становится ясной лишь в квантовой механике. Если молекула состоит из трех или большего числа атомов, не расположенных на одной прямой, то вращение может происходить вокруг любого направления - говорят, что молекула в этом случае имеет три вращательные степени свободы (рис. 15).

Остается еще шестая степень свободы -это колебания атомов друг относительно друга. Эти колебания нас и интересуют.

В то время как поступательное движение и (как это можно доказать) вращения получают по 1/2kТ энергии, колебания получают целое kТ. Понять это можно, заметив, что молекула, как упругая пружинка, имеет, кроме кинетической энергии, еще и потенциальную, которая забирает ровно половину всей энергии молекулы. Это нетрудно доказать и строго, рассмотрев движение упругой пружинки.

Таким образом, молекула O₂ имеет энергию

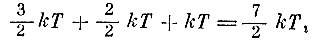
т. е. теплоемкость кислорода при постоянном объеме равна 7/2k на молекулу, или 7/2R на 1 моль.

По-другому обстоит дело в кристалле. В твердых телах частицы не могут свободно перемещаться в пространстве и в не слишком сложных по строению веществах не вращаются. Поэтому практически все степени свободы относятся к колебаниям. Это значит, что теплоемкость моля равна 3R кал/К - по R на каждое колебание (каждый атом может колебаться в трех направлениях). Так как R примерно равно 2 кал/(моль*К), то теплоемкость всех веществ в твердом состоянии должна была бы равняться 6, что и составляет содержание закона Дюлонга и Пти. Опыт показывает, однако, что не для всех твердых тел теплоемкость равна 6, кроме того, она зависит от температуры. Особенно яркое "несогласие" с законом Дюлонга и Пти было обнаружено у углерода.

Этот вывод казался в прошлом веке очень странным, так как он противоречил закону равнораспределения. Следствия отклонений от закона Дюлонга и Пти оказались, однако, более серьезными, чем можно было ожидать. Они предвещали катастрофу классической физики, разразившуюся в конце века. О ней будет рассказано дальше,