Распределение Максвелла

Все, что было сказано выше, есть следствие того факта, что газ, предоставленный самому себе и находящийся в постоянных внешних условиях (например, газ, заключенный в сосуд, стенки которого находятся при постоянной температуре), приходит в состояние равновесия.

С макроскопической точки зрения в нем устанавливаются постоянная температура, постоянное давление, а если газ состоит из нескольких компонент (как воздух), то и состав газа в разных местах в сосуде будет одинаков.

Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Однако не все изменяется столь хаотически. Как бы ни изменялась скорость, среднее значение ее квадрата остается постоянным. Это значит, что, если бы мы могли следить за какой-нибудь молекулой достаточно долго, мы увидели бы, что она будет то ускоряться, то замедляться, хотя в среднем квадрат ее скорости будет постоянным (средним по времени), Тот же результат получится, если мы вместо того, чтобы следить за одной молекулой, измерили бы в какой- то момент времени скорости множества разных молекул: среднее значение опять оказалось бы тем же (средним по числу молекул)^*.

^* ( Внимательный читатель может спросить, почему при двух способах определения средней скорости результат будет одним и тем же. Среднее по времени ввел в физику Эйнштейн, и то, что среднее по времени равно среднему по числу молекул, до сих пор не доказано до конца.)

Зададим вопрос: сколько молекул, т. е. какая их часть, движется с определенной скоростью в данный момент? Эту задачу решил Максвелл (общая теория статистических свойств физических систем была развита Больцманом и Гиббсом),

Мы не будем выводить формулу распределения Максвелла. Для наших целей важно только то, что согласно этой формуле распределение молекул по скоростям определяется множителем, имеющим вид экспоненты, т. е.

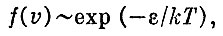
где ε =mv²/2 - кинетическая энергия молекулы.

Максвелл опубликовал свою формулу в 1859 г. Его вывод казался очень странным. Он не решал подробно уравнений для каждого из сталкивающихся атомов, а сразу получил условия для равновесного состояния системы из большого числа атомов. Но такие условия никак не следовали из механики. Не удивительно, что даже Томсон пытался проверять закон распределения, рассматривая механику бильярдных шаров^*. Максвелл возвращался вновь к выводу своей формулы в 1867 г. В новой работе он доказал, что полученное им распре-деление действительно не изменяется при соударениях молекул. Строгий вывод распределения Максвелла на самом деле оказался нелегким делом, в котором еще до сего времени не все прояснилось.

^* (Бильярд оказался популярной моделью для исследования поведения коллектива атомов. Теория сталкивающихся шаров на бильярдных столах разной формы развилась в интересную область математики.)