Что такое распределение?

На первый взгляд, во фразе: "Столько-то молекул в газе имеет скорость, например, 200 м/с" - нет ничего странного. Но это число 200 не может быть совершенно точным. Точных значений бесконечно много, а молекул хотя и много, но все-таки конечное число. Поэтому в каждый данный момент молекулы не могут иметь все возможные скорости. Но это и не нужно. Всякую скорость мы измеряем с какой-то точностью, а поэтому на самом деле речь идет не точно о скорости 200 м/с, а о неком интервале скоростей от 200-6 до 200+6, где 6 - некоторая малая величина, отвечающая условиям опыта.

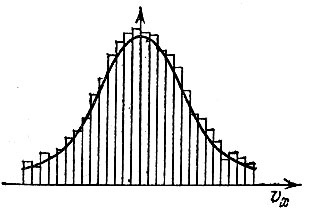
Рис. 16 Гистограмма и кривая распределения (для v_x)

Если говорить не об абсолютной величине скорости, а, скажем, о компоненте v_x, то можно задать вопрос: сколько молекул (или, лучше, какая доля молекул) имеют компоненту скорости, лежащую в интервале от v_x до v_x+Δv_x? Такую величину можно записать в виде Δn(v_x)=f(v_x)Δv_x. Функцию f(v_x) называют функцией распределения.

На рис. 16 изображены две диаграммы. Ступенчатая линия описывает примерное распределение молекул, так что площадь каждого (п-гo) прямоугольника (она равна f_nΔv_x) есть доля молекул, имеющих скорости, лежащие в соответствующем интервале. Величина интервала Δv_x выбрана равной единице. Такая диаграмма называется гистограммой. Если число ступенек гистограммы очень велико, то ступенчатую линию можно заменить гладкой (она также изображена на рисунке). Эта линия и есть функция распределения. Так как f(v_x) определяет долю молекул, то площадь под всей кривой должна быть равна единице.

Точно такие же графики - гистограммы - можно построить для функций распределения двух других компонент: v_y и v_z.

Теперь напишем выражение для доли молекул, которые имеют компоненты скоростей v_x, v_y и v_z (также в некоторых интервалах вокруг этих значений) . Это можно сделать так. Доля молекул, имеющих компоненту скорости v_x, равна f(v_x)Δv_x. Из этих молекул некоторая часть имеет вторую компоненту, равную v_y. Доля таких молекул, очевидно, равна

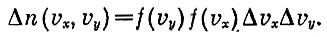
Из числа этих молекул доля f(v_z) будет иметь третью компоненту скорости v_z. Значит, доля всех молекул, имеющих скорость с компонентами v_x,v_y, v_z будет равна

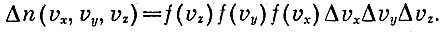
Функцию

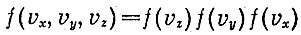
можно назвать функцией распределения молекул по скоростям. Все три функции распределения по компонентам скоростей взяты одинаковыми, так как в тепловом равновесии все три направления в пространстве ничем не отличаются друг от друга.