Разные средние

Если принять, что закон распределения молекул по скоростям известен, то можно вычислить и разные характеристики этого распределения. Для среднего квадрата скорости получается уже известная нам формула:

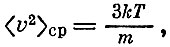
или для средней кинетической энергии:

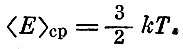
Можно найти и среднее значение абсолютной величины скорости^*:

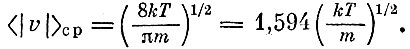
^* (Среднее значение компоненты скорости равно нулю, так как отрицательные и положительные значения компонент равноправны. Вычисление средних сводится к вычислению интегралов и элементарно сделано быть не может.)

Наконец, "наиболее часто" встречаются молекулы со скоростью (наиболее вероятная скорость)

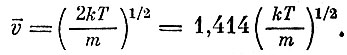
Не следует удивляться, что молекулы со средней скоростью встречаются не очень часто. Абсолютная величина скорости - величина положительная, и число молекул, имеющих скорость меньше средней, всегда больше, чем число молекул, имеющих скорость больше средней '(чтобы "уравновесить" молекулы с большими скоростями, надо иметь большее количество молекул с маленькими скоростями)^*.

^* ( Это хорошо известно статистикам. Число людей, получающих зарплату больше средней, всегда меньше, чем число людей, получающих зарплату меньше средней. )

Если бы все молекулы имели одинаковую скорость, то все три величины были бы, конечно, равны друг другу. Их различие показывает, насколько разбросаны значения скоростей.

Для того чтобы характеризовать разброс скоростей, оказывается удобным вычислить еще средний квадрат кинетической энергии

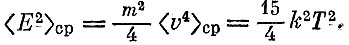
Составим теперь разность, которая называется дисперсией:

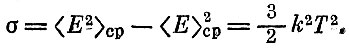
Мы обнаруживаем, что температура выступает еще в одном качестве: она характеризует "ширину", разброс распределения молекул по скоростям (или энергиям), т. е. величину естественного разброса кинетической энергии молекулы вокруг среднего ее значения.