Распределение Максвелла и хаос

Остановимся еще немного на распределении Максвелла. Прежде всего, описывая газ, перейдем, как говорят, из пространства координат в пространство скоростей. Это значит, что мы будем "изображать" каждую молекулу точкой с координатами, равными компонентам скоростей этой молекулы. Так, точка в начале координат соответствует покоящейся молекуле, точки на оси х - молекулам, движущимся с разными скоростями вдоль оси х, и т. д. Такое пространство изображено на рис. 17.

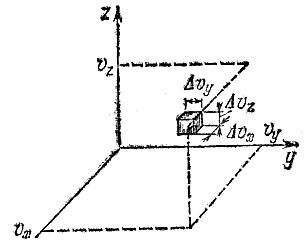
Рис. 17 Элементарный кубик в пространстве скоростей

Представим себе кубик с одной из вершин в точке (х, y, z) и с ребрами, параллельными осям координат. Внутри этого кубика будут находиться точки, соответствующие молекулам, компоненты скоростей которых лежат в интервалах, определяемых координатами вершин кубика. Число таких молекул на самом деле все время меняется - молекулы сталкиваются друг с другом, изменяют свои скорости. Эти процессы будут приводить к тому, что точки в кубике будут то появляться, то исчезать. Если точка исчезла, значит, где-то в другом кубике (мы легко можем себе представить, что все "пространство скоростей" разбито на такие кубики) появится новая точка.

Ясно, что общее число точек, которое равно полному числу молекул в газе, остается постоянным. Если бы нас попросили подробно описать, что происходит в каком-нибудь кубике, то это была бы непосильная задача.

Однако нас не интересуют такие подробности, они нам просто ни к чему - все равно мы не знали бы, что с ними делать. На самом-то деле нас интересует, сколько молекул находится в этом кубике в среднем, и на этот вопрос дает ответ распределение Максвелла.

Нетрудно понять, что функция распределения может зависеть только от квадратов скоростей, ибо она не должна зависеть, очевидно, от их направлений. Если бы это было не так, то в каком-то направлении летело бы больше молекул, чем в другом, и весь газ двигался бы как целое.

Но мы знаем, что эта функция должна распадаться на три одинаковых множителя, каждый из которых зависит только от одной компоненты скорости (точнее, от ее квадрата).

Квадрат скорости равен сумме квадратов компонент: v=v²_x+v²_y+v²_z. Итак, задача состоит в том, чтобы найти такую функцию от v², которая распадалась бы на произведение трех одинаковых функций от v_x, v_y и v_z соответственно.

Можно показать, что единственная функция, удовлетворяющая этому условию, записывается в виде

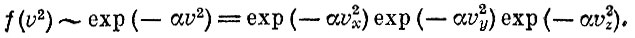
Дальнейшие расчеты требуют вычисления интегралов, мы их приводить не будем. Заметим только, что коэффициент

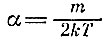
находится из условия, чтобы среднее значение, например <>v²_x>, удовлетворяло старому условию

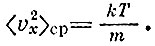
Можно еще написать функцию, которая описывает распределение молекул по кинетической энергии, т. е. определяет долю молекул, имеющих кинетическую энергию в интервале ε, ε+ Δε. Такая функция имеет вид

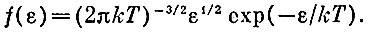
Эта функция также называется функцией распределения Максвелла.

Из того факта, что функция распределения распадается на множители, вытекает, что распределения по всем осям не зависят друг от друга и подчиняются одному и тому же закону. Можно сказать, что вероятность для молекулы попасть в некоторый выбранный нами кубик, т. е. вероятность того, что в результате столкновений молекула приобретает скорость, отвечающую координатам внутри этого кубика, распадается на три множителя - вероятности каждой из компонент скорости молекулы оказаться в интервале значений, отвечающем ребру кубика.

Такую задачу можно проиллюстрировать игрой в кости. Пусть мы бросаем три игральные кости, выкрашенные в разные цвета. Вероятность того, что на одной из костей, например красной, выпадет пятерка, равна 4/6. Такова же вероятность того, что на зеленой кости выпадет тройка (или на желтой- четверка).

Почти очевидно, что если мы будем бросать все три кости сразу, то вероятность любой комбинации, например 3 (красная)+4 (зеленая)+1 (желтая), будет равна произведению 1/6*1/6*1/6=1/256.

Основанием для такого решения служит интуитивная уверенность, что бросание каждой кости никак не зависит от бросания других, а потому все тройные комбинации чисел от 1, 1, 1 до 6, 6, 6 должны выпадать одинаково часто, т. е. иметь одинаковую вероятность. Процесс распределения молекул по скоростям в результате столкновений, конечно, не похож на бросание костей. Этот процесс только демонстрирует, почему произошел распад на три множителя.

Вывод распределения Максвелла хотя и не очень прост, но кажется настолько логичным, что никакого другого распределения вроде бы и быть не может.

Чтобы подчеркнуть, насколько ошибочными могут оказаться "очевидные" вещи, следует сказать, что распределение Максвелла не описывает газ, в котором существенную роль играют квантовые свойства (например, электроны в металле или газ, состоящий из фотонов). Для таких систем функция распределения выводится из совсем других предположений.

Газ, в котором молекулы распределены по Максвеллу, обладает замечательным свойством. Такое распределение не изменяется со временем. Каждая отдельная молекула изменяет свою скорость очень часто (сталкиваясь с другими молекулами). Но на место молекулы, выбывшей из кубика, приходит другая молекула. Если мы не различаем молекулы между собой (а это, конечно, так!), то распределение молекул будет оставаться все время одним и тем же.

Если наполнить какой-либо сосуд газом, то через некоторое время распределение его молекул по скоростям станет равновесным, максвелловским. Это должно произойти совершенно независимо от того, какое распределение газ имел в начальный момент - молекулы его могли иметь, например, одинаковые скорости или двигаться еще как-нибудь, но после некоторого времени должно установиться равновесное распределение.

Если немножко подумать, то это утверждение должно показаться странным и даже не вполне правдоподобным. В задачах механики мы привыкли к тому, что надо задать начальные координаты и скорости, чтобы определить с помощью уравнений Ньютона положение и скорости частиц в более поздние (или более ранние) моменты времени. При этом разные начальные данные приведут к разным состояниям системы. В механике, как говорят, система "помнит" свои начальные условия, т. е. там всегда можно, в принципе, восстановить историю системы.

В газе все происходит по-другому. Каким бы ни было распределение скоростей в нем в исходный момент времени, оно должно превратиться в одно и то же распределение Максвелла. В этом случае система "забывает" свою историю, и по распределению молекул газа в равновесии почти ничего нельзя узнать о том, в каком он был состоянии раньше.

История газа, которым мы заполнили сосуд, разбивается на два периода. В первый период молекулы сталкиваются между собой или со стенками и их распределение приближается к равновесному. Этим периодом занимается специальная наука о неравновесных системах. После нескольких сотен или тысяч соударений каждой молекулы газ практически переходит в равновесное состояние. Дальше соударения уже ничего не изменяют.

Не следует, конечно, забывать, что установление равновесия требует времени. Если столкновения редки или если при столкновениях скорость почти не изменяется, то равновесие устанавливается медленно - время "релаксации" в такой системе очень велико. Поэтому, перед тем как применять законы теплового равновесия, надо убедиться в том, что такое равновесие существует. Между воздухом в комнате и воздухом на улице теплового равновесия нет. Закутанная в одеяло кастрюля с супом остывает медленно. Мы встретим и более интересные примеры такого рода.

Если совсем не учитывать столкновений, т. е. если газ достаточно разрежен, то мы придем к модели идеального газа, в котором столкновения нужны лишь для установления равновесия^*.

^* (Если столкновений между молекулами почти нет, то равновесие, как уже говорилось, все же будет устанавливаться благодаря столкновениям со стенками.)

Столкновения молекул приводят к тому, что уравнение идеального газа отличается от уравнения Менделеева - Клапейрона.

Равновесное состояние газа, о котором мы говорим, можно описать так: в равновесном газе существует молекулярный "хаос". Слово "хаос" надо понимать в том смысле, что система не сохранила никакой информации о своем прошлом.

Понятие "хаоса" позволяет упростить обоснование некоторых формул. Например, когда выводилась формула для давления газа на стенку сосуда, мы рассуждали о том, как молекула отражается от стенки. В действительности молекула, как правило, ударившись о стенку, прилипает к ней на некоторое время, а потом, оторвавшись, летит в какую-нибудь сторону, "забыв" о том, откуда она прилетела. Поэтому бессмысленно обсуждать процесс отражения и проще рассуждать так: поскольку свойства газа не зависят от направления, то количество движения, переносимое газом в сторону стенки, должно быть равно количеству движения, которое несут молекулы газа, летящие от стенки. Этот факт не должен зависеть ни от каких подробностей взаимодействия газа со стенками, он связан только с хаотичностью движения молекул. Если бы оба потока (к стенке и от стенки) были разными, т. е. несли с собой разное количество движения, то на некотором расстоянии от стенки это можно было бы обнаружить - газ "запомнил" бы, что он отражался от стенки. Но это противоречит гипотезе, что газ "хаотичен" и ничего не "помнит".

А раз газ не "помнит" о стенке, то результат вывода не должен зависеть от свойств стенки и от того, как атомы газа отражались от нее. В частности, атомы не "помнят" о том, какую форму имеет сосуд, и формула распределения будет одинаковой для любого сосуда, о чем мы уже говорили.

Другой случай "забывчивости" газа обнаруживается, если взять сосуд с газом, разделенный перегородкой на две части. Если вынуть перегородку, то газ из обеих половинок перемешается, и ясно, что никакими способами нельзя опознать, какой атом находился в начале опыта в правой и какой в левой половинке.

Когда горячий чайник остывает, нагревая воздух в комнате, никаким способом нельзя впоследствии определить, почему нагрелся воздух. Всем ясно, что, измеряя температуры в разных точках комнаты вдали от чайника, нельзя определить форму чайника, который нагревает комнату. Это совсем не похоже на электромагнитное поле: свет, отражаясь от поверхности, переносит информацию о поверхности. Горящая лампа хорошо видна, освещенная собственным светом. Чайник можно "увидеть" с помощью прибора, регистрирующего инфракрасные волны. Но инфракрасное излучение - это направленные электромагнитные волны, которые могут нагревать детектор. Испускаемые чайником, они не находятся в тепловом равновесии с воздухом, не рассеиваются его атомами, поэтому они могут передать образ чайника, который они "запомнили". Напротив, хаотическое движение молекул не может передать такой информации.