Термодинамическая температура и квантовая механика

Начало отсчета шкалы температур лежит при -273,15 градусах по Цельсию. Эта точка называется абсолютным нулем. Ее смысл прояснился после того, как кинетическая теория газов связала давление газа с кинетической энергией его атомов. Из этой теории казалось ясным, что при абсолютном нуле прекращается всякое движение атомов и термодинамическая температура Т есть просто мера их кинетической энергии.

Но это простое и почти наглядное объяснение было неверным. Электроны в металлах движутся с большими скоростями даже при T=0. Квантовая механика заставила совсем по-иному посмотреть на движение электронов и атомов.

Но она отнюдь не усложнила картину. Напротив, многие понятия получили в квантовой механике естественное объяснение. К таким понятиям относится и понятие о термодинамической температуре и об абсолютном нуле.

Но чтобы рассказать, что происходит с температурой в квантовой механике, надо иметь хоть какое-нибудь представление об этой науке. К сожалению, рассказать об этом в нескольких словах нельзя. Но, с другой стороны, нам и нужно очень немного. Поэтому придется поступить так: сообщать без доказательства некоторые сведения из квантовой механики, только стараться использовать таких фактов как можно меньше.

Сейчас нам надо знать, как ведет себя электрон, помещенный в магнитное поле. В квантовой механике это описывается следующим образом.

Электрон можно сравнить (хотя это сравнение не совсем точно) с вращающимся волчком. Более правильно говорить, что электрон, как и вращающийся волчок, имеет угловой момент, называемый спином, и не входить в подробности о его вращении. Со спином электрона связан и магнитный момент - электрон ведет себя в магнитном поле, как магнит.

Если электрон находится в постоянном магнитном поле, то, согласно правилам квантовой механики, его спин может быть направлен либо по полю - тогда проекция спина на направление поля равна +1/2 ћ , либо против поля и его проекция равна -1/2 ћ (ћ - постоянная Планка).

Магнитный момент у электрона направлен против спина (заряд электрона -е < 0), и он может иметь поэтому, так же как и спин, две проекции на направление магнитного поля: - μ₀, если спин направлен по полю (μ₀ >0), и + μ₀, если спин направлен против поля. Величина μ₀ называется магнетоном Бора и равна

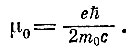
По величине магнетон Бора равен дипольному моменту двух зарядов +е и -е, расположенных на расстоянии l= 2*10^-13 м друг от друга (-е - заряд электрона, m₀ - его масса) . Численно μ₀=9,3* 10^-24 Дж/ Тл. Потенциальная энергия магнитного момента в магнитном поле В равна - μB, где μ -проекция этого магнитного момента на направление поля. Знак минус указывает, что энергия минимальна, когда μ, имеет наибольшее значение. Следовательно, потенциальная энергия электрона в поле равна либо + μ₀B, когда спин направлен по полю, либо - μ₀B когда спин направлен против поля. Все эти рассуждения сводятся к тому, что в магнитном поле электрон может находиться в одном из двух состояний, а энергия этих состояний равна ±μ₀B. При этом мы считаем, что электрон не имеет скорости поступательного движения - пусть, например, он связан в атоме.

На такой простой модели можно хорошо проиллюстрировать многие свойства, связанные с теплотой.

Рассмотрим систему, состоящую из большого числа электронов, закрепленных в разных точках пространства, например, пусть это будет много атомов, каждый из которых содержит электроны. Энергия такой системы в магнитном поле определяется тем, сколько электронов имеют спин, направленный по полю, и сколько - против поля.

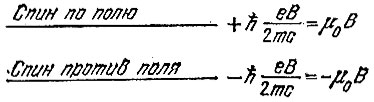
Рис. 18. Энергия электрона в магнитном поле

Если мы условно изобразим два возможных положения спина электрона двумя горизонтальными линиями, написав около них значение энергии (рис. 18), то схему распределения спинов электронов можно будет в дальнейшем изображать кружочками-электронами, нарисованными на этих линиях (мы, конечно, будем рисовать лишь несколько кружочков),

Систему электронов с магнитными моментами можно сравнить с идеальным газом. Роль скоростей атомов, вернее их кинетической энергии здесь играет энергия электрона в магнитном поле. Но кинетическая энергия может принимать любое положительное значение, а энергия в магнитном поле - только два значения.

Замечательно, что это обстоятельство не изменяет основного закона статистики: в тепловом равновесии вероятность найти частицу в состоянии с энергией е пропорциональна экспоненте ехр(- ε/кТ).

Как и в газе, при этом необходимо, чтобы тепловое равновесие атомов между собой могло реально достигаться. Для этого нужно, чтобы атомы идеального газа сталкивались, а магнитные моменты взаимодействовали бы как-то друг с другом. При этом условии закон статистики будет выполняться независимо от того, какой конкретно механизм приводит систему в состояние теплового равновесия.

Из всего, о чем было рассказано, можно заключить, что в тепловом равновесии число электронов п(-1/2), имеющих энергию - μ₀B будет больше, чем число электронов п(+1/2), которые имеют энергию + μ₀В,

Отношение этих двух чисел (их называют населенностями уровней) определяется отношением экспонент:

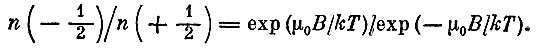
Эта простая формула замечательна тем, что она справедлива для систем из очень большого числа частиц и почти не зависит от того, как система устроена,- надо только, чтобы у системы были состояния с определенной энергией и чтобы существовал какой-либо путь к тепловому равновесию. Тогда ее конечное равновесное состояние будет определяться одним параметром T- ее термодинамической температурой. Такое свойство систем было доказано американским физиком Гиббсом в самом начале XX века.

До открытия квантовой механики физики даже не подозревали, что существуют системы, которые имеют лишь конечное число возможных состояний. Поэтому они не могли представить того огромного количества красивых эффектов, которые связаны с такими простыми системами.