Магнитные стрелки

Пусть вместо электронов с магнитными моментами у нас есть много стрелок от компаса, укрепленных в беспорядке на иголках (рис, 19), Так как магнитным стрелкам положено смотреть на север, то они вначале будут колебаться около направления юг -север. Если бы трение в опоре отсутствовало и если бы стрелки не притягивались друг к другу, то такие их колебания продолжались бы сколь угодно долго. В действительности, конечно, колебания прекратятся, так как их энергия истратится на работу против сил трения в опоре, и все стрелки покажут на север. Кроме того, магнитные стрелки действуют друг на друга, их движения "сцеплены" - они могут передавать друг другу часть своей энергии. Нетрудно увидеть в этом поведении стрелок модель установления равновесия в системе спинов.

Рис. 19. Система магнитных стрелок

Опоры стрелок играют роль холодильника, которому стрелки передают свою кинетическую энергию. Остановившиеся стрелки похожи на систему спинов при температуре T=0^*). Температура "нуль" появилась из-за того, что энергия всегда передается от стрелок к опорам и равновесие может установиться лишь тогда, когда будет передана вся энергия.

^* ( Конечно, стрелки примут температуру комнаты T, а не абсолютного нуля, но и при этом, колебания практически прекращаются.)

Если рассмотреть систему магнитных стрелок более внимательно, то мы выяснили бы, что стрелки не останавливаются окончательно, а под влиянием ударов молекул воздуха и малых колебаний самих опор на самом деле колеблются с очень малой амплитудой, так что их энергия не опускается до нуля, а остается равной (в среднем) кТ. Такое движение называется броуновским. Его теоретическое объяснение было дано Эйнштейном в 1905 г.

Модель электронов в магнитном поле (или магнитных стрелок) полезна для понимания того, что же такое абсолютный нуль температуры.

При любой температуре два возможных направления спина будут встречаться с разной вероятностью. При очень низких температурах почти все электроны будут находиться на нижнем уровне - их спины будут смотреть против поля. Верхний уровень будет практически пустым- не "заселенным". Чем выше температура, тем больше "заселяется" верхний уровень, и, например, при очень высоких температурах (kT>>ε) обе проекции спина будут иметь почти равную вероятность (рис. 20).

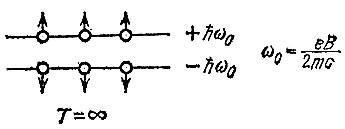
Рис. 20 Равные вероятности заселения уровней (T=∞)

Если температура понижается, то все большая доля электронов будет иметь спицы, направленные против поля. Если Т=0, то против поля окажутся направленными спины всех электронов (рис. 21). Такое состояние системы отвечает абсолютному нулю температуры.

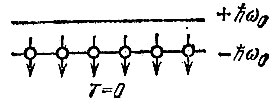
Рис. 21 Все электроны на нижнем уровне (T=0)

В квантовой теории понятие абсолютного нуля приобретает очень четкий смысл. Среди энергетических уровней любой квантовой системы есть один уровень, который обладает наинизшей энергией. В рассмотренном нами примере такое состояние есть состояние, при котором спины всех электронов направлены против поля. При абсолютном нуле система находится в основном состоянии, и поэтому она не может отдавать энергию никакой другой системе просто потому, что у нее нет более низких уровней, на которые она могла бы перейти, потеряв энергию.

Мы говорили, что не очень ясное представление об абсолютном нуле, связанное с законом Гей-Люссака, существовало давно. Но даже в начале века понятие абсолютного нуля еще казалось не вполне ясным. В "Детской энциклопедии", изданной в 1914 г., писали: "Итак, если при охлаждении газ сжимается, то, следовательно, объем его уменьшается. Является вопрос: не будет ли возможным исчезновение его, когда мы доведем газ до состояния абсолютного холода?" Такие высказывания звучат сейчас наивно. Все же удивительно, как много было заключено в простой дроби 1/266" появившейся в эмпирической формуле Гей-Люссака^*.

^* (Напомним, что у Гей-Люссака 1/266 - это неточное значение коэффициента расширения идеального газа (современное значение 1/273,15 К^-1).)