Реальный, необратимый мир

Рассказывая о циклах Карно, мы всегда подчеркивали, что все процессы обратимы. В реальном мире так не бывает. Возьмем, например, сосуд с газом, разделенный на две части теплоизолирующей перегородкой. Предположим, что температура в обеих половинах сосуда разная. Уберем перегородку. Температура начнет выравниваться (вместе с ней выравняется и давление) , Никакой выгоды от такого процесса получить нельзя, разность температур исчезает, а никакой видимой работы не совершается. Нетрудно увидеть и причину такой потери. Процесс теплопроводности, процесс выравнивания температуры необратим - не затратив работы, нельзя вернуть систему в исходное состояние.

С таким "исчезновением" возможной работы мы встречаемся на каждом шагу. Описывая изотермический процесс, при котором тепло переходит от нагревателя к рабочему газу, мы замечали, что этот процесс будет необратим, если между газом и нагревателем будет существовать хоть какая-либо разность температур. Необратимые процессы возникнут и внутри расширяющегося газа, если его температура не будет поддерживаться строго постоянной по всему объему. Поэтому на самом деле цикл Карно осуществить нельзя: для этого надо уничтожить все перепады температур. Но если это сделать, то тепло перестанет перетекать от нагревателя и машина работать не будет.

Что же происходит с газом, в котором протекает необратимый процесс? Рассмотрим опять сосуд с газом, разделенный на две половины, и сосчитаем изменение энтропии газа при выравнивании температур.

Процесс перемешивания газа можно описать так: каждая порция газа расширяется, и ее объем увеличивается в два раза. Будем для простоты считать, что в каждой половине сосуда находилось 1/2 моля таза и что в обеих половинах давление одинаковое. Так как температура после смешивания приняла, очевидно, значение 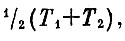то изменение энтропии будет равно

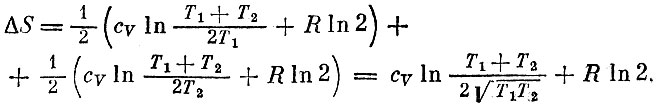
Заметам, что это положительное число, так как (T₁+T₂)²≥4Т₁Т₂. Энтропия возросла. Только в обратимых процессах энтропия системы остается постоянной - потери энтропии одной частью компенсируются выигрышем другой. Энтропия нагревателя уменьшается ровно настолько, насколько увеличивается энтропия рабочего газа, т. е. на ΔQ/Т. Модель теплорода работает хорошо, когда надо описывать передачу теплоты от нагревателя к рабочему газу. Но когда рабочий газ отдает количество теплоты Q₂ холодильнику, то это количество теплоты меньше, чем то, которое он получил от нагревателя. В то же время энтропия ΔQ/Т, передаваемая холодильнику, в точности равна Энтропии, полученной от нагревателя. В обратимом процессе от нагревателя к холодильнику в целости и сохранности передается энтропия, а не количество теплоты.

Если бы это знал Карно, то, наверное, он дальше рассуждал бы так. Если в цикле передается количество Теплорода (предположим, что Карно так назвал бы энтропию), равное Q₁/T₁ умножая эту величину на разность Температур, получим, что работа, произведенная тепловой машиной, равна

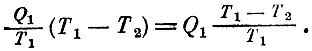
В этой формуле, конечно, мы узнаем выражение для работы идеального цикла с коэффициентом полезного действия

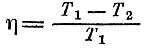
выражение, полученное лишь Клаузиусом спустя много лет после смерти Карно.

И все-таки модель теплорода спасти нам не удается. В необратимых процессах энтропия не сохраняется, и ее никак нельзя в таких процессах отождествлять с теплородом, который, по самому своему смыслу, не должен ни создаваться вновь, ни исчезать бесследно. Так что с теплородом приходится все же распроститься.