Энтропия идеального газа

Хотя энтропию нельзя измерить, ее можно вычислить теоретически. Проще всего это сделать для идеального газа.

Возьмем 1 моль газа при некоторой температуре Т₀. Пусть газ занимает объем V₀. Переведем его в другое состояние со значениями температуры и объема Т и V. Сделаем это в два этапа. Сначала расширим газ изотермически, так, чтобы его объем стал V, а на втором этапе нагреем его при постоянном объеме до температуры Т. На первом этапе газ совершит работу (мы ее вычисляли), равную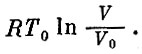

При этом газ получил от нагревателя количество теплоты, равное той же величине. Значит, его энтропия возросла на

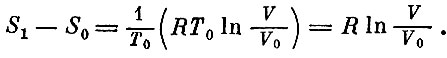
На втором этапе для нагревания газа на величину ΔТ затрачивается количество теплоты, равное c_vΔT. При этом энтропия газа возрастает на

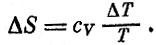
Чтобы сосчитать изменение энтропии, когда температура изменяется на конечную величину от Т₀ до T, нужно просуммировать все вклады ΔS, учитывая, что Т растет. Это нетрудно сделать, если считать, что теплоемкость c_v остается в течение всего процесса постоянной.

Вычисление здесь надо производить по той же схеме, по которой мы вычисляли работу в изотермическом процессе. Для небольшого изменения объема мы писали

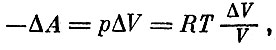
что привело к формуле (при T=const)

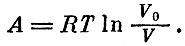
По аналогии мы можем написать и изменение энтропии при изменении температуры от T₀ до T:

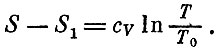
Отсюда уже прямо вытекает формула для полного изменения энтропии:

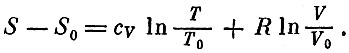
Значения V₀ и Т₀ могут быть выбраны произвольно, поэтому полученная формула позволяет вычислять только изменение энтропии, а не ее абсолютную величину.

Это обстоятельство не должно нас смущать. В любом процессе мы имеем дело только с изменениями энтропии, энергии, и их абсолютные величины не входят в вычисление тепловых процессов. Абсолютная величина энтропии нам понадобилась бы для сравнения энтропии для разных веществ, например для водорода, кислорода и воды, в химической реакции. Такие расчеты научились делать только тогда, когда была установлена связь энтропии со статистикой, с вероятностью.

Но об этом речь будет впереди.