Сопряженные величины

Напишем еще раз формулу для количества теплоты, подводимой в какой-то системе в обратимом процессе:

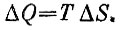
Эта формула напоминает формулу для количества работы, совершаемой над телом:

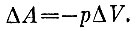
В левых частях обеих формул стоят величины количества теплоты и работы, для которых имеет смысл говорить лишь об их изменении: ΔQ и ΔА имеют вполне четкий физический смысл, но нет величин, которые бы можно было назвать теплотой Q или работой А, содержащимися в теле. Величины Т и р похожи друг на друга: равенство температур и давлений - два условия равновесия, обе величины измеряются непосредственно, Т - термометром, р - манометром.

Естественно ожидать, что должно быть что-то общее и у оставшихся двух величин - энтропии и объема. Одно такое свойство очевидно. Объем любой системы равен сумме объемов ее частей. Точно так же энтропия системы равна сумме энтропий ее частей. Объем и энтропия - величины аддитивные (или, как говорят, экстенсивные, в отличие от температуры и давления - величин интенсивных: Т и р системы равны Т и р любой ее части).

Величины р и V называют сопряженными, также сопряженными величинами являются энтропия S и температура Т.