Формула Больцмана

После Томсона и Нернета здание классической термодинамики было завершено^*. Но к тому времени, когда в термодинамике завершились, так сказать, "отделочные работы", развился новый взгляд на физические явления, взгляд со стороны кинетической теории газов. Надо было соединить в одно целое то, что делал Максвелл, и то, чего достигли Томсон и Нернст. С точки зрения Максвелла газ - это коллектив частиц, каждая из которых описывается уравнением механики Ньютона.

^* (Термодинамика выглядела настолько завершенной, что ученик Гильберта Каратеодори придумал строгое изложение термодинамики (совсем, как в математике), основанное на аксиомах.)

Большим успехом кинетической теории газов было объяснение давления и внутренней энергии. Мост между механикой и термодинамикой выглядел вполне надежным, если бы не одна его слабость - в механике не было места энтропии.

Найти это место оказалось задачей необычайно трудной. Когда она была, наконец, решена в 1872 г. Больцманом, то вновь повторилась старая история: Больцман встретил непонимание большинства своих коллег. Старое поколение не видело причин, которые оправдывали бы пересмотр вполне хорошей теории теплоты.

Больцман увидел, что энтропия появляется в кинетической теории как результат применения понятий теории вероятности к системам, на которые до него смотрели только с точки зрения механики.

Формула, открытая Больцманом, имеет очень простой вид:

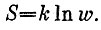
Она связывает термодинамическую величину - энтропию - со статистической величиной ω - вероятностью состояния. Коэффициент k был добавлен в эту формулу позже Планком, который и назвал его постоянной Больцмана. В физике есть короткие формулы, полные глубокого смысла. Они устанавливают связь между величинами, которые раньше считались имеющими совсем разную природу. Так, формула Ньютона 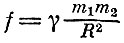установила связь между массой и силой тяготения; формула Эйнштейна Е=тс² объединила два совершенно разных в классической механике понятия - массу и энергию; формула Планка ћω=ε открыла связь между частотой и энергией кванта; формула Хаббла v=HR - связь между расстоянием до галактик и скоростью их разбегания. Это все великие формулы, и формула Больцмана занимает среди них почетное место, а сам Больцман остался в истории как один из главных создателей статистической физики.

Чтобы понять смысл формулы Больцмана, рассмотрим сосуд объемом V₀, в котором находится идеальный газ. Атомы газа беспорядочно движутся внутри сосуда. С течением времени каждый атом побывает одинаково часто (с одинаковой вероятностью) практически во всех частях сосуда. Не делая большой ошибки, можно сказать, что половину всего времени каждый атом проводит в правой, а половину времени в левой половине сосуда. Также можно утверждать, что если сосуд мысленно разделен на четыре равные части, то в каждой из них атом проводит одну четверть всего времени. Продолжая эти рассуждения, можно заключить, что в каждом выделенном объеме V (независимо от его формы) атом проводит долю времени, равную V/V₀, если V₀ - объем всего сосуда. Этот факт можно описать так: вероятность найти атом в объеме V равна ω=V/V₀.

Соберем теперь все интервалы времени, когда наш атом (мы обозначим его атом 1) находится в объеме V, и будем следить за другим атомом - атомом 2. Этому атому нет никакого дела до поведения и местонахождения атома 2. Поэтому независимо от того, где находится атом 1, атом 2 долю времени V/V₀ также проводит в объеме V. Это значит, что за некоторое большое время т атом 1 будет находиться в объеме V в течение времени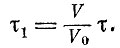
. За это же время τ_t атом 2 будет находиться в том же объеме V в течение времени

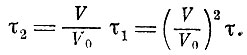
Отсюда можно заключить, что вероятность найти в объеме V атом 1 и 2 вместе равна ω₂=(V/V₀)². Это рассуждение можно продолжить, включив в него и другие атомы.

Таким образом, вероятность найти в объеме V все N_A атомов (весь моль) равна

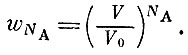
Эта вероятность относится к такому странному состоянию, когда газ, заполняющий весь сосуд, случайно сожмется и займет объем V. Постоянная Авогадро N_A невообразимо велика, поэтому ω_NA очень мала: никогда не бывает, чтобы газ сам очистил хотя бы самую незначительную долю объема, т. е. чтобы V отличалось от V₀ на сколько-нибудь заметную величину.

Если мы теперь сравним формулу для вероятности с выражением для энтропии идеального газа (при T=T₀)

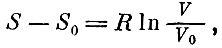
или, для одной молекулы,

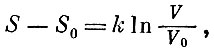
то увидим, что^*

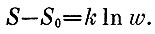
Это и есть формула Больцмана для идеального газа при T=const.

^* (На самом деле мы вычисляем не саму энтропию, а ее приращение при переходе от объема V₀ к объему V. Энтропия исходного состояния газа (температура T₀, объем V₀) остается неопределенной постоянной. Это относится и ко всем дальнейшим формулам. )