Как зависит S от температуры?

Доказательство формулы Больцмана для газа, в котором меняется температура, существенно более сложно. Мы приведем не вполне строгое рассуждение.

Для этого вспомним, что мы говорили в связи с распределением скоростей Максвелла. Будем следить за тем, как движутся атомы в пространстве скоростей, т. е. как изменяется скорость атомов со временем. В отличие от обычного пространства, пространства координат, в котором атом мог находиться в любой точке с равной вероятностью, в пространстве скоростей его "координаты" v принимают лишь значения, близкие к среднему значению скорости:

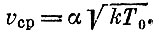
Мы не будем уточнять, о какой средней скорости идет речь - среднеквадратической, наиболее вероятной и т. д., и оставим коэффициент α без внимания. Скорость атомов, как это следует из распределения Максвелла, не равна точно v_cp. Но можно сказать, что большая часть атомов имеет скорость, которая отличается от v_cp не более чем на

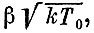
где β - еще одна постоянная, точный смысл которой нам не важен.

Такое утверждение можно оправдать, если вспомнить, что говорилось о дисперсии - разбросе значений v² (или энергии) около среднего значения (строгое обоснование его сложно). Можно сказать, что в пространстве скоростей подавляющая часть молекул оказывается в объеме, все точки которого находятся на расстоянии, не большем, чем примерно

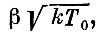
от точки, отвечающей значению компонент средней скорости.

Теперь можно сказать, что в пространстве скоростей почти все атомы находятся в объеме, примерно равном β³ (kT₀)^3/2. Если температура газа изменилась до значения T, то этому изменению в пространстве скоростей отвечает картина, в которой почти все атомы "столпились" в меньшем объеме, если Т <Т₁ или "разбежались" в больший объем, если Т >Т₀.

Вычислить вероятность такого события совсем просто. Надо действовать так же, как действовали мы при вычислении вероятности "собирания" газа в меньший объем в обычном пространстве. Вероятность эта равна

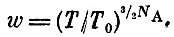
Заметьте, что коэффициенты αи β исчезли из формулы - потому-то мы не стали ими интересоваться.

Энтропия равна логарифму этого выражения, умноженному на R. Значит,

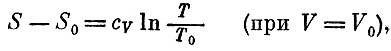
так как c_v=3/2N_Ak есть теплоемкость 1 моля одноатомного газа при постоянном объеме.

Выведенная формула совпадает с той, которая была получена из термодинамики. Однако если сравнить этот вывод со старым выводом, в котором вычислялось количество теплоты и работа и совсем не упоминалась вероятность, то приходится удивляться, сколь разные точки зрения в физике приводят в конце концов к одним и тем же формулам. Возможность смотреть на физические явления с самых разных точек зрения - характерное свойство современной науки. Научиться этому; - первейшая задача естествоиспытателя.