Плотность состояний

Совсем по-другому появляются энтропия и температура в системах, в которых действую законы квантовой механики. В таких системах, как, например, атомное ядро, нельзя измерять у частиц (нуклонов) их координаты и скорости. Да это и никому не нужно. Атомное ядро характеризуется тем, какие значения энергии оно может иметь^*,- эти значения энергии составляет то, что называют спектром атомного ядра.

^* (Каждое состояние ядра, кроме энергии, описывается еще рядом других характеристик: спином, четностью и т. д. О них мы подробно говорить не будем, но они важны, так как может быть много состояний с одной энергией, отличающихся другими характеристиками.)

Если атомное ядро получило извне большую энергию, например, оно захватило нейтрон, то после такого акта захвата оно с примерно равной вероятностью может оказаться в одном из многих "конечных" состояний. Объем ядра почти не изменяется, поэтому свобода выбора конечного состояния ограничивается выбором энергии. Задача становится похожей на задачу вычисления вероятности в пространстве скоростей. Однако в случае ядра мы ничего не знаем о скоростях нуклонов. Зато мы знаем, что у ядра есть много уровней энергии. В каждом маленьком интервале энергии (если сама энергия не очень мала) расположено сравнительно много уровней, и мы можем говорить о числе уровней Δn на единичный интервал энергии ΔЕ. Такую величину Δп/ΔЕ называют плотностью состояний и обозначают р(E) Можно высказать такую гипотезу: вероятность найти ядро (после захвата нейтрона) в некотором состоянии пропорциональна плотности состояний в том интервале энергии, в который попадает ядро по закону сохранения энергии.

Если выбрать какую-то плотность состояния за стандартную, эталонную р₀, и относить плотности состояний к этой произвольно выбранной единице, то для энтропии получим по формуле Больцмана

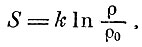
Такой грубой формулой можно пользоваться для приближенного описания систем с достаточно большим числом степеней свободы. Она нашла, например, красивое применение для описания ядерных реакций.