Температура атомных ядер

В 1937 г. Бор предложил описывать ядерные реакции с помощью модели составного, или "компаунд"- ядра. Идея этой модели состояла в том, что реакция, которая происходит при столкновении нейтрона с ядром, описывается в два этапа. Первый этап состоит в захвате нейтрона ядром. Если энергия нейтрона не велика, то он быстро растрачивает ее. Нейтрон притягивается ядром, и эта энергия притяжения "разбазаривается" между нуклонами, так что внутри ядра устанавливается некоторое статистическое распределение. Чем больше энергии попадает в ядро, тем больше оно "возбуждается" и попадает в область, характеризующуюся высокой плотностью состояний, которая очень быстро растет с энергией возбуждения.

В таком состоянии ядро оставаться долго не может. Подобно нагретой жидкой капле, ядро должно отдать избыточную энергию и охладиться. Излишек энергии будут уносить "испаряющиеся" частицы.

Этот процесс может быть описан аналогично испарению с поверхности нагретой капли. Испаряющиеся молекулы распределяются по Максвеллу, с тем только отличием, что распределение здесь описывает не покоящийся (как целое) газ, а поток^* молекул, вытекающих из жидкости. Чтобы описать процесс испарения частиц из ядра, надо знать температуру ядра. Но мы знаем только энергию возбуждения и плотность уровней - температуру же ядра мы измерить не можем. Ни один из приборов, известных термометристам, даже в принципе не подходит для выполнения такой задачи. Зато температуру ядра можно вычислить.

^* (В таком распределении появляется лишний множитель v_z (z - нормаль к поверхности), учитывающий тот факт, что поток частиц пропорционален произведению их плотности на компоненту их скорости.)

Если немного возбудить ядро, добавив ему энергию ΔЕ, то его энтропия возрастет на

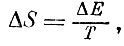
так как увеличение энергии ядра и подвод тепла к ядру - это одно и то же, Подставляя сюда значение ΔS, получим

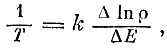
т. е. обратная температура равна скорости изменения логарифма плотности состояний с энергией возбуждения. Чем сильнее возбуждение, тем больше плотность состояний и тем больше температура ядра.

^* (Здесь учтено, что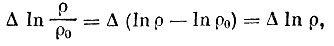 поскольку p₀=const и ΔInр₀=0.)

Написанная формула кажется не похожей на те формулы, с которыми мы имели дело раньше. И действительно, говоря об атомном ядре как квантовой системе, мы описываем его возможные состояния как систему отдельных дискретных уровней. При описании же идеального газа, например, его состояние характеризовалось скоростями молекул. Только этим и объясняется различие в формулах. Формула для энтропии идеального газа выводилась из вероятностей найти N частиц в одном и том же объеме пространства скоростей. Чтобы получить формулу, которая была только что получена для ядра, оценим объем, который занимает газ в пространстве скоростей. Обозначим среднюю скорость молекул газа через v_ср. Как и раньше, не имеет значения, какая это скорость - средняя, наиболее вероятная или средняя квадратическая: все они отличаются лишь численным коэффициентом, который не играет роли при выводе. Тогда интересующий нас объем представляет собой шаровой слой, сосредоточенный около сферы с радиусом v_ср. Толщина такого слоя равна, очевидно, ширине распределения Максвелла, которая, как мы знаем, пропорциональна корню квадратному из температуры (kТ)^1/2 или, что то же, пропорциональна той же средней скорости v_cp. Таким образом, объем шарового слоя О оказывается равен O= αv³, при этом численное значение а нас не интересует. Эту формулу можно интерпретировать и как объем шара. Формулы, связанные с вероятностями для систем из очень многих частиц, обладают замечательной особенностью не требовать для себя слишком точного определения. Так, в нашем случае не существенно, о чем говорить, об объеме шара, или об объеме шарового слоя, или даже об объеме куба со стороной v_cp. Это свойство когда-то очень удивило физиков, и для него было придумано специальное название - нечувствительность энтропии. Теперь можно утверждать, что вероятность найти N молекул в объеме Ω равна

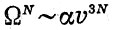
(опять мы опускаем коэффициент). По определению энтропия

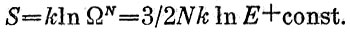
В const включен вклад от опущенных факторов. Эту формулу можно переписать теперь так:

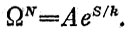
Здесь А - постоянный множитель. Мы видим, что роль плотности уровней играет объем Ω^N. Этим и устанавливается соответствие между старыми и новыми формулами.

Температуру ядра естественно измерять не в кельвинах, а в энергетических единицах, т. е. в джоулях, избавившись, наконец, от постоянной Больцмана k. Однако джоуль - единица слишком большая, поэтому температуру (так же, как и энергию возбуждения ядра) принято измерять в миллионах электрон-вольт: 1 МэВ=1,6-10^-13 Дж или 1 МэВ=10¹⁰ К.

Конечно, применение к ядру понятия температуры не очень обосновано. Число частиц в ядре невелико, и ядро не забывает полностью свою историю. Тем не менее во многих случаях спектр скоростей нейтронов, вылетающих из возбужденного ядра, очень похож на спектр молекул, испаряющихся из нагретой капли. Только температура, которой отвечает распределение частиц, очень большая. Можно показать, что температура ядра растет примерно как корень квадратный из энергии возбуждения и составляет (в энергетических единицах) примерно 1-1,5 МэВ при энергии возбуждения 10 МэВ в области ядер с А≈100. Это соответствует приблизительно 10¹⁰ К, так что нейтронный "пар" над ядром на самом деле очень горячий!

Пример с температурой ядра интересен для нас еще и тем, что в ядре в единицах энергии измеряют две величины - величину возбуждения и температуру, показывающую, как изменяется плотность уровней с ростом энергии возбуждения. Именно это различие между количеством теплоты и температурой трудно было понять нашим предкам.